
Dérivation partie 1
Je me teste avec des QCM
Exercices par niveau
Vers l'épreuve écrite
Maîtrisez les méthodes essentielles
Vérifiez et consolidez vos compétences avec notre collection de méthodes fondamentales du cours.
Méthodes disponibles
5 méthodes
Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire
Logarithmes
La fonction réciproque de la fonction exponentielle $y=e^x$ s'appelle la fonction logarithme népèrien et est définie par: $$\begin{cases} x\mapsto ln(x) \newline ]0;~+\infin[ \to \R \end{cases}$$
Pour tout nombre $a>0$, la fonction logarithme népèrien de $a$ l'unique solution réelle de l'équation $e^x=a$
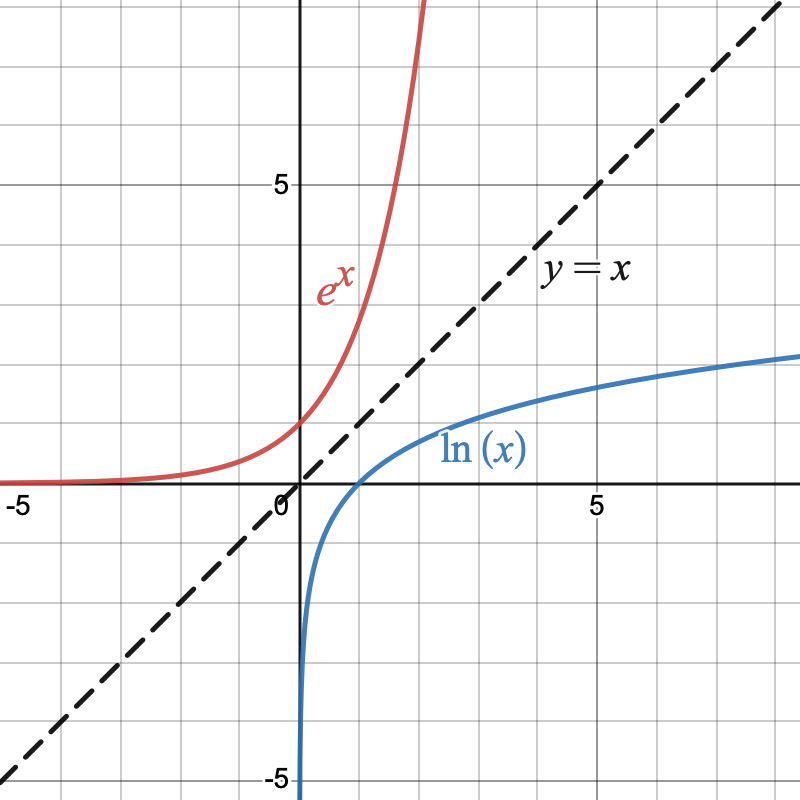
- Pour tout $x\in ]0;~+\infin[$, on a $e^{ln(x)}=x$
- Pour tout $x\in \R$, on a $ln(e^x)=x$
Contenu Premium Verrouillé
Abonnez-vous pour accéder à cette fiche et bien plus encore
Commencer mon abonnementPrêt pour t'entraîner avec les sujets de bac ?
Teste tes connaissances avec les sujets du baccalauréat les plus récents




