Contrôles d'entraînement
sur 1 exercice complété
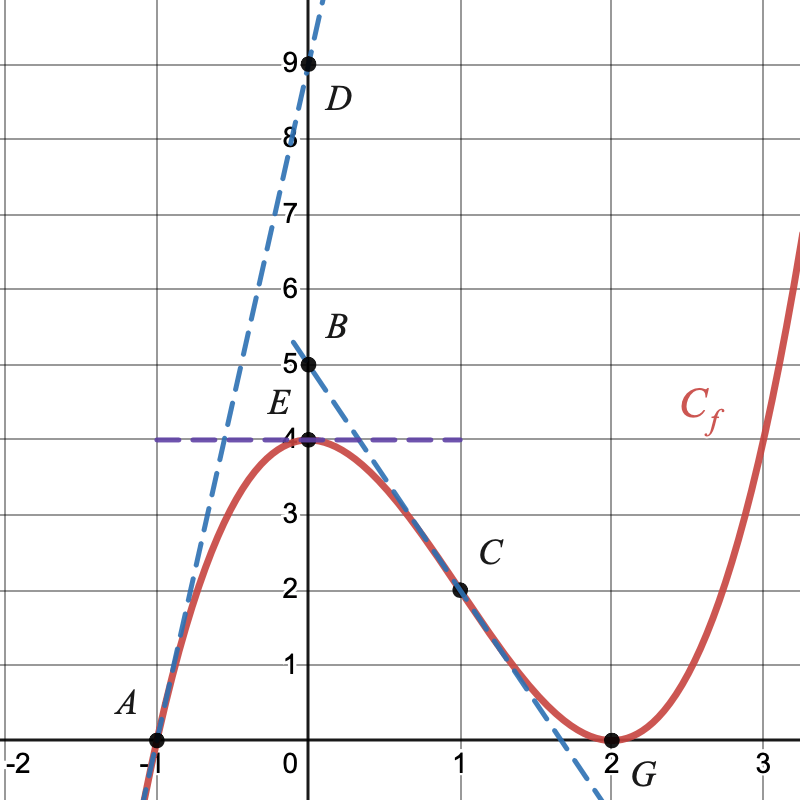
On considère la fonction $f$ de courbe représentative $C_f$. Sur la figure sont représentés:
- Les points $A(-1;~0)$, $E(0;~4)$, $B(0;~5)$, $C(1;~2)$, $G(2;~0)$.
- La tangente $(AD)$ à $C_f$ au point $A$.
- La tangente $(BC)$ à $C_f$ au point $C$.
- Déterminer graphiquement les valeurs de $f'(-1)$, $f'(0)$, $f'(1)$ et $f'(2)$.
- En déduire grapiquement les équations des tangentes $(AD)$ et $BC)$.
- Déterminer graphiquement le tableau de variations de la fonction $f$ sur $\R$.
- Retrouver par le calcul les équations réduites des tangentes $(AD)$ et $BC)$.
- Montrer que l'équation $f'(x)=0$ admet exactement 2 solutions.
- La courbe $C_f$ admet-elle des tangentes parallèles à la droite d'équations $y=24x-3$? Si oui donner leurs équations.
L'équation de cette fonction est $f(x)=x^3-3x^2+4$.
Déterminer le l'ensemble de dérivabilité des fonctions suivantes puis calculer leur dérivée
- $f(x)=\dfrac{3}{4}x^4-7x^3+\dfrac{2}{x}$
- $g(x)=\sqrt{3x-1}$
- $h(x)=(4x^2-5)(x^3-x-1)$
- $j(x)=\dfrac{x+1}{x^2-1}$
- $k(x)=\sqrt{x}(3x+5)$
- $l(x)=(7-5x)^2$
Soit $f$ la fonction définie sur $\R^*$ par:$$f(x)=3x+\dfrac{5}{x}+2$$
- Déterminer l'expression de $f'(x)$, la fonction dérivée de $f$.
- La courbe représentative de $f$ admet-elle des tangentes horizontales? Si oui, pour quelles valeurs de $x$?
- Déterminer l'équation réduite de la tangente à la courbe $C_f$ au point d'abscisse $-2$.
- La courbe $C_f$ admet-elle une tangente parallèle à la droite d'équation $y=-2x+3$? Si oui, en quel(s) point(s)?
- Montrer que pour tout nombre réel $a$ non nul, une équation de la tangente à la courbe de $f$ en $a$ est: $$y=\Big( 3-\dfrac{5}{a^2} \Big) x + \dfrac{10}{a}+2$$
- Montrer que $C_f$ admet 2 tangentes passant par le point de coordonnées $(3;~6)$ et donner les équations de ces tangentes.
Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire
Dérivation partie 1
Fiche de synthèse
Logarithmes
La fonction réciproque de la fonction exponentielle $y=e^x$ s'appelle la fonction logarithme népèrien et est définie par: $$\begin{cases} x\mapsto ln(x) \newline ]0;~+\infin[ \to \R \end{cases}$$
Pour tout nombre $a>0$, la fonction logarithme népèrien de $a$ l'unique solution réelle de l'équation $e^x=a$
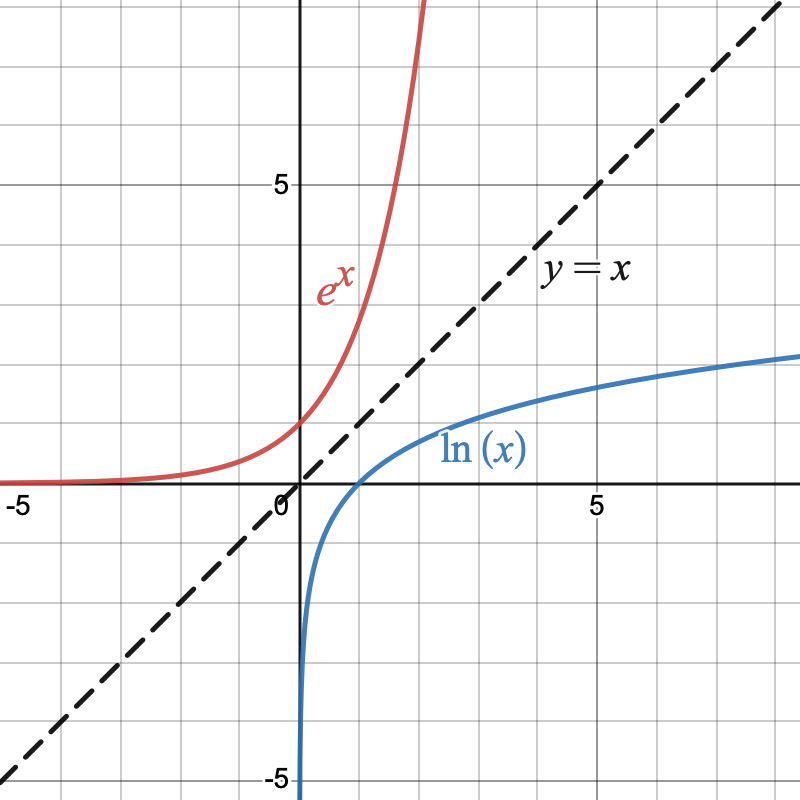
- Pour tout $x\in ]0;~+\infin[$, on a $e^{ln(x)}=x$
- Pour tout $x\in \R$, on a $ln(e^x)=x$
Contenu Complet Premium
Pour accéder au contenu complet de cette fiche de cours, vous devez vous abonner à notre offre premium.
Avec l'abonnement premium :
- Fiches de cours complètes
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Vidéos explicatives détaillées


