ABCDEFGH est un cube d'arrête 1. On se place dans la base $(B,~\overrightarrow{BC},~\overrightarrow{BH},~\overrightarrow{BA})$

Tracer la section du cube ABCEDFGH par le plan (IJK)

On se place dans un repère $(O;\vec{i};\vec{j};\vec{k})$

On considère la représentation paramétrique: $$\begin{cases}x=-1+t\\ y=2-t\\ z=3+t\end{cases}$$

On note $d'$ la droite passant par le point $B(4;4;-6)$ et de vecteur directeur $\vec{u}(5;2;-9)$.

1. Déterminer une représentation paramétrique de la droite $d'$
2. Déterminer si les droites sont sécantes

On se place dans un repère $(O;\vec{i};\vec{j};\vec{k})$

1. Les vecteurs $\vec{u}=\vec{i}-\vec{j}$, $\vec{v}=\vec{i}+2\vec{j}-\vec{k}$ et $\vec{w}=3\vec{j}+2\vec{k}$ sont-ils linéairement indépendants?
2. Les vecteurs $\vec{u}=2\vec{i}+\vec{k}$, $\vec{v}=-\vec{i}+3\vec{j}+\vec{k}$ et $\vec{w}=3\vec{j}-\vec{k}$ forment-ils une base de l'espace?

On considère les vecteurs $\vec{u}(2;-3;1)$ et $\vec{v}(-1;5;3)$

1. Ces vecteurs définissent-ils un plan? Justifier.

On considère le point $A(1,1,3)$ et le plan $(A,\vec{u}, \vec{v})$

2. Le point $B(2,4,8)$ appartient-il au plan?

ABCDEFGH est un cube dans lequel les points $I$, $J$, $K$ sont définis par:

1. $I$ est le milieu du segment $[AD]$
2. $J$ est tel que $\vec{AJ}=\frac{3}{4} \vec{AE}$
3. $K$ est le milieu du segment $[FG]$

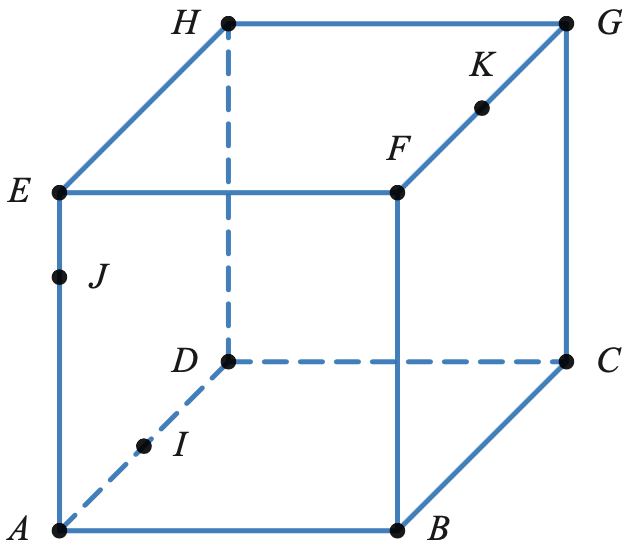
1. Construire le point d’intersection $P$ du plan $(IJK)$ et de la droite $(EH)$.
2. En déduire, en justifiant,l’intersection du plan $(IJK)$ et du plan $(EFG)$.