Soit les points $A(-1;3;2)$, $B(2;-5;0)$ et $C(-4;11;3)$

1. Déterminer les coordonnées des vecteurs $\overrightarrow{AB}$, $-2\overrightarrow{CA}$ et $3\overrightarrow{BA}-2\overrightarrow{CB}$
2. $\overrightarrow{AB}$ et $\overrightarrow{AC}$ sont-ils colinéaires?
3. Que peut-on en déduire pour les points $A$, $B$ et $C$?

ABCDEFGH est un cube d'arrête 1. On se place dans la base $(B,\overrightarrow{BC},\overrightarrow{BH},\overrightarrow{BA})$

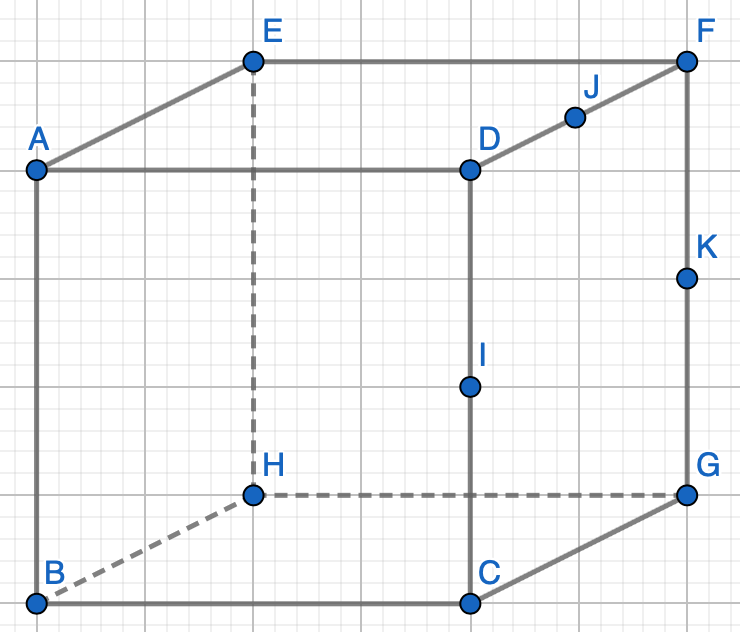
1. Déterminer les coordoonées des points $E$, $I$, $J$, $K$, $G$.
2. Prouver que $\overrightarrow{BI}=\overrightarrow{HK}$
3. Déterminer les coordoonées du point $L$ tel que $EFLJ$ soit un parallélogramme.

Dans la base $(\vec{i},\vec{j},\vec{k})$ on considère les vecteurs:

1. $\vec{u}=-\vec{i}+2\vec{k}$
2. $\vec{v}=-2\vec{j}+3\vec{k}$
3. $\vec{w}=3\vec{i}-\vec{j}$

Déterminer si $\vec{u}$, $\vec{v}$ et $\vec{w}$ forment une base de l'espace.

Soit les points $A(3;-2;1)$, $B(3;1;1)$ et $C(0;-1;-1)$

Déterminer si ces 3 points définissent un plan

On se place dans un repère $(O;\vec{i};\vec{j};\vec{k})$

1. On considère la représentation paramétrique: $$\begin{cases}x=-4t+1\\ y=5t+3\\ z=2t+7\end{cases}$$
1. Donner un vecteur directeur de cette droite
2. Le point $D(-3;\frac{11}{2};8)$ appartient-il à la droite?
3. Déterminer un point qui appartient à la droite
2. Donner une représentation paramétrique de la droite $(AB)$ avec $A(3;5;-1)$ et $B(2;0;7)$.