Les exercices
sur 6 exercices complétés
Calculer les dérivées des fonctions composées suivantes:
- $f$ définie sur $\R$ par $f(x)=\sqrt{x^3-4x^2+3x+1}$
- $g$ définie sur $\R$ par $g(x)=(3e^x+5x^2-1)^4$
- $h$ définie sur $\R \backslash \{3\}$ par $h(x)=e^{\frac{x+1}{x-3}}$
- $k$ définie sur $\R$ par $k(x)=\frac{5}{x^2+x+1}$
On considère la fonction $f$ définie sur $\R$ par $f(x)=2x^3-8x^2+10x-15$
- Étudier les variations de $f$ sur $\R$
- Étudier la convexité de $f$ sur $\R$
- Déterminer les coordonnées des éventuels points d'inflexion
On considère une fonction $f$ définie et dérivable sur $[0;60]$ dont la courbe est donnée ci-dessous.
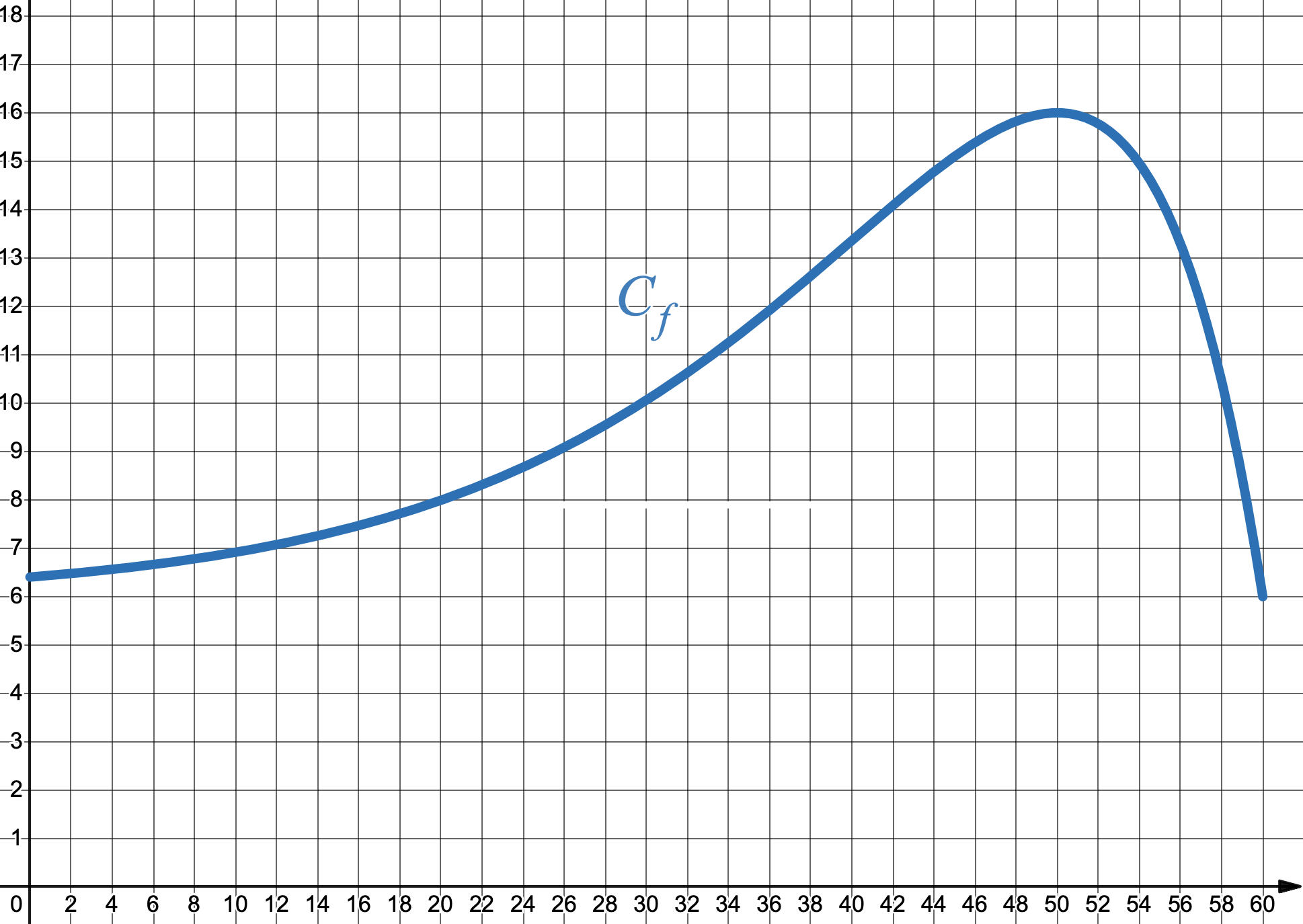
- En argumentant la réponse, donner le signe de $f'(54)$, où $f'$ est la fonction dérivée de $f$.
- Déterminer graphiquement un intervalle sur lequel la fonction $f$ est convexe.
- Calculer $f'$ puis $f''(x)$ et vérifier les résultats des questions précédentes.
$f$ est définie sur $[0;60]$ par $f(x)=6+(60-x)e^{0,1x-5}.$
On considère la fonction $f$ définie sur $\R$ par $f(x)=(-5x^2+5)e^x$
- Montrer que $f'(x)=(-5x^2-10x+5)e^x$ et dresser le tableau de variations de $f$
- Montrer que $f''(x)=-(5x^2+20x+5)e^x$
- Étudier la convexité de $f$ sur $\R$ en précisant les éventuels point d'inflexion.
Calculer les dérivées des fonctions composées suivantes:
- $f$ définie sur $\R$ par $f(x)=e^{x^2-3}$
- $g$ définie sur $\R^+$ par $g(x)=\sqrt{x^2+\sqrt{x}}$
- $h$ définie sur $\R \backslash \{1\}$ par $h(x)=(\dfrac{2x+4}{x-1})^2$
- $k$ définie sur $\R$ par $k(x)=\sqrt{e^{2x}+3x^2}$
$f$ est dérivable sur $[0;15]$ et sa dérivée $f'$ est continue sur $[0;15]$. Les variations de $f'$ sont représentées dans le tableau suivant.
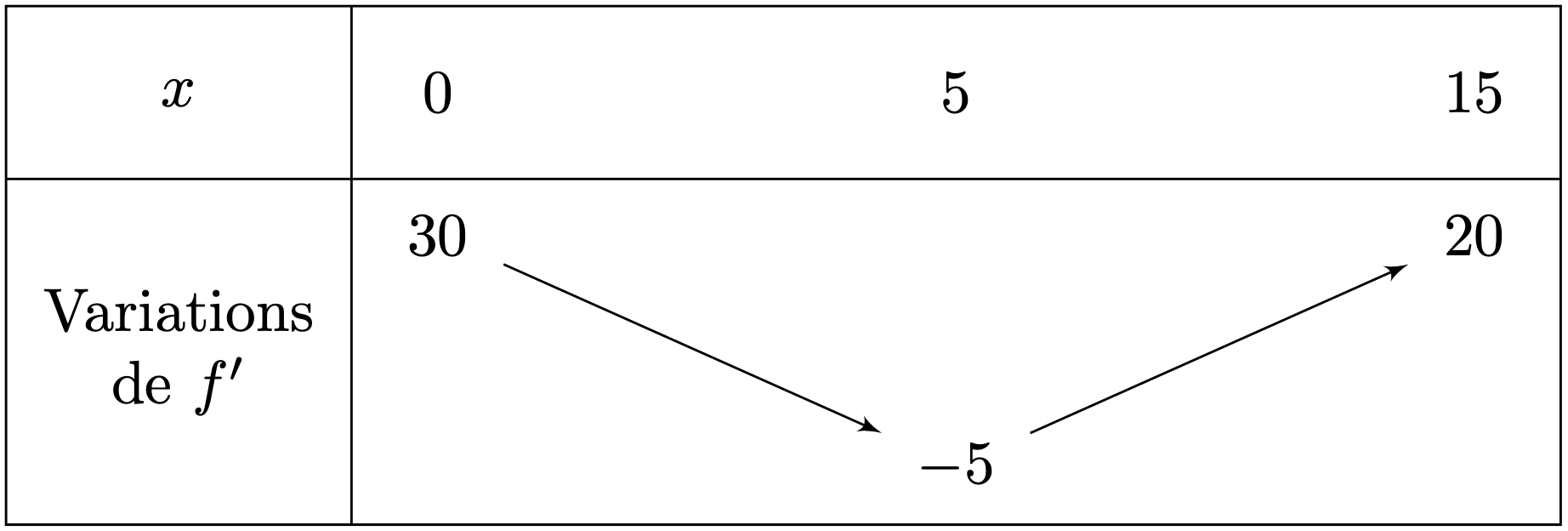
- $C_f$ admet-elle des tangentes parallèlès horizontales? Justifier.
- Déterminer la convexité de $f$ sur $\R$.
- En déduire les potentiels points d'inflexion de $f$
Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire
Dérivation et convexité
Fiche de synthèse
Compléments sur la dérivation
| Condition | Formule |
| $u$ est dérivable sur $I$, $n \in \Z$ n si $n<0$, $u$ ne doit pas s'annuler |
$(u^n)'=n\times u^{n-1}\times u'$ |
| $u$ est dérivable et ne s'annule pas sur $I$ | $(\dfrac{1}{u})'=\dfrac{-1}{u^2}$ |
| $u$ est strictement positive et dérivable sur un intervalle $I$ | $(\sqrt{u})'=\dfrac{u'}{2\sqrt{u}}$ |
| $u$ est dérivable sur un intervalle $I$ | $(e^{u})'=u'\times e^u$ |
Contenu Complet Premium
Pour accéder au contenu complet de cette fiche de cours, vous devez vous abonner à notre offre premium.
Avec l'abonnement premium :
- Fiches de cours complètes
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Vidéos explicatives détaillées


