Les exercices
sur 4 exercices complétés
On considère la fonction $f$ définie pour tout réel $x$ par: $$f(x)=e^{-2x^2+4x-\frac{3}{2}}$$
- Dresser le tableau de variations de $f$ sur $\R$
- Montrer que pour tout réel $x$:$$f''(x)=(16x^2-32x+12)e^{-2x^2+4x-\frac{3}{2}}$$
- Étudier la convexité de $f$ sur $\R$ et déterminer les potentiels points d'inflexion.
$C_1$, $C_2$, $C_3$ sont respectivement les courbes de $f$, $f'$ et $f''$, avec $f$ une fonction définie sur $\R$.
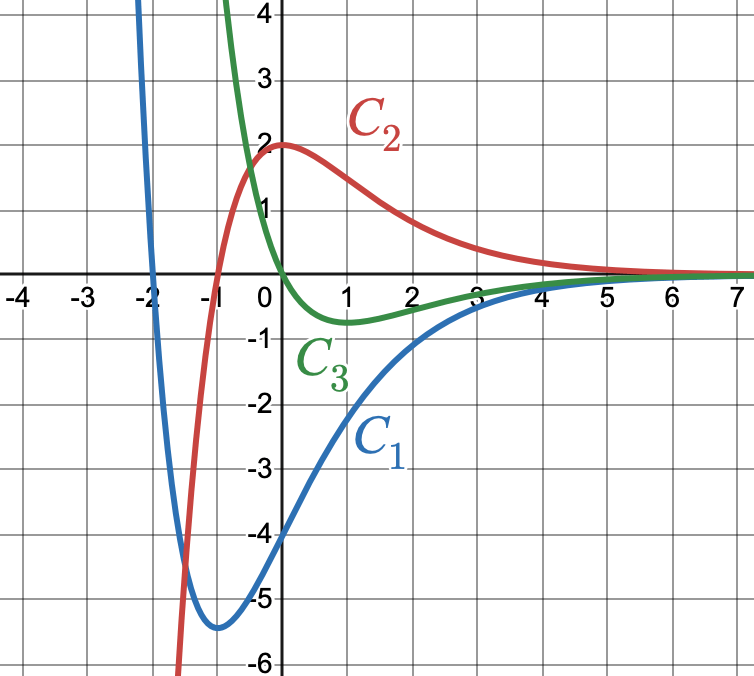
- Dresser le tableau de variations de $f$.
- Déterminer la convexité de $f$ sur $\R$.
- En déduire les potentiels points d'inflexion de $f$
Soit $f$ une fonction deux fois dérivable sur un intervalle $I$. On veut montrer l'implication suivante: pour tout $x\in I$, $f''(x)\geq 0$ $\implies$ $f$ est au dessus de ses tangentes sur $i$.
- Rappeler l'équation réduite de la tangente à $C_f$ en un point d'abscisse $a\in I$
- Soit $g$ la fonction définie sur $I$ par $g(x)=f(x)-f'(a)x+af'(a)-f(a)$. Calculer $g'(x)$ puis $g''(x)$.
- En déduire le signe de $g''(x)$, puis celui de $g'(x)$ et enfin celui de $g(x)$ sur $I$.
- Conclure
On appelle fonction "satisfaction" toute fonction dérivable qui prend ses valeurs entre 0 et 100.
- Il y a "saturation" quand la fonction atteint la valeur 100
- La fonction "envie" est la dérivée de la fonction "satisfaction"
- Il y a "souhait" lorsque la fonction "envie" est positive ou nulle
- Il y a "rejet" lorsque la fonction "envie" est strictement négative
PARTIE A
Le directeur d'une agence de trekking modélise la satisfaction de ses clients en fonction de la durée de leur séjour. On admet que la fonction satisfaction $g$ est définie sur $[0;30]$ par $$g(x)=12,5xe^{-0,125x+1}$$ avec $x$ exprimé en jours.
- Démontrer que pour tout $x\in [0;30]$ $$g'(x)=(12,5-1,5625x)e^{-0,125x+1}$$
- Etudier le signe de $g'(x)$ sur $[0;30]$ puis dresser le tableau de variations de $g$ sur cet intervalle.
- Quelle durée de séjour correspond-elle à l'effet «saturation»?
PARTIE B
La direction des ressources humaines d'une entreprise modélise la satisfaction d'un salarié en fonction du salaire annuel qu'il perçoit. On admet que la fonction « satisfaction » $h$, est définie sur l'intervalle $[10; 50]$ par $$h(x)=\dfrac{90}{1+e^{-0,25x+6}}$$
($x$ est exprimé en millier d'euros).
La courbe $C_h$ de la fonction $h$ est représentée ci-dessous:
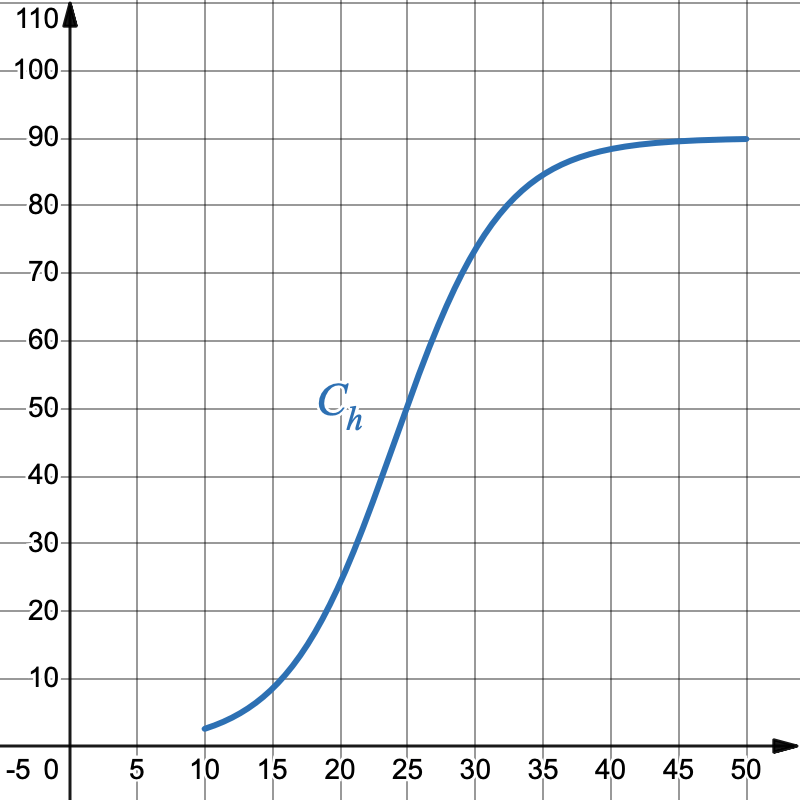
- Conjecturer graphiquement la convexité de $h$ sur l'intervalle $[10; 50]$ ainsi que les potentiels points d'inflexion.
- Calculer la satisfaction correspondant à un salaire de 50 000 euros.
- Déterminer la limite de $h$ quand $x$ tend vers $+\infin$. Que peut-on en déduire sur la saturation dans ce modèle?
- Résoudre dans l'intervalle $[10; 50]$ l'inéquation $e^{-0,25x+6}-1>0$.
- Démontrer que pour tout $x\in [10; 50]$ $h'(x)=\dfrac{22,5e^{-0,25x+6}}{(1+e^{-0,25x+6})^2}$ puis que: $$h''(x)=\dfrac{5,625e^{-0,25x+6}(e^{-0,25x+6}-1)}{(1+e^{-0,25x+6})^3}$$
- En déduire la convexité de $h$ sur l'intervalle $[0;50]$.
- À partir de quel salaire annuel la fonction «envie» décroît? Justifier.
Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire
Dérivation et convexité
Fiche de synthèse
Compléments sur la dérivation
| Condition | Formule |
| $u$ est dérivable sur $I$, $n \in \Z$ n si $n<0$, $u$ ne doit pas s'annuler |
$(u^n)'=n\times u^{n-1}\times u'$ |
| $u$ est dérivable et ne s'annule pas sur $I$ | $(\dfrac{1}{u})'=\dfrac{-1}{u^2}$ |
| $u$ est strictement positive et dérivable sur un intervalle $I$ | $(\sqrt{u})'=\dfrac{u'}{2\sqrt{u}}$ |
| $u$ est dérivable sur un intervalle $I$ | $(e^{u})'=u'\times e^u$ |
Contenu Complet Premium
Pour accéder au contenu complet de cette fiche de cours, vous devez vous abonner à notre offre premium.
Avec l'abonnement premium :
- Fiches de cours complètes
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Vidéos explicatives détaillées


