Les exercices
sur 6 exercices complétés
Préciser si les affirmation suivantes sont vraies ou fausses:
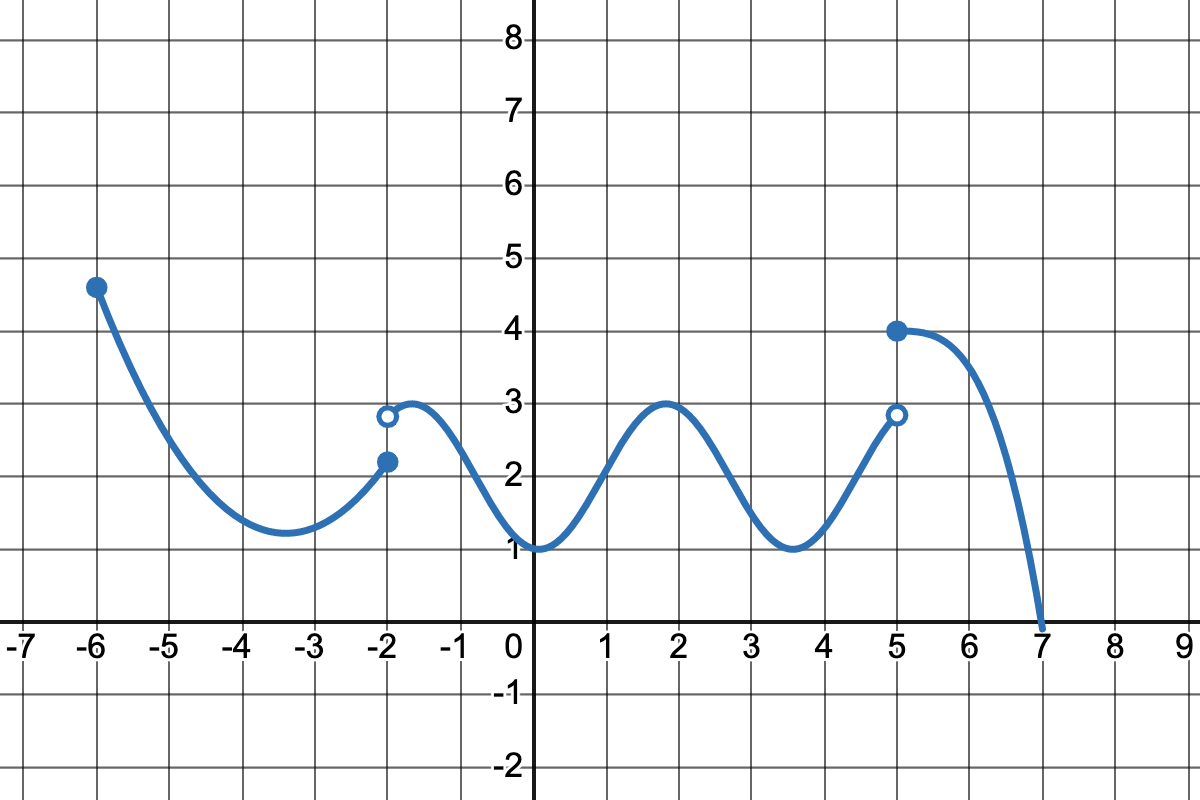
- $f$ est continue en 2
- $f$ est discontinue en -1
- $f$ est continue sur l'intervalle $[-2;2[$
- $f$ est continue sur l'intervalle $]-1;3]$
- $f$ est continue sur l'intervalle $[0;5[$
Étudier la continuité des fonctions suivantes:
- $\begin{cases}\dfrac{x^2+1}{(x-1)^2} &\text{si } x<0\\ -2x+1 &\text{si } x\geq 0\end{cases}$
- $\begin{cases}x^3-12 &\text{si } x<3\\ 7x-6 &\text{si } 3\leq x < 5 \\ x^2-10 &\text{si } x\geq 5 \end{cases}$
- $\begin{cases}-2x^4 &\text{si } x<1\\ x^2+x+1 &\text{si } x\geq 1\end{cases}$
On désigne par $f$ une fonction définie et continue sur $\R$ dont le tableau de variations est donné ci-dessous. Donner le nombre de solutions de chacune des équations suivantes sur l'intervalle précisé.
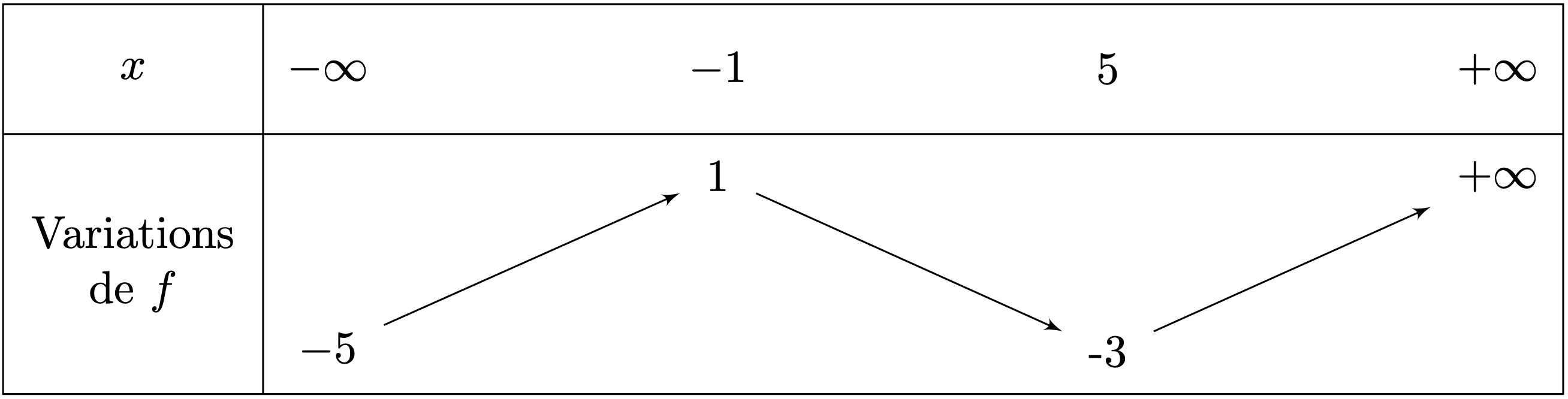
- $f(x)=3$ sur $[-5;+\infin[$
- $f(x)=-1$ sur $\R$
- $f(x)=-7$ sur $\R$
- $f(x)=0$ sur $]-\infin;-1]$
- $f(x)=1000$ sur $\R$
Justifier que les fonctions suivantes sont continues sur $\R$
- $f(x)=\frac{x^3-4x^2+5x+7}{1+x^2}$
- $g(x)=(x^5-x^3)e^{-x}$
- $h(x)=\sqrt{3x^2+5}$
- $k(x)=e^{-x^2+3}+5e^x-1$
Justifier l'existence de solutions pour les équations suivantes dans l'intervalle précisé
- $x^3-3x+1=2$ sur $[-1;1]$
- $-x^3+4x^2-4x=1$ sur $[-5;1]$
- $3x^4+4x^3=12x^2+1$ sur $\R$
Soit $(v_n)$ la suite définie par $v_{n+1}=\sqrt{3v_n+4}$ et $v_0=0$
- Montrer par récurrence sur $n$ que $0\leq v_n \leq v_{n+1} \leq 4$
- En déduire que la suite est convergente
- Utiliser le théorème du point fixe pour déterminer la valeur de cette limite
Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire
Continuité
Fiche de synthèse
Continuité
- Les fonctions polynômes sont continues sur $\R$
- La fonction valeur absolue est continue sur $\R$
- La fonction inverse est continue sur $\R^{*}$
- La fonction racine carrée est continue sur $\R^{+}$
- La fonction exponentielle est continue sur $\R$
Contenu Complet Premium
Pour accéder au contenu complet de cette fiche de cours, vous devez vous abonner à notre offre premium.
Avec l'abonnement premium :
- Fiches de cours complètes
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Vidéos explicatives détaillées


