On considère le cercle trigonométrique ci-dessous sur lequel on a placé plusieurs points. Associer chacun des points représentés aux nombres réels

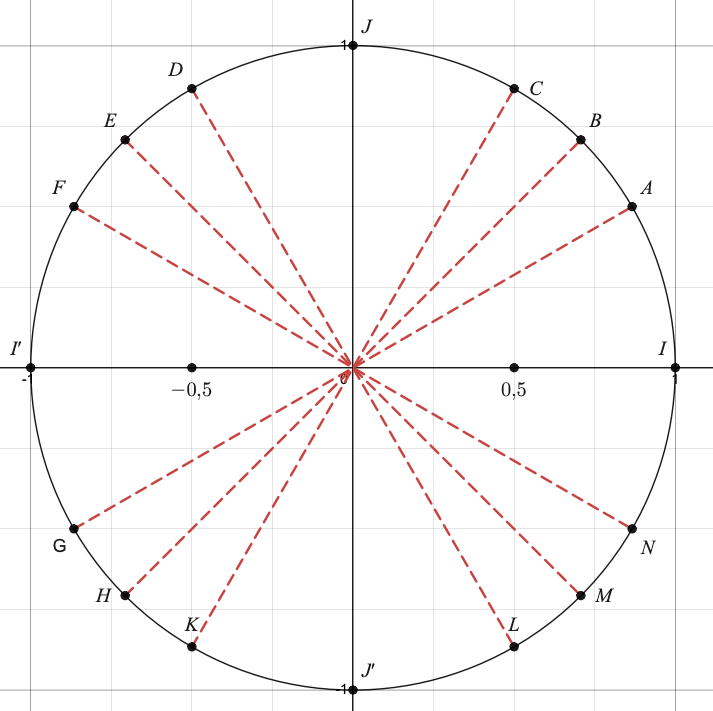
$\frac{\pi}{3}$, $\pi$, $-\frac{3\pi}{4}$, $\frac{\pi}{6}$, $\frac{3\pi}{2}$

On considère le cercle trigonométrique ci-dessous sur lequel on a représenté les 4 quadrants. Indiquer pour chacun des nombres réels suivants dans quel quadrant il se trouve.

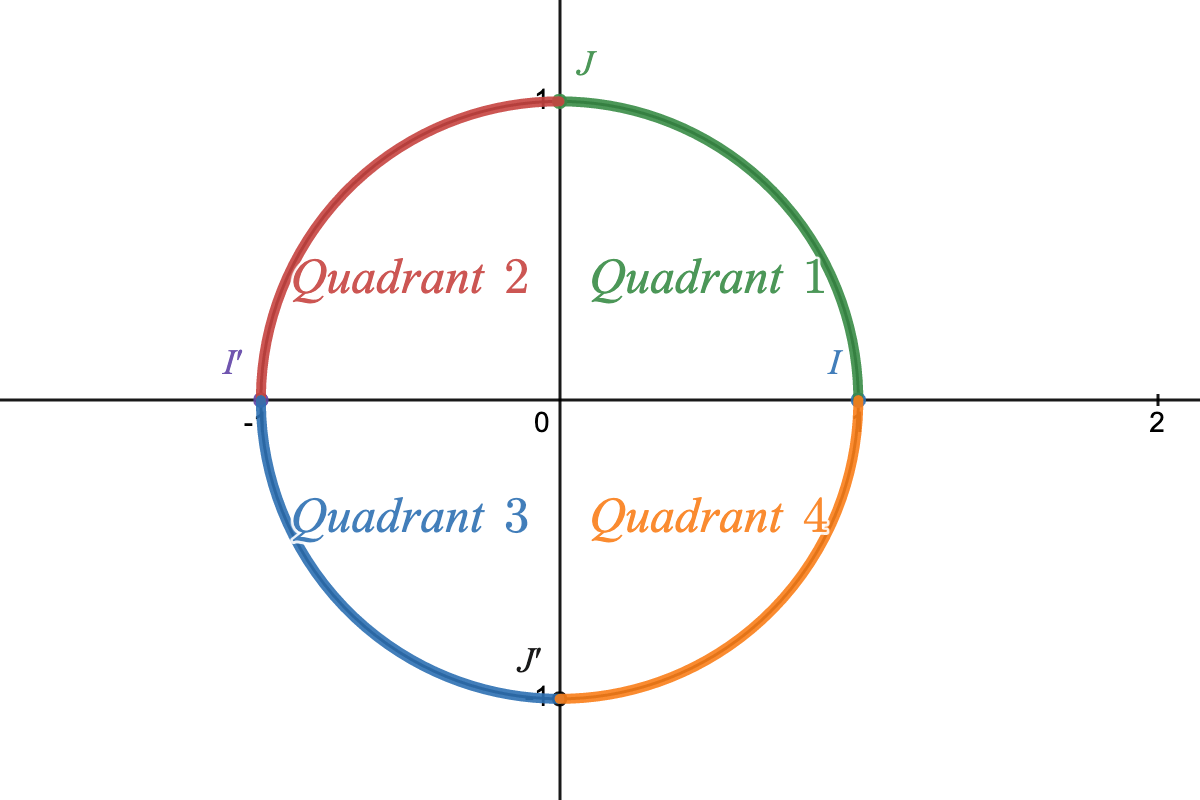
$\frac{2\pi}{3}$, $-\frac{\pi}{4}$, $\frac{3\pi}{8}$, $\frac{6\pi}{5}$, $\frac{-7\pi}{6}$

Pour chacun des couples de nombres réels, indiquer s'ils sont associés au même point image sur le cercle trigonométrique

1. $\frac{2\pi}{3}$ et $-\frac{16\pi}{3}$
2. $-\frac{5\pi}{2}$ et $\frac{9\pi}{2}$
3. $2001\pi$ et $655\pi$
4. $\frac{13\pi}{6}$ et $-\frac{2\pi}{3}$

Compléter le tableau ci-dessous puis convertir les angles suivants

1. $\frac{\pi}{5}$ en degrés
2. $270˚$ en radians
3. $\frac{4\pi}{3}$ en degrés
4. $50˚$ en radians
5. $35˚$ en radians

Sans utiliser la calculatrice donner la valeur exactes des nombres suivants

1. $cos(\frac{\pi}{3})$
2. $sin(\frac{-\pi}{4})$
3. $sin(\frac{5\pi}{6})$
4. $cos(\frac{13\pi}{3})$
5. $cos(\frac{11\pi}{2})$
6. $sin(\frac{-15\pi}{6})$

$x$ est un nombre réel. Trouver les valeurs possible de $cos(x)$ ou $sin(x)$ associé au même angle.

1. Si $cos(x)=0,6$ trouver $sin(x)$
2. Si $sin(x)=0,1$ trouver $cos(x)$
3. $x\in [0;\frac{\pi}{2}]$ et a pour cosinus $\frac{1}{3}$
   1. Trouver la valeur de son sinus
   2. Donner une valeur approchée de $x$ à $10^{-2}$ près.
   3. Reprendre la question a) pour $x\in [-\frac{\pi}{2};0]$