Afin de conserver au fil des années un parc en bon état, un loueur de vélos se sépare chaque hiver de 20% de son stock et achète ensuite 35 nouveaux vélos.
On modélise la situation par une suite $(u_n)$ où, pour tout entier naturel n, $u_n$ représente le nombre de vélos présents dans le stock de ce loueur au 1er juillet de l’année (2018 + n).
Au 1er juillet 2018, le loueur possède 150 vélos, ainsi $u_0 = 150$.

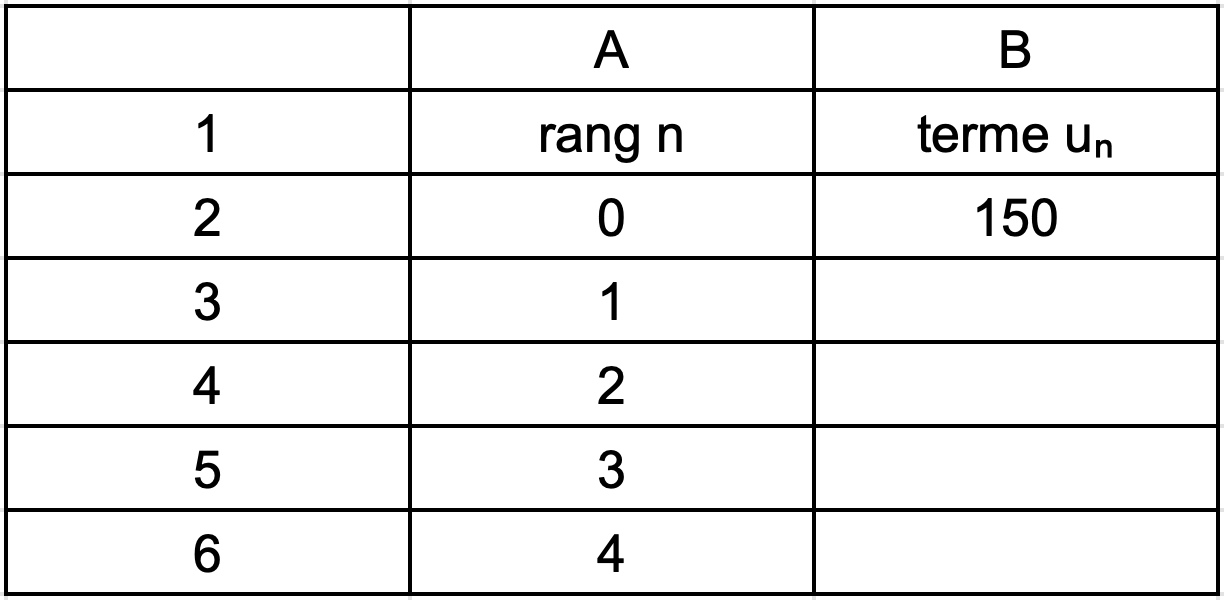
1. Déterminer la valeur de $u_0$ puis les valeurs de $u_1$ et $u_2$. En déduire la relation entre $u_{n+1}$ et $u_n$.
2. Quelle formule faut-il saisir dans la cellule B3 pour obtenir les termes successifs de la suite $(u_n)$?
   
3. Pour les termes de rang 36,37,38,39,40 on obtient les valeurs suivantes. Conjecturer la limite de la suite.
   
4. On admet que tout entier $n$, $u_n \leq 175$. Montrer que la suite est croissante.

Etudier la monotonie des suites suivantes

1. Pour tout entier naturel $n$: $u_n=7\times 2^n$
2. La suite définie par: $\begin{cases}a_{0}=-1\\ a_{n+1}=a_{n}+8-3n\end{cases}$
3. Pour tout entier naturel $n$: $v_n=\dfrac{1-n}{n+2}$
4. Pour tout entier naturel $n$: $w_n=2n^2+7n-5$

On considère l'algorithme suivant

1. Quelle est la relation entre $u_{n+1}$ et $u_n$?
2. Que calcule cet algorithme?
3. En utilisant le tableau ci-dessous déterminer la valeur renvoyée par l'algorithme.
   

Dans un repère orthonormé on a représenté la fonction $f$ définie sur $\R$ par $f(x)=\frac{1}{2}x+2$ et la droite d'équation $y=x$.
On definit la suite $(u_n)$ par $\begin{cases}u_{0}=1\\ u_{n+1}=\frac{1}{2}u_{n}+2\end{cases}$

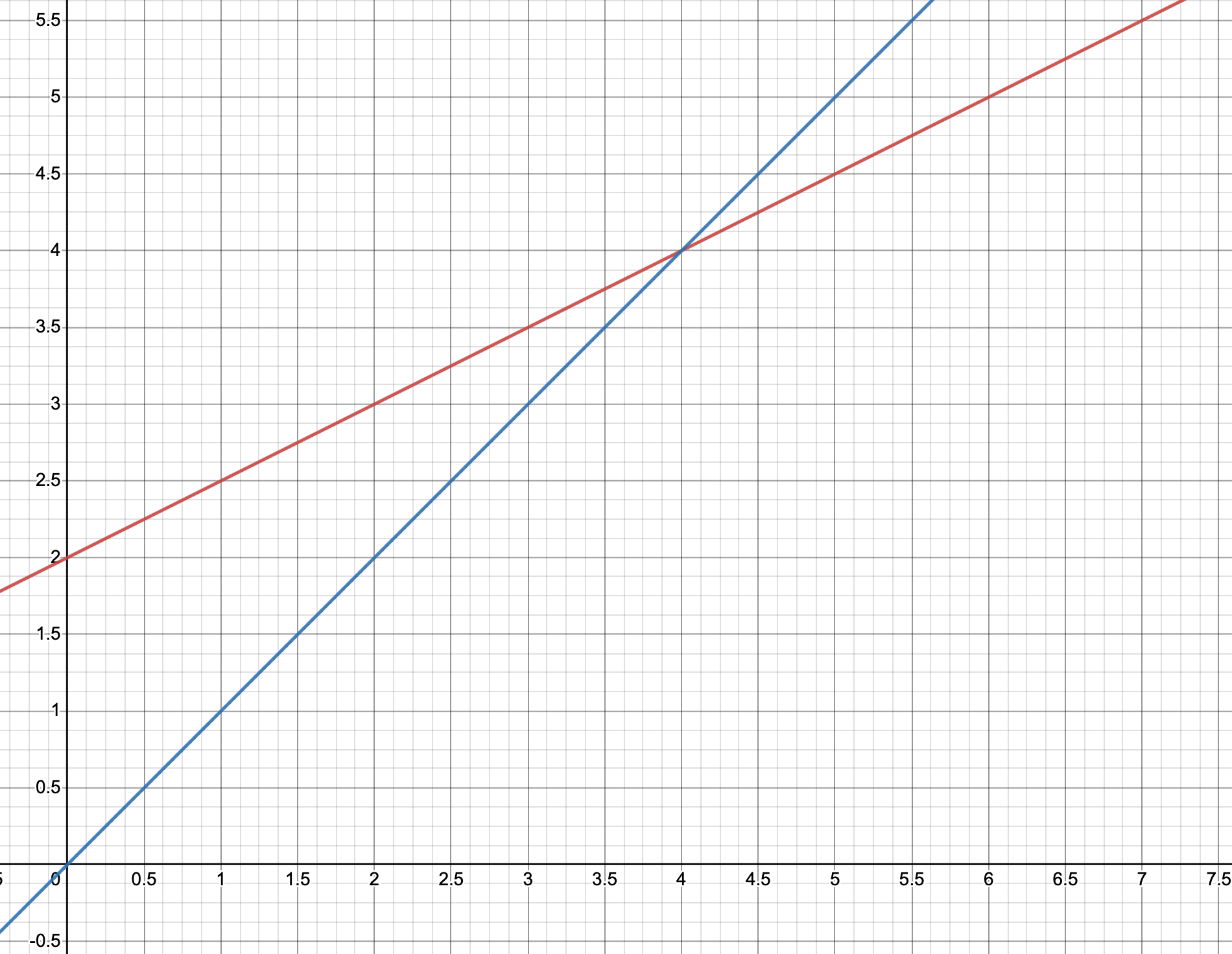
1. Représenter les 4 premiers termes de la suite sur l'axe des abscisses
2. Conjecturer le sens de variation de la suite
3. Conjecturer la limite de la suite

Chloé dépose le 1er janvier 2022, 500€ sur un compte épargne. Chaque année cette somme d'argent augmente de 1,7% et le 1ere janvier de chaque année Chloé ajoute 50€. $u_n$ représente donc la somme d'argent sur le compte épargne le 1er janvier de l'année 2022+n

1. Déterminer la valeur de $u_0$ puis les valeurs de $u_1$ et $u_2$
2. Exprimer $u_{n+1}$ en fonction de $u_n$
3. En admettant que la suite est positive, démontrer qu'elle est croissante.
4. À l'aide de la calculatrice déterminer l'année à partir de la quelle Chloé doublera sa somme initiale.

Etudier la monotonie des suites suivantes

1. Pour tout entier naturel $n$: $u_n=\dfrac{5^n}{n}$
2. Pour tout entier naturel $n$: $v_n=1-2n^2$
3. La suite définie par: $\begin{cases}w_{0}=-5\\ w_{n+1}=w_{n}-w_{n}^2-3\end{cases}$
4. Pour tout entier naturel $n$: $t_n=\dfrac{1}{n}-\dfrac{1}{n+1}$

On considère la suite définie pour tout entier naturel par $u_n=\dfrac{1}{2n+7}$

1. Justifier que pour tout entier naturel $n$, $2n+7>0$
2. Demontrer que pour tout entier naturel $n$, $\dfrac{u_{n+1}}{u_n}=\dfrac{2n+7}{2n+9}$
3. Jutifier que $2n+7<2n+9$ et en déduire que $\dfrac{2n+7}{2n+9}<1$
4. Conclure

Pour chacune des suites suivantes exprimer $u_{n-1}$ et $u_{2n+1}$ en fonction de $n$

1. $u_n=5-7n$
2. $v_n=3n^2-4$
3. $w_n=\dfrac{2-3n}{1+n^2}$

Dans un repère orthonormé on a représenté la fonction $f$ définie sur $\R$ par $f(x)=\dfrac{6}{1+x}$.
On definit la suite $(u_n)$ par $\begin{cases}u_{0}=1\\ u_{n+1}=\frac{6}{1+u_n}\end{cases}$

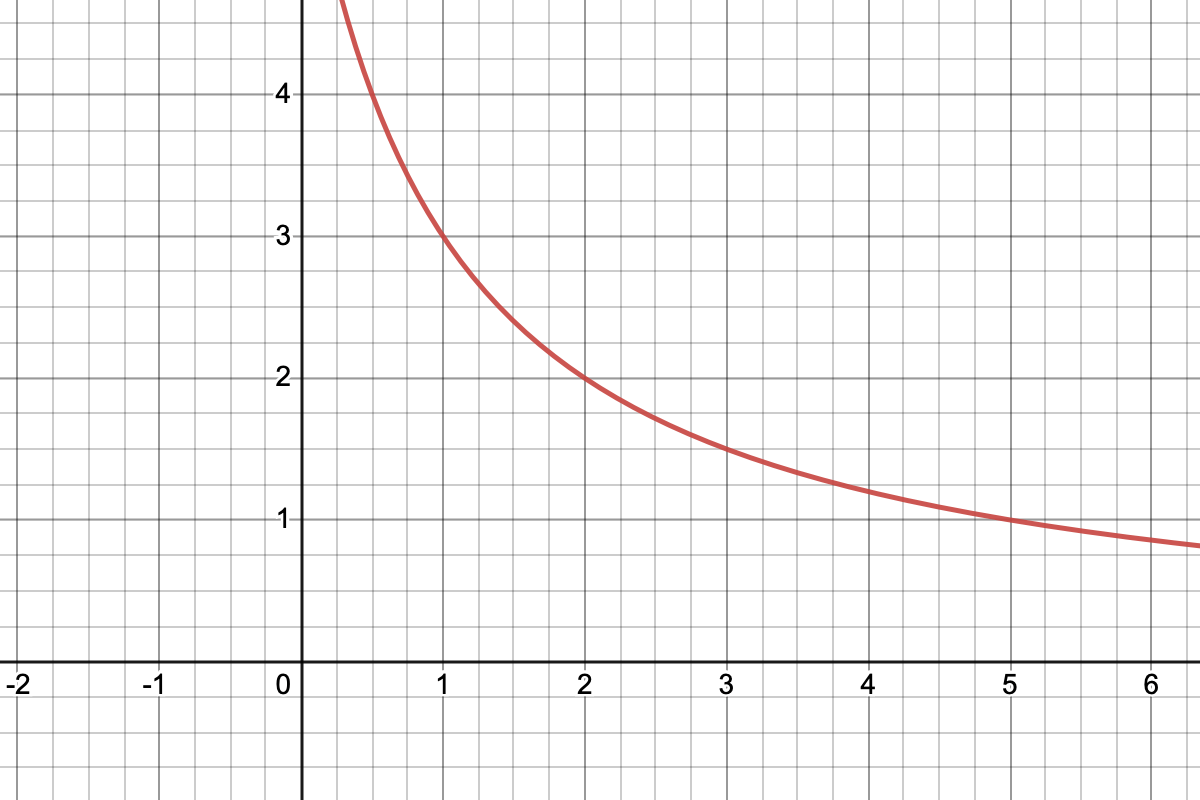
1. Représenter les 4 premiers termes de la suite sur l'axe des abscisses
2. Conjecturer le sens de variation de la suite
3. Conjecturer la limite de la suite