
Les exercices
0%
Exercice 1 - Calculer les termes d'une suite explicite
Calculer les 3 premiers termes des suites suivantes
Gratuit
Exercice 2 - Calculer les termes d'une suite définie par récurrence
Calculer les 3 premiers termes des suites suivantes
- et
- et
- et
Exercice 3 - Représenter graphiquement les termes d'une suite
Représenter graphiquement les 4 premiers termes des suites suivantes
- et
- et
Exercice 4 - Exprimer différents indice en fonction de n
Pour chacune des suites suivantes exprimer et en fonction de
Exercice 5 - Trouver la relation entre 2 termes consécutifs
Donner la relation entre et sachant qu'à chaque étape
- double
- diminue de 6,5
- diminue de 8%
- triple et augmente de 7
- augmente de 12% et baisse de 50
Gratuit
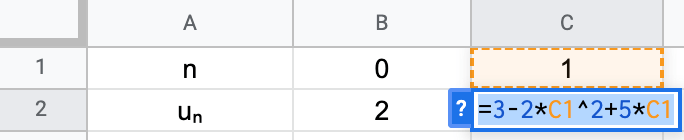
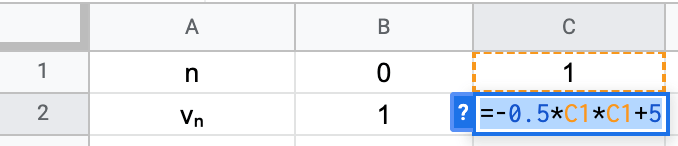

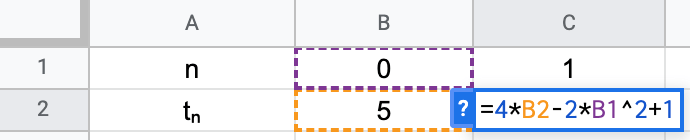
Exercice 6 - Définir une suite avec un tableur
Utiliser le tableur pour exprimer les suites sous forme explicite ou par récurrence




Exercice 7 - Définir une suite avec un algorithme
Pour les suites suivantes, indiquer la dernière valeur calculée lorsque la suite a une formule explicite et exprimer en fonction de ou en fonction de
Pour i allant de 1 à 8
U ← 3i+2
Fin Pour U ← 3
Pour k allant de 1 à 4
U ← (U-2)/(U+5)
Fin Pour j=0
while j < 12
u = j(j-1)+3
j = j+1 u = 4
for i in range(1,8)
u = u**2+2*u+1
print(u)


