Utiliser les formes canoniques suivantes pour faire le tableau de variations de chaque polynôme.

1. $2(x-1)^2+5$
2. $-(x+3)^2+1$
3. $(x-4)^2-10$
4. $(x+3)^2$

Déterminer le nombre de racines de chaque polynôme grâce au discriminant.

1. $x^2-5x-6$
2. $-3x^2+2x-1$
3. $x^2+2\sqrt{2}x+2$
4. $-x^2-x+20$

Résoudre dans $\R$ chaque équation grâce au discriminant.

1. $2x^2-4x-6$
2. $-x^2-x+20$
3. $-x^2-8x+16$
4. $x^2-x-11$

Ecrire les polynômes suivants sous forme factorisée lorsque c'est possible.

1. $x^2-3x-4$
2. $2x^2+x+\frac{1}{2}$
3. $3x^2-24x+16$
4. $x^2+\sqrt{2}x-1$

Résoudre dans $\R$ chaque inéquation.

1. $2x^2-4x-6>0$
2. $-x^2+9x-20\geq 0$
3. $3x^2+x+1<0$
4. $x^2+10x+25\leq 0$

La figure ci-dessous représente un terrain rectangulaire dans lequel on veut créer un chemin (en vert). La largeur $x$ de ce chemin doit être supérieure à 0,8m et on souhaite que la partie restante ait une aire supérieure à $280m^2$

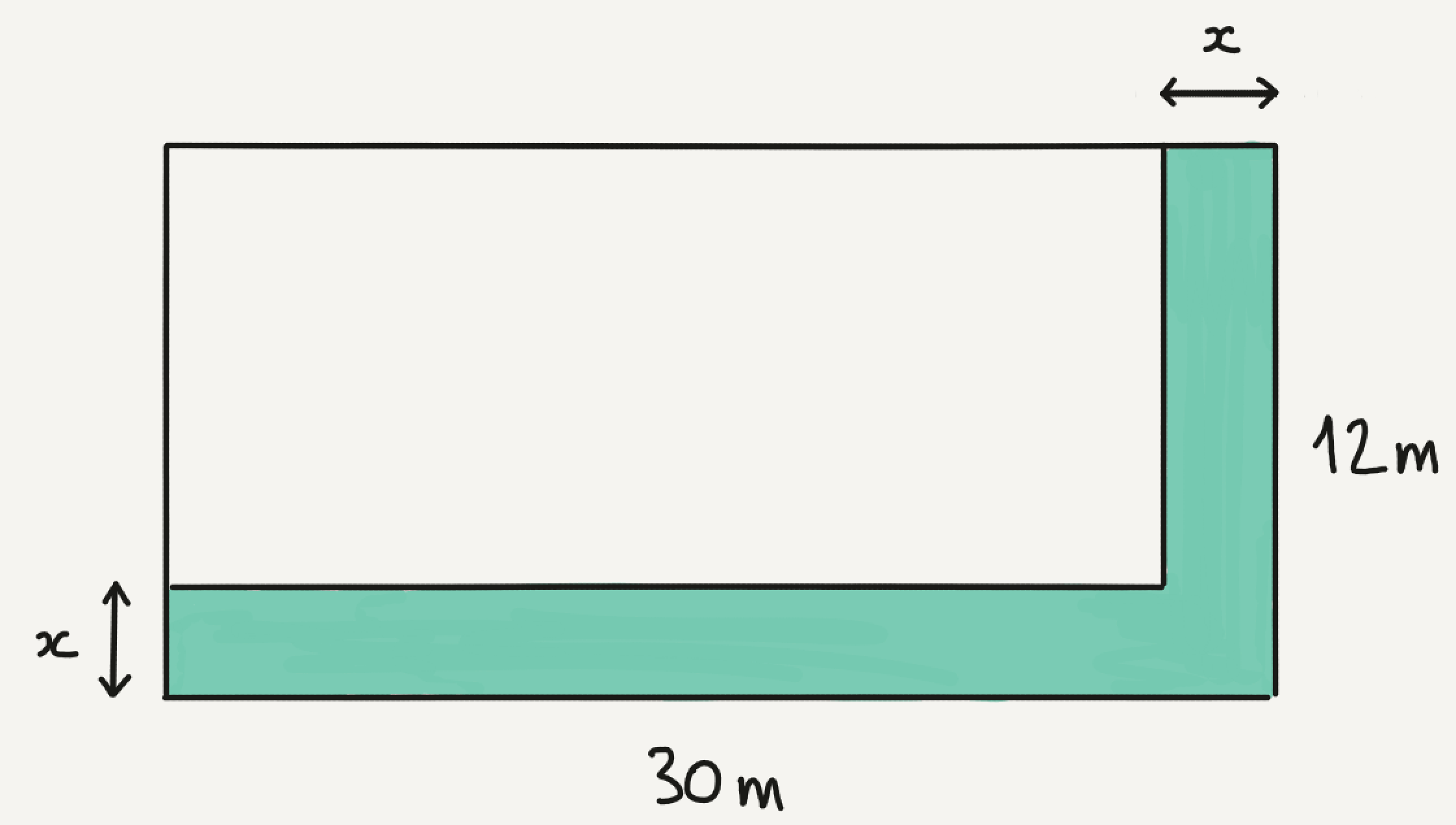
1. À quel intervalle appartient la largeur $x$ du chemin?
2. Montrer que $x$ vérifie l'inéquation $x^2-42x+80\geq 0$
3. En déduire les valeurs possibles de $x$