Dans la figure ci-dessous, les vecteurs $\vec{F_1}$ et $\vec{F_2}$ représentent deux forces de valeurs respectives $12~N$ et $10~N$.

1. L'unité de valeur de ces forces est le Newton ($N$)
2. Le quadrilatère formé par les forces $\vec{F_1}$ et $\vec{F_2}$ et les pointillés est un parallélogramme
3. L'angle formé par les vecteurs $\vec{F_1}$ et $\vec{F_2}$ vaut 56˚
4. Le vecteur $\vec{F}$ nommé la résultante des forces est tel que $\vec{F}=\vec{F_1}+\vec{F_2}$

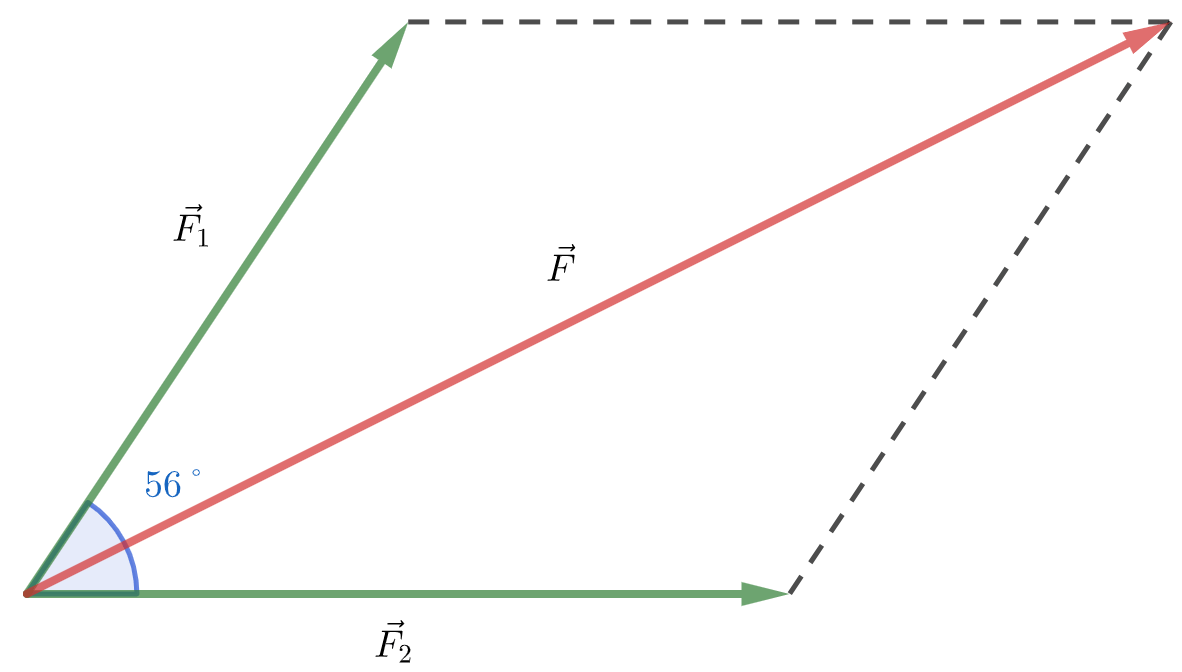
À l'aide du produit scalaire, déterminer la valeur de la résultante des forces $\vec{F}$.

On considère le rectangle $ABCD$ de longueur 14 et de largeur 8.

1. $E$ est le milieu de $[BC]$
2. $F$ est le milieu de $[CD]$

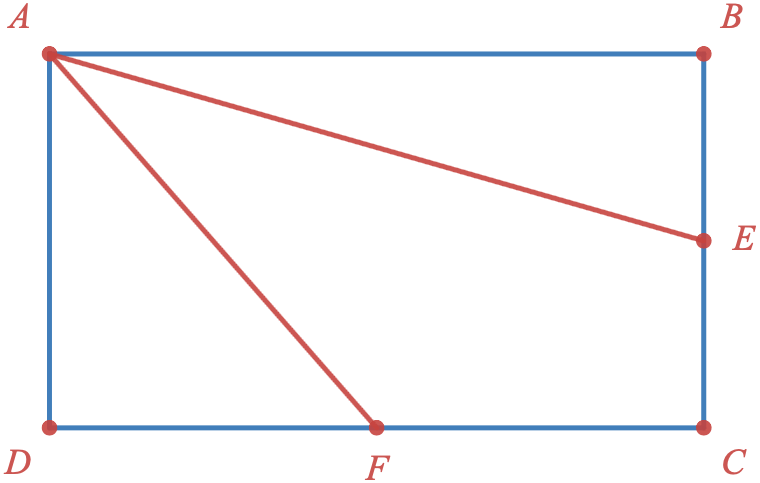
Calculer les produits scalaires suivants.

1. $\overrightarrow{AB}.\overrightarrow{AF}$
2. $\overrightarrow{DC}.\overrightarrow{CB}$
3. $\overrightarrow{BA}.\overrightarrow{DF}$
4. $\overrightarrow{AE}.\overrightarrow{AF}$
5. $\overrightarrow{FA}.\overrightarrow{FD}$
6. $\overrightarrow{AE}.\overrightarrow{AC}$

On considère le triangle rectangle isocèle $ABC$

1. $AC=BC=EC=1$
2. $AED$ est rectangle en $D$

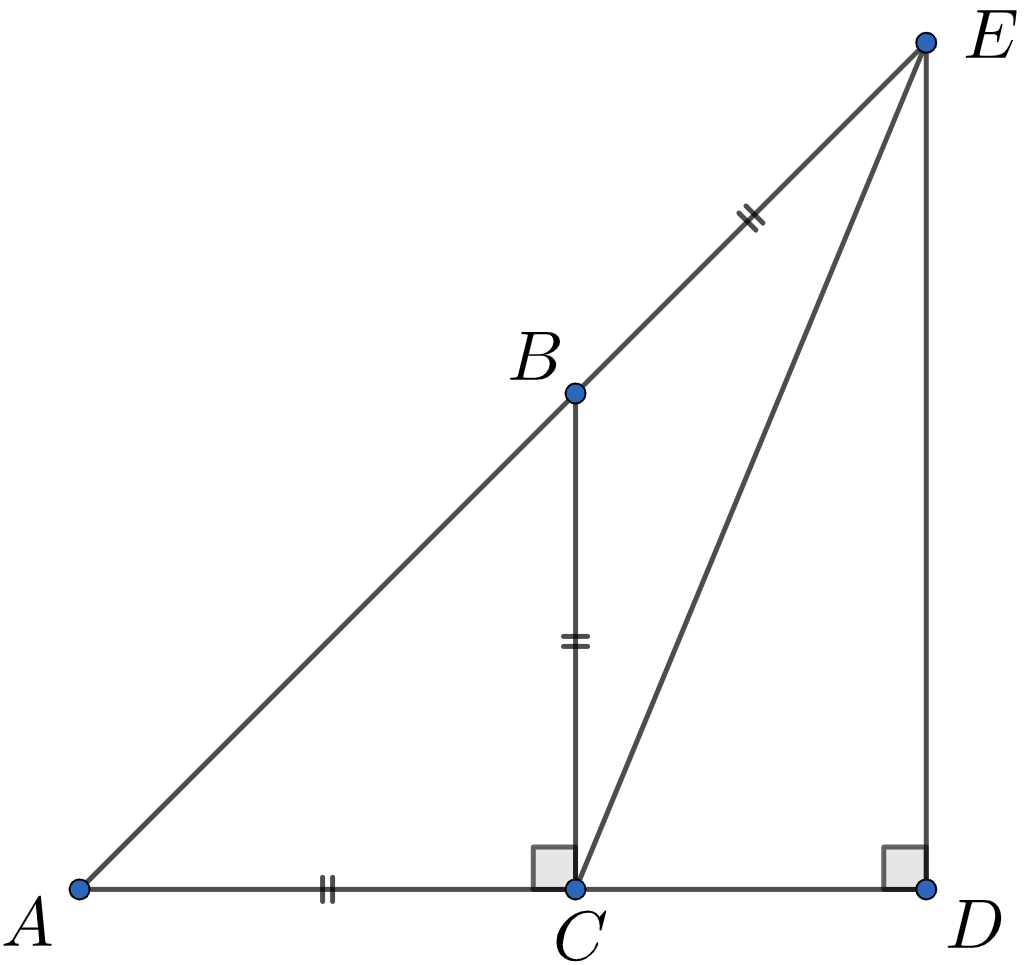
Calculer les produits scalaires suivants.

1. Montrer que $AE=1+\sqrt{2}$.
2. Calculer le produit scalaire $\overrightarrow{AC}.\overrightarrow{AE}$.
3. En utilisant le fait $\overrightarrow{AC}.\overrightarrow{AE}=AC^2+AE^2-EC^2$, montrer que $EC=\sqrt{2+\sqrt{2}}$.
4. Montrer que $\widehat{AEC}=\frac{\pi}{8}$.
5. Calculer de deux façons différentes le produit scalaire $\overrightarrow{EA}.\overrightarrow{EC}$
6. En déduire que $cos(\frac{\pi}{8})=\frac{\sqrt{2+\sqrt{2}}}{2}$ puis déterminer la valeur de $sin(\frac{\pi}{8})$.