On considère les points $A(4;1)$, $B(0;5)$ et $C(-2;-1)$

1. Calculer $\overrightarrow{AB}.\overrightarrow{AC}$
2. En déduire que $cos(\widehat{BAC})=\frac{1}{\sqrt{5}}$
3. Calculer la mesure de l'angle $\widehat{BAC}$ au degré près

Dans le repère orthonormé $(O;\vec{i};\vec{j})$ on considère les vecteurs $\vec{u}=-2\vec{i}$ et $\vec{v}=-\frac{1}{2} \vec{i}+\frac{\sqrt{3}}{2}\vec{j}$

1. Calculer $(\vec{u}+\vec{v}).(\vec{u}-\vec{v})$
2. Calculer $||\vec{u}+\vec{v}||^2-||\vec{u}-\vec{v}||^2$
3. Montrer que les vecteurs $(\vec{u}+2\vec{v})$ et $(\vec{u}-2\vec{v})$ sont orthogonaux

On considère les vecteurs $\vec{u}$ et $\vec{v}$

1. Exprimer $\vec{u}.\vec{v}$ en fonction de $||\vec{u}||$, $||\vec{v}||$ et $||\vec{u}-\vec{v}||$
2. En déduire que pour tous les points $A$, $B$ et $C$ du plan on a: $\overrightarrow{AB}.\overrightarrow{AC}=\frac{1}{2}(AB^2+AC^2-CB^2)$
3. Soit un triangle $ABC$ tel que $AB=2$, $AC=4$ et $BC=5$. Calculer les produits scalaires:
   
   1. $\overrightarrow{AB}.\overrightarrow{AC}$
   2. $\overrightarrow{BA}.\overrightarrow{BC}$
   3. $\overrightarrow{CA}.\overrightarrow{CB}$

Déterminer les valeurs éventuelles du réel $t$ pour lesquelles les vecteurs $\vec{u}$ et $\vec{v}$ sont orthogonaux

1. $\vec{u}\dbinom{5t-3}{-1}$ et $\vec{v}\dbinom{-2}{t+2}$
2. $\vec{u}\dbinom{-8}{-2t}$ et $\vec{v}\dbinom{-2}{t}$
3. $\vec{u}\dbinom{t+2}{\frac{1}{4}-t}$ et $\vec{v}\dbinom{t}{4}$

$ABCD$ est un carré de coté 1 et le point $E$ est tel que $BCE$ est un triangle équilatéral.

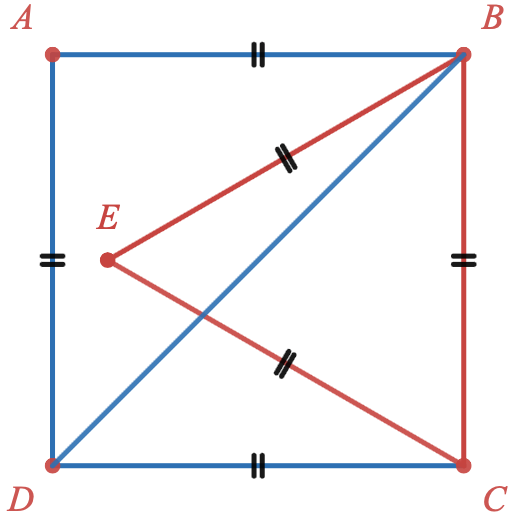
1. Montrer que $\widehat{DBE}=\frac{\pi}{12}$
2. Soit $F$ le projeté orthogonal de $E$ sur $(BC)$. Montrer que $EF=\frac{\sqrt{3}}{2}$.

On se place dans le repère $(D; \overrightarrow{DC}; \overrightarrow{DA})$

3. Déterminer les coordonnées du point $E$.
4. Calculer $\overrightarrow{BE}.\overrightarrow{BD}$
5. En déduire que $cos(\frac{\pi}{12})=\frac{\sqrt{2}+\sqrt{6}}{4}$