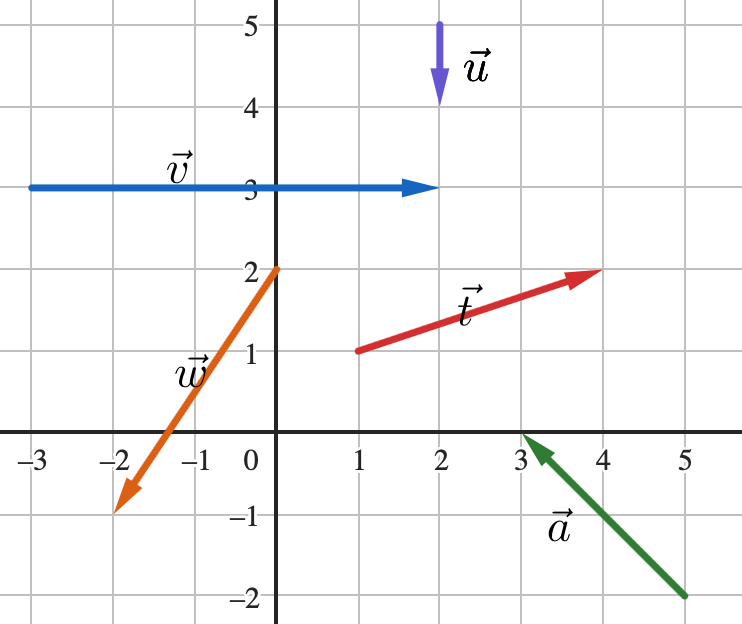
Déterminer les coordonnées des vecteurs ci-dessous puis calculer leurs normes.

Calculer le produit scalaire $\overrightarrow{AB}.\overrightarrow{AC}$ en utilisant la formule la plus adaptée.

1. $\overrightarrow{AB}\binom{3}{-2}$ et $\overrightarrow{AC}\binom{-5}{-10}$
2. $AB=4$, $AC=3\sqrt{2}$ et $(\overrightarrow{AB}, \overrightarrow{AC})=-\frac{\pi}{4}$
3. $A(-1;5)$, $B(4;7)$ et $C(3;0)$
4. $AB=5$ et $AH=2$ avec $H$ le pied de la hauteur issue de $C$ avec $H\in [AB)$
5. $A$, $B$ et $C$ sont alignés avec $AB=4,5$, $AC=8$ et $B\in [AC]$

On considère le rectangle ci-dessous. Utiliser la formule du projeté orthogonal pour déterminer les produits scalaires suivants

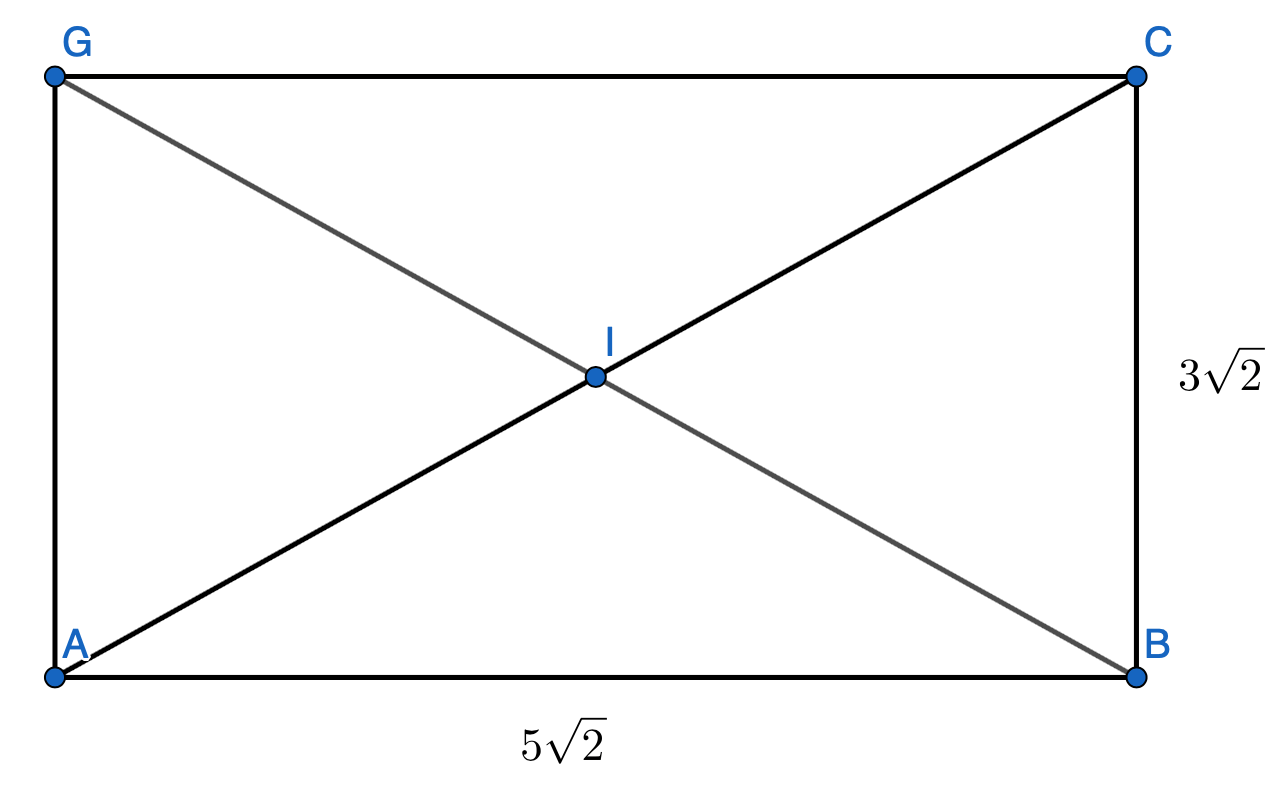
1. $\overrightarrow{BG}.\overrightarrow{BA}$
2. $\overrightarrow{AI}.\overrightarrow{AB}$
3. $\overrightarrow{GA}.\overrightarrow{GI}$
4. $\overrightarrow{CA}.\overrightarrow{CB}$

On considère le triangle ci-dessous. Déterminer les produits scalaires suivants

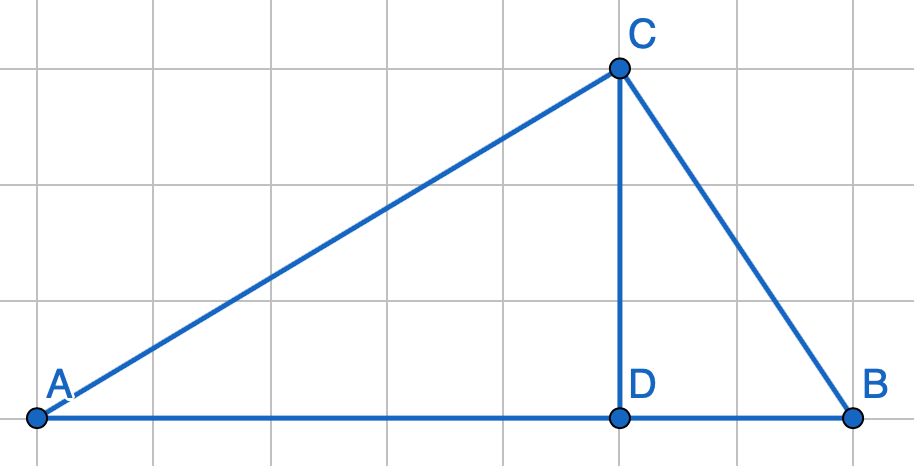
1. $\overrightarrow{CD}.\overrightarrow{CB}$
2. $\overrightarrow{AC}.\overrightarrow{AB}$
3. $\overrightarrow{BA}.\overrightarrow{BC}$
4. $\overrightarrow{DB}.\overrightarrow{DA}$

On considère les vecteurs $\vec{u}\dbinom{-5}{4}$ et $\vec{v}\dbinom{2}{\frac{3}{2}}$. Calculer les produits scalaires suivants

1. $\vec{u}.\vec{v}$
2. $-\vec{u}.(\vec{u}-\vec{v})$
3. $(2\vec{u}-\vec{v}).(\vec{u}+4\vec{v})$
4. $(\vec{u}-\vec{v})^2$

Dans un repère orthonormé, on considère les points suivants: $A(-10;4)$, $B(-4;1)$ et $C(-1;7)$

1. En utilisant le produit scalaire, montrer que le triangle ABC est rectangle et préciser l'angle droit
2. En déduire $\overrightarrow{BA}.\overrightarrow{BC}$
3. Déterminer les coordonnées du point $D$ pour que $ABCD$ soit un rectangle