On considère le carré $ABCD$ ci-dessous.
Les points $E$ et $F$ sont définis tels que $\overrightarrow{BE}=\frac{1}{4}\overrightarrow{BA}$ et $\overrightarrow{CF}=\frac{1}{4}\overrightarrow{CB}$

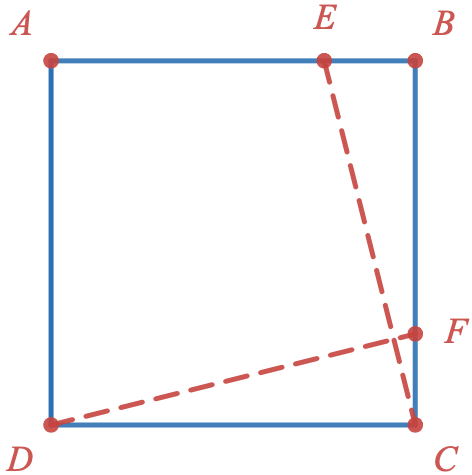
En utilisant la relation de Chasles, montrer que les droites $(DF)$ et $(CE)$ sont perpendiculaires.

$ABC$ est un triangle quelconque, $A'$, $B'$ et $C'$ sont les milieux respectifs des côtés $[BC]$, $[AC]$ et $[AB]$.
Le point $G$ est défini par la relation $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$

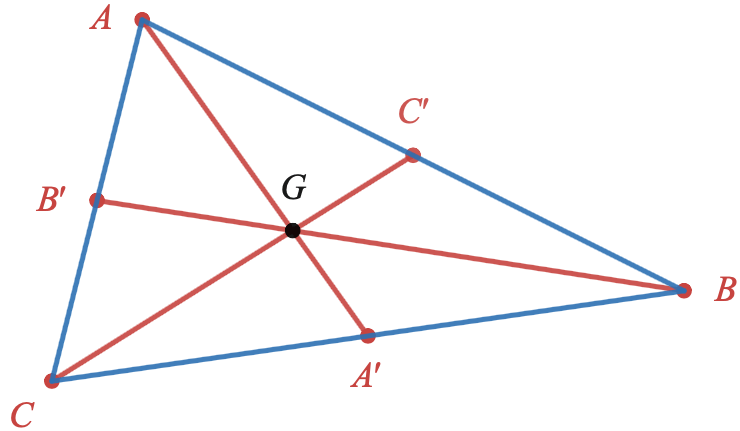
1. Montrer que $\overrightarrow{AG}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC})$
2. En déduire que $\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AA'}$
3. De même, montrer que $\overrightarrow{BG}=\frac{2}{3}\overrightarrow{BB'}$ et $\overrightarrow{CG}=\frac{2}{3}\overrightarrow{CC'}$
4. En déduire que le point $G$ est le point d'intersection des médianes du triangles.

Soit $M$ un point du plan. Déterminons le point $M$ qui rend la quantité $MA^2+MB^2+MC^2$ minimale.

5. Prouver que $MA^2+MB^2+MC^2=(\overrightarrow{MG}+\overrightarrow{GA})^2+(\overrightarrow{MG}+\overrightarrow{GB})^2+(\overrightarrow{MG}+\overrightarrow{GC})^2$.
6. En déduire que $MA^2+MB^2+MC^2=3\overrightarrow{MG}^2+\overrightarrow{GA}^2+\overrightarrow{GB}^2+\overrightarrow{GC}^2$.
7. En déduire le point $M$ qui minimise la quantité $MA^2+MB^2+MC^2$.

On considère le parallelogramme $ABCD$ ci-dessous.

1. Montrer que $AB^2-AD^2=\overrightarrow{AC}.\overrightarrow{DB}$
2. Que peut-on en déduire pour les diagonales d'un losange et d'un carré?
3. Montrer que $\overrightarrow{AB}.\overrightarrow{BC}=\frac{1}{2}(AC^2-AB^2-AD^2)$
4. Si $ABCD$ est un rectangle, quelle identité retrouve-t'on?

On considère le triangle $ABC$ rectangle en $C$ ci-dessous.

1. $I$ est le projeté orthogonal de $C$ sur $(AB)$
2. $K$ est le projeté orthogonal de $I$ sur $(AC)$
3. $J$ est le projeté orthogonal de $I$ sur $(CB)$
4. $L$ est le milieu de $[CB]$

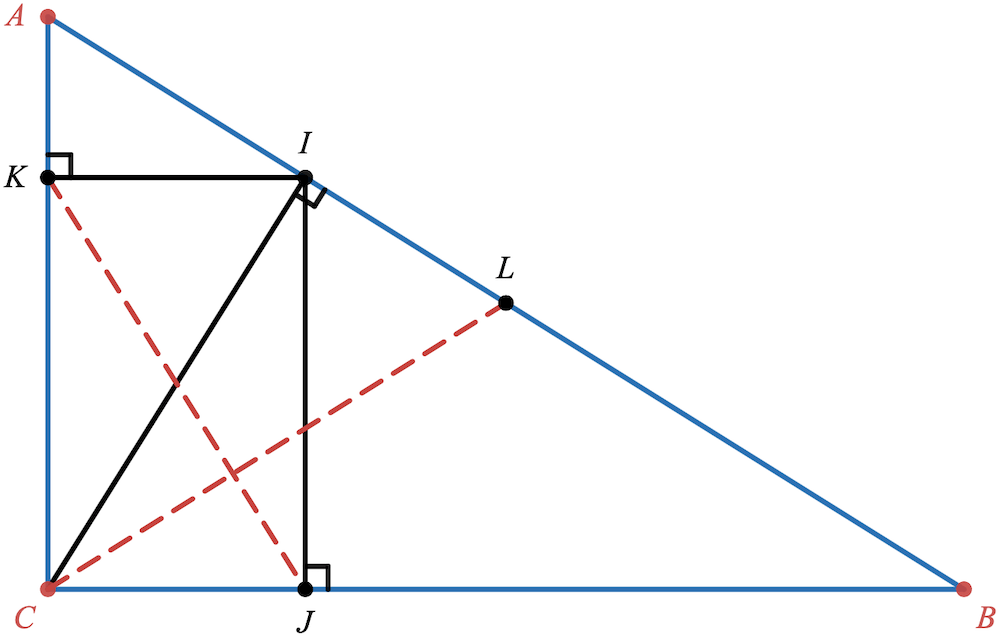
1. Montrer que $\overrightarrow{CA}.\overrightarrow{KJ}=\overrightarrow{CA}.\overrightarrow{IC}$ et $\overrightarrow{CB}.\overrightarrow{KJ}=\overrightarrow{CB}.\overrightarrow{CI}$
2. En utilisant la relation de Chasles, montrer que $\overrightarrow{CA}.\overrightarrow{KJ}+\overrightarrow{CB}.\overrightarrow{KJ}=2\overrightarrow{CL}.\overrightarrow{KJ}$
3. En deduire que $\overrightarrow{CL}.\overrightarrow{KJ}=0$ et conclure.

On considère le cercle de centre $O$ et rayon 1. $A$ et $B$ sont deux points du cercle.

1. On se place dans le repère orthonormé $(O;\vec{i};\vec{j})$
2. $\alpha$ est la mesure de l'angle $\widehat{AOI}$
3. $\beta$ est la mesure de l'angle $\widehat{BOI}$

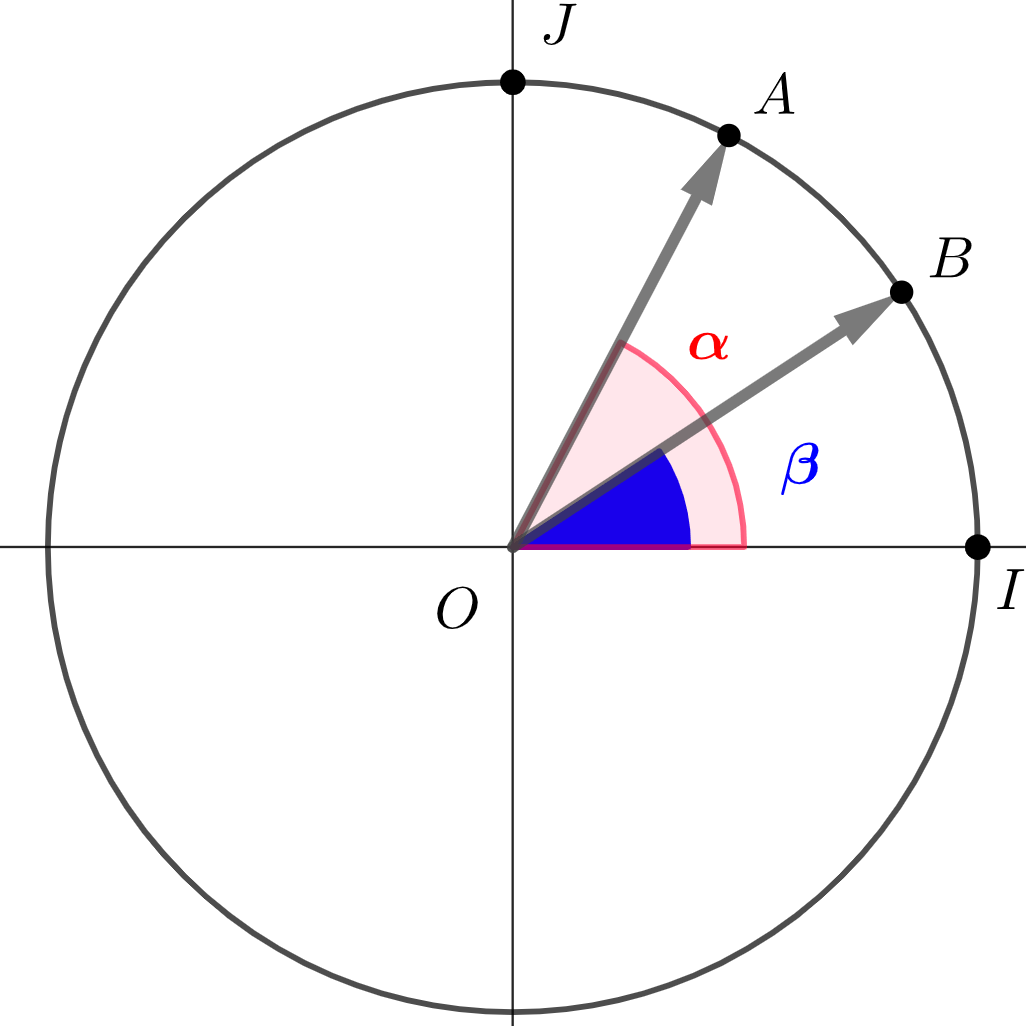
1. Montrer que $\overrightarrow{OA}=cos(\alpha)\vec{i}+sin(\alpha)\vec{j}$ et $\overrightarrow{OB}=cos(\beta)\vec{i}+sin(\beta)\vec{j}$
2. Utiliser le résultat précédent pour calculer $\overrightarrow{OA}.\overrightarrow{OB}$.
3. Déterminer $\overrightarrow{OA}.\overrightarrow{OB}$ en fonction de $\alpha$ et $\beta$ en utilisant une formule du cours.
4. En déduire une expression de $cos(\alpha-\beta)$ puis de $cos(\alpha+\beta)$.
5. Utiliser les valeurs de $cos$ et $sin$ de $\frac{\pi}{6}$ et $\frac{\pi}{4}$ pour déterminer les valeurs exactes de $cos(\frac{\pi}{12})$ et $sin(\frac{\pi}{12})$.