Lors d'une soirée, une chaîne de télévision a retransmis un match. Cette chaîne a ensuite proposé une émission d'analyse de ce match. On dispose des informations suivantes:

1. 56 % des téléspectateurs ont regardé le match;
2. un quart des téléspectateurs ayant regardé le match ont aussi regardé l'émission ;
3. 16,2 % des téléspectateurs ont regardé l'émission.

On interroge au hasard un téléspectateur. On note les évènements :

1. $M$ : « le téléspectateur a regardé le match » ;
2. $E$ : « le téléspectateur a regardé l'émission ».

On note $x$ la probabilité qu'un téléspectateur ait regardé l'émission sachant qu'il n'a pas regardé le match.

1. Construire un arbre pondéré illustrant la situation.
2. Déterminer la probabilité de $M\cap E$.
3. Vérifier que $P(E)=0,44x+0,14$.
4. En déduire la valeur de $x$.
5. Le téléspectateur interrogé n'a pas regardé l'émission. Quelle est la probabilité, arrondie à $10^{-2}$ , qu'il ait regardé le match?

Pondichery 2011

Un jeu consiste à lancer des fléchettes sur une cible. La cible est partagée en quatre secteurs, comme indiqué sur la figure ci-dessous. On suppose que les lancers sont indépendants et que le joueur touche la cible à tous les coups.

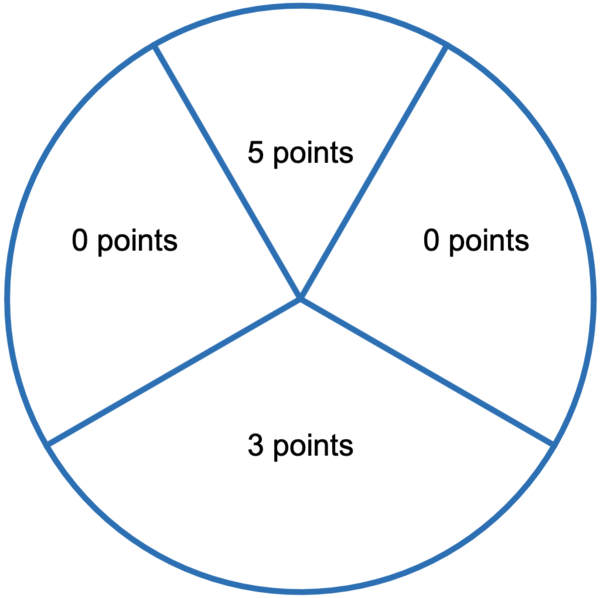
1. Le joueur lance une fléchette.
   1. On note $p_{0}$ la probabilité d'obtenir 0 point.
   2. On note $p_{3}$ la probabilité d'obtenir 3 points.
   3. On note $p_{5}$ la probabilité d'obtenir 5 points.

   On a donc $p_{0} + p_{3} + p_{5} = 1$.

   Sachant que $p_{5} = \dfrac{1}{2}p_{3}$ et que $p_{5} = \dfrac{1}{3}p_{0}$ déterminer les valeurs de $p_{0},, p_{3}$ et $p_{5}$

2. Une partie de ce jeu consiste à lancer trois fléchettes au maximum. Le joueur gagne la partie s'il obtient un total (pour les 3 lancers) supérieur ou égal à 8 points. Si au bout de 2 lancers, il a un total supérieur ou égal à 8 points, il ne lance pas la troisiéme fléchette.
   1. On note $G_{2}$ l'événement : "le joueur gagne la partie en 2 lancers".
   2. On note $G_{3}$ l'événement: "le joueur gagne la partie en 3 lancers".
   3. On note $P$ l'événement: "le joueur perd la partie".
   4. On note $p(A)$ la probabilité d'un événement $A$.
   Montrer, en utilisant un arbre pondéré, que $p(G_{2}) = \dfrac{5}{36}$.
   On admettra dans la suite que $p(G_{3}) = \dfrac{7}{36}$
3. En déduire $p(P)$
4. Un joueur joue six parties avec les règles données à la question 2. Quelle est la probabilité qu'il ne gagne aucune partie ?
5. Quelle est la probabilité qu'il gagne au moins une partie?
6. Pour une partie, la mise est fixée à 2€.
   1. Si le joueur gagne en deux lancers, il reçoit 5 €.
   2. S'il gagne en trois lancers, il reçoit 3 €.
   3. S'il perd, il ne reçoit rien.
   On note $X$ la variable aléatoire correspondant au gain algébrique du joueur pour une partie. Les valeurs possibles pour $X$ sont donc: $-2$, 1 et 3.
7. Donner la loi de probabilité de $X$.
8. Déterminer l'espérance mathématique de $X$. Le jeu est-il favorable au joueur ?