Dans une classe de 32 élèves, 18 font du basket, 24 font du foot et 6 ne font ni du foot ni du basket.

1. Recopier et compléter le tableau

	$B$	$\overline{B}$	$Total$
F
$\overline{F}$
Total

On interroge désormais un élève au hasard

2. Quelle est la probabilité que l'élève fasse du foot et du basket
3. Calculer P(B) et P(F)
4. Calculer $P_{F}(B)$

On considère une urne qui contient 5 boules bleues et 5 boules vertes. On tire successivement 2 boules de l'urne sans les remettre (on parle de tirages sans remise). On note $B$ et $V$ respectivement les événements, "la boule tirée est bleue" et "la boule tirée est verte".

1. Quelle est la probabilité d'obtenir une boule verte au premier tirage?
2. On considère que la première boule tirée est bleue, quelle est la probabilité d'obtenir une boule verte au second tirage?
3. Représenter la situation par un arbre pondéré.

Utiliser les formules de probabilités pour déterminer les probabilités inconnues

1. $P(A)=0,8$ et $P_{A}(B)=0,6$. Trouver $P(A\cap B)$
2. $P(A)=0,3$, $P(B)=0,7$ et $P(A\cup B)=0,9$. Trouver $P(A\cap B)$, $P_{A}(B)$, $P_{B}(A)$
3. Soit B un événement tel que $P(B)\not =0$, montrer que $P_{B}(A)+P_{B}(\overline{A})=1$

On considère 2 événements $R$ et $C$ et l'arbre pondéré ci-dessous.

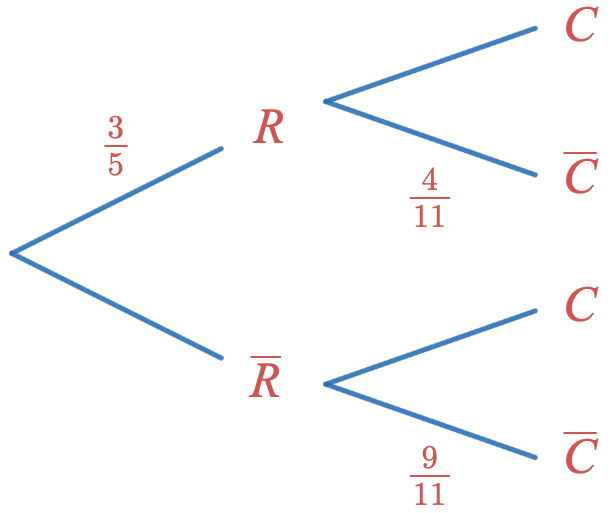
1. Compléter l'arbre pondéré ci-dessus
2. En déduire les probabilités $P(R\cap C)$, $P(R\cap \overline{C})$, $P(\overline{R}\cap C)$ and $P(\overline{R}\cap \overline{C})$
3. Déterminer la valeur de $P(C)$ et $P_C(R)$

Utiliser les formules de probabilités pour déterminer les probabilités inconnues

1. $P(A)=0,8$ et $P_{A}(B)=0,6$. Trouver $P(A\cap B)$
2. $P(A)=0,3$, $P(B)=0,7$ et $P(A\cup B)=0,9$. Trouver $P(A\cap B)$, $P_{A}(B)$, $P_{B}(A)$
3. Soit B un événement tel que $P(B)\not =0$, montrer que $P_{B}(A)+P_{B}(\overline{A})=1$

Utiliser les formules de probabilités pour déterminer les probabilités inconnues

1. $P(A)=0,8$ et $P_{A}(B)=0,6$. Trouver $P(A\cap B)$
2. $P(A)=0,3$, $P(B)=0,7$ et $P(A\cup B)=0,9$. Trouver $P(A\cap B)$, $P_{A}(B)$, $P_{B}(A)$
3. Soit B un événement tel que $P(B)\not =0$, montrer que $P_{B}(A)+P_{B}(\overline{A})=1$

Utiliser les formules de probabilités pour déterminer les probabilités inconnues

1. $P(A)=0,8$ et $P_{A}(B)=0,6$. Trouver $P(A\cap B)$
2. $P(A)=0,3$, $P(B)=0,7$ et $P(A\cup B)=0,9$. Trouver $P(A\cap B)$, $P_{A}(B)$, $P_{B}(A)$
3. Soit B un événement tel que $P(B)\not =0$, montrer que $P_{B}(A)+P_{B}(\overline{A})=1$

Utiliser les formules de probabilités pour déterminer les probabilités inconnues

1. $P(A)=0,8$ et $P_{A}(B)=0,6$. Trouver $P(A\cap B)$
2. $P(A)=0,3$, $P(B)=0,7$ et $P(A\cup B)=0,9$. Trouver $P(A\cap B)$, $P_{A}(B)$, $P_{B}(A)$
3. Soit B un événement tel que $P(B)\not =0$, montrer que $P_{B}(A)+P_{B}(\overline{A})=1$

Utiliser les formules de probabilités pour déterminer les probabilités inconnues

1. $P(A)=0,8$ et $P_{A}(B)=0,6$. Trouver $P(A\cap B)$
2. $P(A)=0,3$, $P(B)=0,7$ et $P(A\cup B)=0,9$. Trouver $P(A\cap B)$, $P_{A}(B)$, $P_{B}(A)$
3. Soit B un événement tel que $P(B)\not =0$, montrer que $P_{B}(A)+P_{B}(\overline{A})=1$

Utiliser les formules de probabilités pour déterminer les probabilités inconnues

1. $P(A)=0,8$ et $P_{A}(B)=0,6$. Trouver $P(A\cap B)$
2. $P(A)=0,3$, $P(B)=0,7$ et $P(A\cup B)=0,9$. Trouver $P(A\cap B)$, $P_{A}(B)$, $P_{B}(A)$
3. Soit B un événement tel que $P(B)\not =0$, montrer que $P_{B}(A)+P_{B}(\overline{A})=1$

On considère 2 événements $A$ et $B$ et l'arbre pondéré ci-dessous.

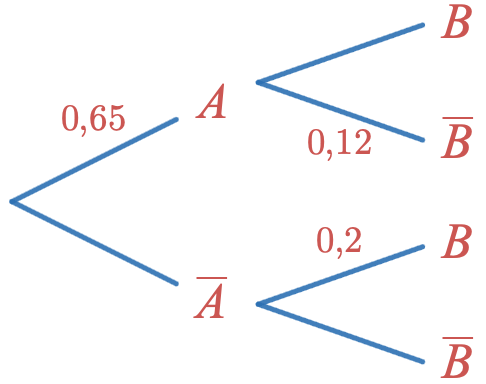
1. Compléter l'arbre pondéré ci-dessus
2. Quelle est la probabilité que B ne se réalise pas sachant que A ne réalise pas?
3. Déterminer la valeur de $P(B)$

Utiliser les formules de probabilités pour déterminer les probabilités inconnues

1. $P(A)=0,8$ et $P_{A}(B)=0,6$. Trouver $P(A\cap B)$
2. $P(A)=0,3$, $P(B)=0,7$ et $P(A\cup B)=0,9$. Trouver $P(A\cap B)$, $P_{A}(B)$, $P_{B}(A)$
3. Soit B un événement tel que $P(B)\not =0$, montrer que $P_{B}(A)+P_{B}(\overline{A})=1$

$A$, $B$ et $C$ sont 3 événements tels que:

1. $A$ et $B$ sont-ils indépendants? $A$ et $C$?
2. Quelle doit-être la valeur de $P(B \cap C)$ pour que $B$ et $C$ soient indépendants ?

Dans un sac, il y a:

1. 5 jetons verts numérotés de 1 à 5
2. 6 jetons blancs numérotés de 1 à 6
3. 4 jetons rouges numérotés de 1 à 4.

On prend au hasard un jeton dans le sac. On note

1. $U$ l’évènement « le jeton est numéroté 1 »
2. $V$ l’évènement « le jeton est vert »
3. $B$ l’évènement « le jeton est blanc »

1. $U$ et $V$ d'une part, et $U$ et $B$ d'autre part sont-ils indépendants?
2. $V$ et $B$ sont-ils indépendants?