Les exercices
sur 4 exercices complétés
On considère l'équation différentielle:$$(E):~y'=2y+cos(x)$$
- Déterminer deux nombres réels $a$ et $b$ tels que la fonction $f_0$ définie sur $\R$ par: $$f_{0}(x)=acos(x)+bsin(x)$$ soit une solution $f_0$ de $(E)$.
- Résoudre l'équation différentielle $(E_0):~y'=2y$.
- Démontrer que $f$ est solution de $(E)$ si et seulement si $f-f_0$ est solution de $(E_0)$.
- En déduire les solutions de $(E)$.
- Déterminer la solution $k$ de $(E)$ vérifiant $k(\frac{\pi}{2})=0$.
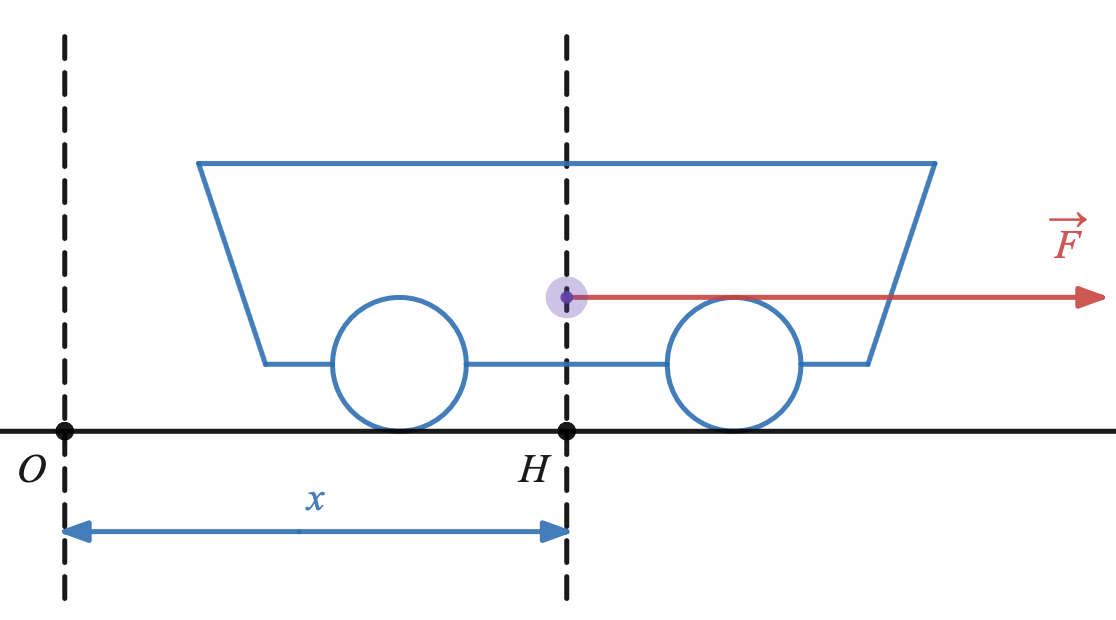
Un chariot de masse 200 kg se déplace sur une voie rectiligne et horizontale. Il est soumis à une force d'entraînement constante $\vec{F}$ de valeur 50 N.
Les forces de frottement sont proportionnelles à la vitesse et de sens contraire; le coefficient de proportionnalité a pour valeur absolue $25~N.m^{-1}.s$.
La position du chariot est repérée par la distance $x$, en mètres, du point $H$ à l'origine $O$ du repère en fonction du temps $t$, exprimé en secondes. On prendra $t$ dans l'intervalle $[0;~+\infin[$. Les lois de Newton conduisent à l'équation différentielle du mouvement:
$$(E)~~25x'+200x''=50,~où$$
$x'$ est la dérivé de $x$ par rapport au temps $t$,
$x''$ est la dérivé seconde de $x$ par rapport au temps $t$.
- On note $v(t)$ la vitesse du chariot au temps $t$; on rappelle que $v(t)=x'(t)$.
Prouver que $x$ est solution de $(E)$ si et seulement si $x'$ est solution de l'équation différentielle $$(F)~~v'=-\dfrac{1}{8}v+\dfrac{1}{4}$$ -
On suppose que, à l'instant $t=0$, on a: $x(0)=0$ et $x'(0)=0$.
- Calculer, pour tout nombre réel $t$ positif, $x'(t)$.
- En déduire que l'on a, pour tout nombre réel $t$ positif:$$x(t)=2t-16+16e^{\frac{-t}{8}}$$
- Calculer $V=\lim\limits_{t \to +\infin }v(t)$. Pour quelles valeurs de $t$ la vitesse du chariot est-elle inférieure ou égale à $90%$ de sa valeur limite $V$?
- Quelle est la distance parcourue par le chariot au bout de 30 secondes? On exprimera cette distance en mètres, au décimètre près.
On considère la fonction $f$ définie par:$$f(x)=\dfrac{x^2+2x+5}{x^2-3x+2}$$
- Montrer que $x^2-3x+2=(x-1)(x-2)$
- Déterminer deux nombres réels $a$ et $b$ tels que:$$f(x)=1+\dfrac{a}{x-1}+\dfrac{b}{x-2}$$
- Déterminer une primitive de $f$ sur $]-1;~+\infin[$.
- En utilisant cette méthode, déterminer une primitive de la fonction $g(x)=\dfrac{1}{x^2-1}$ sur l'intervalle $]1;~+\infin[$
Soit $g(x)$ le nombre, exprimé en millions, de personnes qui possèdent un smartphone.
On pose $x=0$ en 2008, $g(0)=1$ et $g$ est une solution qui ne s'annule pas sur $[0;~+\infin[$, de l'équation différentielle:
$$(E):~y'=\dfrac{1}{20}y(10-y)$$
- On considère une fonction $y$ qui ne s'annule pas sur $[0;~+\infin[$ et on pose $z=\dfrac{1}{y}$
- Montrer que $y$ est solution de $(E)$ si et seulement si $z$ est solution de l'équation différentielle: $$(E_1):~~z'=-\dfrac{1}{2}z+\dfrac{1}{20}$$
- Résoudre l'équation $(E_1)$ et en déduire les solutions de l'équation $(E)$.
- Montrer que $g$ est définie sur $[0;~+\infin[$ par $g(x)=\dfrac{10}{9e^{-\frac{1}{2}x}+1}$.
- Étudier les variations de $g$ sur $[0;~+\infin[$.
- Calculer la limite de $g$ en $+\infin$ et interpréter le résultat.
- En quelle année selon ce modèle le nombre de personnes possédant un smartphone dépassera-t'il 5 millions?
Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire
Primitives et équations différentielles
Fiche de synthèse
Contenu Complet Premium
Pour accéder au contenu complet de cette fiche de cours, vous devez vous abonner à notre offre premium.
Avec l'abonnement premium :
- Fiches de cours complètes
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Vidéos explicatives détaillées


