Contrôles d'entraînement
sur 2 exercices complétés
Le directeur d'une grande entreprise a proposé à l'ensemble de ses salariés un stage de formation à l'utilisation d'un nouveau logiciel.
Ce stage a été suivi par 25% des salariés.
- Dans cette entreprise, 52% des salariés de l'entreprise sont des femmes, parmi lesquelles 40% ont suivi le stage.
On interroge au hasard un salarié de l'entreprise et on considère les événements:
$F$: "le salarié interrogé est une femme"
$S$: "le salarié interrogé a suivi le stage"
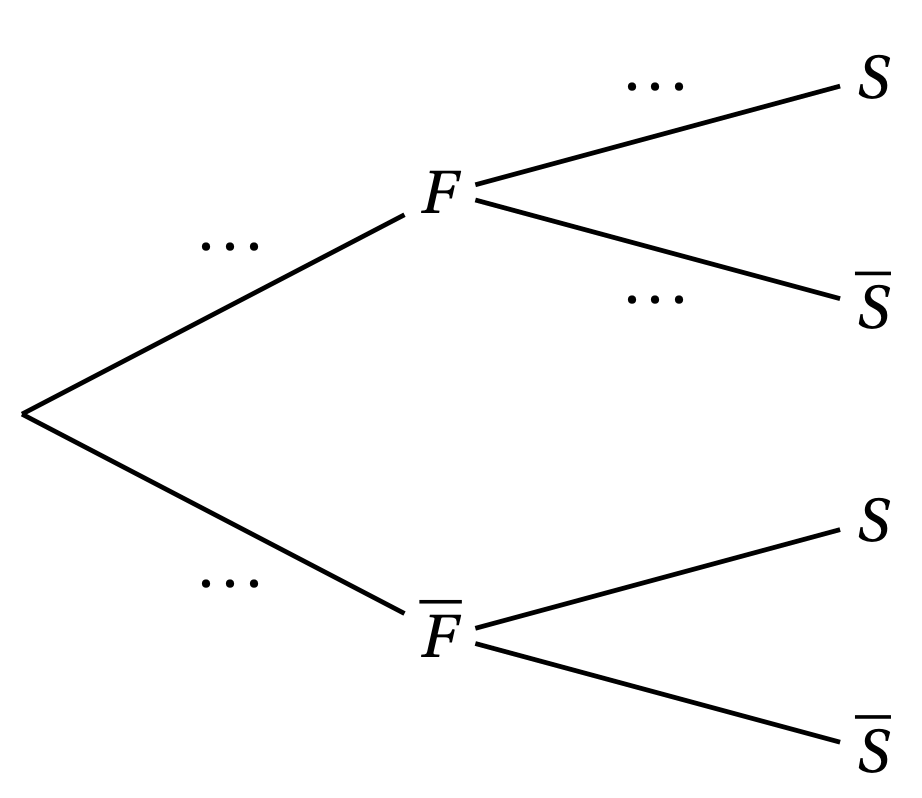
$F$ et $S$ désignent respectivement les événements contraires des événements $F$ et $S$. - Donner la probabilité de l'événement $S$
- Recopier et compléter les pointillés de l'arbre pondéré sur les branches indiquées.
- Démontrer que la probabilité que la personne interrogée soit une femme ayant suivi le stage est égale à $0,208$
- On sait que la personne interrogée a suivi le stage. Quelle est la probabilité que ce soit une femme?
- Le directeur affirme que, parmi les hommes salariés de l'entreprise, moins de 10% ont suivi le stage. Justifier l'affirmation du directeur
- On note $X$ la variable aléatoire qui à un échantillon de 20 salariés de cette entreprise choisis au hasard associe le nombre de salariés de cet échantillon ayant suivi le stage. On suppose que l'effectif des salariés de l'entreprise est suffisamment important pour assimilier ce choix à un tirage avec remise.
- Déterminer en justifiant la loi de probabilité suivie par la variable aléatoire $X$
- Déterminer à $10^{-3}$ près la probabilité que 5 salariés dans un échantillon de 20 aient suivi le stage.
- Le programme ci-dessous écrit en langage Python utilise la fonction binomiale$(i,n,p)$ créée pour l'occasion qui renvoie la valeur de la probabilité $P(X=i)$ dans le cas où la variable aléatoire $X$ suit une loi binomiale de paramètres $n$ et $p$.
- Déterminer à $10^{-3}$ près la probabilité qu'au moins 6 salariés dans un échantillon de 20 aient suivi le stage.

Déterminer à $10^{-3}$ près la valeur renvoyée par ce programme lorsque l'on saisit $proba(5)$ dans la console Python.
Interpréter cette valeur dans le contexte de l'exercice
Une société de jeu en ligne propose une nouvelle application pour smartphone nommée « Tickets coeurs ! ».
Chaque participant génère sur son smartphone un ticket comportant une grille de taille 3×3 sur laquelle sont placés trois cœurs répartis au hasard, comme par exemple ci-dessous.

Le ticket est gagnant si les trois cœurs sont positionnés côte à côte sur une même ligne, sur une même colonne ou sur une même diagonale.
- Justifier qu’il y a exactement 84 façons différentes de positionner les trois cœurs sur une grille.
- Montrer que la probabilité qu’un ticket soit gagnant est égale à $\dfrac{2}{21}$
- Lorsqu’un joueur génère un ticket, la société prélève 1€ sur son compte en banque. Si le ticket est gagnant, la société verse alors au joueur 5€. Le jeu est-il favorable au joueur ?
- Un joueur décide de générer 20 tickets sur cette application.On suppose que les générations des tickets sont indépendantes entre elles.
- Donner la loi de probabilité de la variable aléatoire $X$ qui compte le nombre de tickets gagnants parmi les 20 tickets générés.
- Calculer la probabilité, arrondie à $10^{-3}$, de l’évènement $(X=5)$.
- Calculer la probabilité, arrondie à $10^{-3}$, de l’évènement $(X\geq 1)$ et interpréter le résultat dans le contexte de l’exercice.
Lors d’une kermesse, un organisateur de jeux dispose, d’une part, d’une roue comportant quatre cases blanches et huit cases rouges et, d’autre part, d’un sac contenant cinq jetons portant les numéros $1$, $2$, $3$, $4$ et $5$.
Le jeu consiste à faire tourner la roue, chaque case ayant la même probabilité d’être obtenue, puis à extraire un ou deux jetons du sac selon la règle suivante :
- si la case obtenue par la roue est blanche, alors le joueur extrait un jeton du sac ;
- si la case obtenue par la roue est rouge, alors le joueur extrait successivement et sans remise deux jetons du sac.
Le joueur gagne si le ou les jetons tirés portent tous un numéro impair.
-
Un joueur fait une partie et on note $B$ l’évènement « la case obtenue est blanche », $R$ l’évènement « la case obtenue est rouge » et $G$ l’évènement « le joueur gagne la partie ».
- Donner la valeur de la probabilité conditionnelle $P_B(G)$.
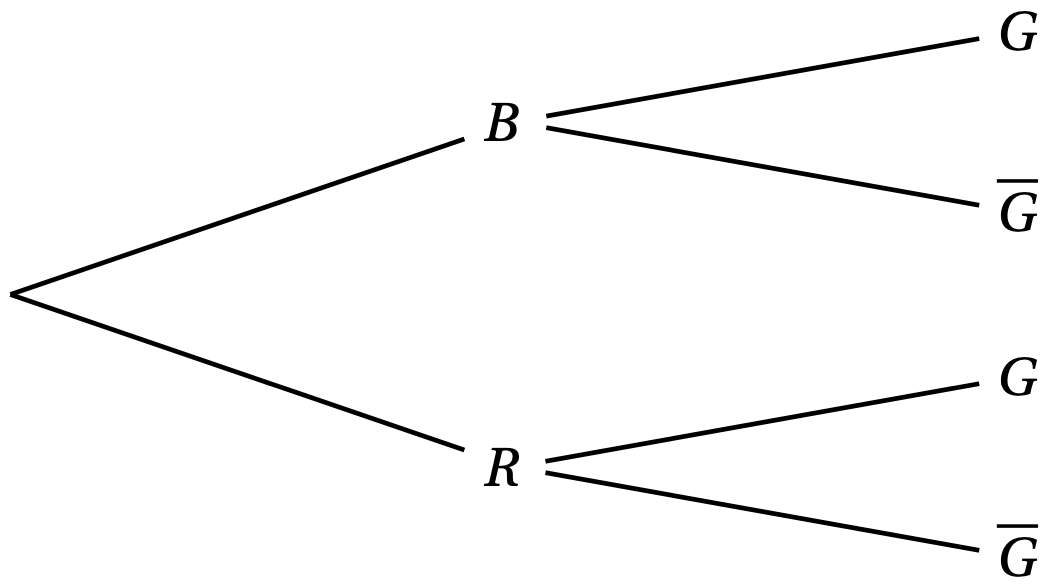
- On admettra que la probabilité de tirer successivement et sans remise deux jetons impairs est égale à $0,3$. Recopier et compléter l’arbre de probabilité suivant :
-
- Montrer que $P(G) = 0,4$.
- Un joueur gagne la partie. Quelle est la probabilité qu’il ait obtenu une case blanche en lançant la roue ?
- Les évènements $B$ et $G$ sont-ils indépendants ? Justifier.
-
Un même joueur fait dix parties. Les jetons tirés sont remis dans le sac après chaque partie. On note $X$ la variable aléatoire égale au nombre de parties gagnées.
- Expliquer pourquoi $X$ suit une loi binomiale et préciser ses paramètres.
- Calculer la probabilité, arrondie à $10^{-3}$ près, que le joueur gagne exactement trois parties sur les dix parties jouées.
- Calculer $P(X \geq 4)$ arrondie à $10^{-3}$ près. Donner une interprétation du résultat obtenu.
-
Un joueur fait $n$ parties et on note $p_n$ la probabilité de l’évènement « le joueur gagne au moins une partie ».
- Montrer que $p_n = 1 - 0,6^n$.
- Déterminer la plus petite valeur de l’entier $n$ pour laquelle la probabilité de gagner au moins une partie est supérieure ou égale à $0,99$.
Une chaîne de fabrication produit des pièces mécaniques. On estime que $4\%$ des pièces produites par cette chaîne sont défectueuses.
On choisit au hasard $n$ pièces produites par la chaîne de fabrication.
Le nombre de pièces produites est suffisamment grand pour que ce choix puisse être assimilé à un tirage avec remise.
On note $X$ la variable aléatoire égale au nombre de pièces défectueuses tirées.
Dans les trois questions suivantes, on prend $n = 50$.
- Quelle est la probabilité, arrondie au millième, de tirer au moins une pièce défectueuse?
- 1
- 0,870
- 0,600
- 0,599
- La probabilité $p(3 < X \leq 7)$ est égale à :
- $p(X \leq 7) - p(X > 3)$
- $p(X \leq 7) - p(X \leq 3)$
- $p(X < 7) - p(X > 3)$
- $p(X < 7) - p(X \leq 3)$
- Quel est le plus petit entier naturel $k$ tel que la probabilité de tirer au plus $k$ pièces défectueuses soit supérieure ou égale à $95\%$?
- 2
- 3
- 4
- 5
- Quelle est la probabilité de ne tirer que des pièces défectueuses?
- $0,04^n$
- $0,96^n$
- $1 - 0,04^n$
- $1 - 0,96^n$
- On considère la fonction Python ci-dessous. Que renvoie-t-elle?
def seuil(x): n = 1 while 1 - 0.96**n < x: n = n + 1 return n- Le plus petit nombre $n$ tel que la probabilité de tirer au moins une pièce défectueuse soit supérieure ou égale à $x$.
- Le plus petit nombre $n$ tel que la probabilité de ne tirer aucune pièce défectueuse soit supérieure ou égale à $x$.
- Le plus grand nombre $n$ tel que la probabilité de ne tirer que des pièces défectueuses soit supérieure ou égale à $x$.
- Le plus grand nombre $n$ tel que la probabilité de ne tirer aucune pièce défectueuse soit supérieure ou égale à $x$.
Dans les questions suivantes, $n$ ne vaut plus nécessairement $50$.
Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire
Loi binomiale
Fiche de synthèse
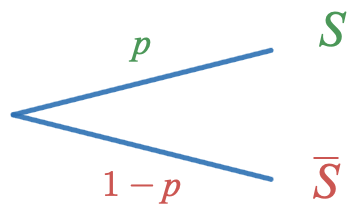
Loi Binomiale
| $k$ | $1$ | $0$ |
| $P(X=k)$ | $p$ | $1-p$ |
Contenu Complet Premium
Pour accéder au contenu complet de cette fiche de cours, vous devez vous abonner à notre offre premium.
Avec l'abonnement premium :
- Fiches de cours complètes
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Vidéos explicatives détaillées


