Les exercices
sur 6 exercices complétés
Soit $X$ une variable aléatoire qui suit la binomiale $B(22; 0,13)$. Calculer les probabilités suivantes en détaillant la démarche.
- $P_{X\geq 4}(X<12)$
- $P_{X<11}(X=7)$
- $P_{8\leq X\leq 15}(X<17)$
- $P_{X<21}(16\leq X\leq 19)$
- $P_{X\leq 5}(X>6)$
Chaque jour dans une classe de 25 élèves chaque élève arrive en retard indépendamment des autres avec probabilité 0,08. On s'intéresse au nombre d'élèves en retard. Soit $X$ la variable aléatoire qui compte le nombre d'élèves en retard un certain jour.
- Déterminer la loi suivie par $X$ et préciser ses paramètres
- Calculer l'espérance de $X$ et interpréter
- Quelle est la probabilité que 2 élèves soient en retard?
- Quelle est la probabilité qu'au moins 1 élève soit en retard?
- Quelle est la probabilité qu'au maximum 4 élèves soient en retard?
On lance simultanément 2 dés non truqués à 6 faces. On s'intéresse à la somme des 2 chiffres obtenus.
- Si on fait 1 lancer des 2 dés, quelle est la probabilité d'obtenir une somme supérieure ou égale à 9?
- Au bout de 15 lancers quelle est la probabilité d'avoir obtenu 10 fois un total supérieur ou égal à 10?
- Au bout de 20 lancers quelle est la probabilité d'avoir obtenu 10 fois un total compris entre 4 et 6?
Le programme Python ci-dessous permet de simuler une expérience aléatoire. Déterminer à partir de ce programme la loi suivie par la variable aléatoire $X$ et préciser ses paramètres

On choisit $n$ personnes au hasard (avec $n$ un entier naturel non nul) dans une population, et on assimile ces tirages à des tirages indépendants avec remise. La probabilité qu'une personne soit gauchère est de 12%.
- Exprimer en fonction de $n$ la probabilité $p_n$ d'avoir au moins 1 gaucher dans le groupe de $n$ personnes.
- On cherche le plus petit entier $n$ tel que $p_n \geq 0,99$. Interpréter cette inégalité avec une phrase.
- Écrire un algorithme Python qui détermine le plus petit entier $n$ tel que $p_n \geq 0,99$
- Déterminer cette valeur avec la calculatrice
La loi de probabilité d'une variable aléatoire qui suit la loi binomiale est donnée ci-dessous.

- Calculer la probabilité manquante
- Calculer $E(X)$
- Calculer $P(X\geq 4)$
- Peut-on affirmer que $P_{X\leq 3}(X\geq 2)=0,631$?
- Déterminer les paramètres de cette loi binomiale
Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire
Loi binomiale
Fiche de synthèse
Loi Binomiale
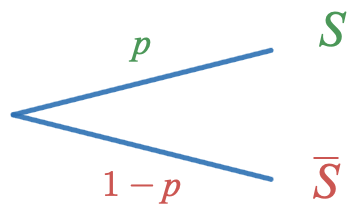
| $k$ | $1$ | $0$ |
| $P(X=k)$ | $p$ | $1-p$ |
Contenu Complet Premium
Pour accéder au contenu complet de cette fiche de cours, vous devez vous abonner à notre offre premium.
Avec l'abonnement premium :
- Fiches de cours complètes
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Vidéos explicatives détaillées


