Les exercices
Un sac contient 4 jetons blancs et 8 jetons noirs. On tire successivement et avec remise 2 jetons dans le sac. Le jeu consiste à tirer 2 jetons de couleur différente.
- Quelle est la probabilité de gagner une partie?
- Quelle est la loi de probabilité de $X$?
- Exprimer $p_n$ en fonction de $n$
- Quel est le nombre minimal de parties à jouer afin que $p_n \geq 0,99$
- Ecrire un programme Python qui permet de trouver la valeur de la question précédente
On joue $n$ fois de suite à ce jeu, avec $n$ qui est un nombre entier tel que $n\geq 2$.
On note $p_n$ la probabilité de gagner au moins une partie sur le total des $n$ jouées, et $X$ la variable aléatoire qui compte le nombre de parties gagnées.
On lance une pièce de monnaie équilibrée $n$ fois. On note $X$ le nombre de "Face" obtenues.
- Quelle est la loi suivie par $X$?
- On lance la pièce $n$ fois. Montrer que $P(A)=\frac{n}{2^{n-1}}$
- Déterminer la probabilité d'obtenir exactement 1 Face ou 1 Pile sur 5, 10 puis 15 lancers
- Conjecturer ce qu'il se passe quand on lance la pièce un grand nombre de fois
On s'intéresse à l'événement $A$: "obtenir exactement 1 Face ou 1 Pile"
Un constructeur de voitures a 3 fournisseurs de pneus: il achète 30% de ses pneus au fournisseur A, 40% au fournisseur B et le reste au fournisseur C.
80% des pneus du fournisseur A sont sans défaut, 95% pour B et 85% pour C.
Le constructeur choisit un pneu au hasard.
- Construire l'arbre pondéré qui traduit cette situation
- Montrer que la probabilité que le pneu soit sans défaut est 0,875
- On sait que le pneu choisi est sans defaut. Quelle est la probabilité qu'il vienne du fournisseur C?
- Quelle est la probabilité qu'au plus un des pneus soit défectueux?
On choisit 12 pneus au hasard. On assimile ces tirages à des tirages avec remise.
Une urne contient des jetons blancs et noirs tous indiscernables au toucher.
Une partie consiste à prélever au hasard successivement et avec remise deux jetons de cette urne.
On établit la règle de jeu suivante :
- un joueur perd 9 euros si les deux jetons tirés sont de couleur blanche ;
- un joueur perd 1 euro si les deux jetons tirés sont de couleur noire ;
- un joueur gagne 5 euros si les deux jetons tirés sont de couleurs différentes.
-
On considère que l’urne contient 2 jetons noirs et 3 jetons blancs.
- Modéliser la situation à l’aide d’un arbre pondéré.
- Calculer la probabilité de perdre 9 € sur une partie.
-
On considère maintenant que l’urne contient 3 jetons blancs et au moins deux jetons noirs mais on ne connaît pas le nombre exact de jetons noirs. On appellera $N$ le nombre de jetons noirs.
- Soit $X$ la variable aléatoire donnant le gain du jeu pour une partie.
Déterminer la loi de probabilité de cette variable aléatoire. - Résoudre l’inéquation pour $x$ réel : $$ -x^2 + 30x - 81 > 0 $$
- En utilisant le résultat de la question précédente, déterminer le nombre de jetons noirs que l’urne doit contenir afin que ce jeu soit favorable au joueur.
- Combien de jetons noirs le joueur doit-il demander afin d’obtenir un gain moyen maximal ?
- Soit $X$ la variable aléatoire donnant le gain du jeu pour une partie.
-
On observe 10 joueurs qui tentent leur chance en effectuant une partie de ce jeu, indépendamment les uns des autres. On suppose que 7 jetons noirs ont été placés dans l’urne (avec 3 jetons blancs).
Quelle est la probabilité d’avoir au moins 1 joueur gagnant 5 euros ?
Un commerçant vend deux types de matelas : matelas RESSORTS et matelas MOUSSE.
On suppose que chaque client achète un seul matelas.
On dispose des informations suivantes :
- 20 % des clients achètent un matelas RESSORTS. Parmi eux, 90 % sont satisfaits de leur achat.
- 82 % des clients sont satisfaits de leur achat.
Les deux parties peuvent être traitées de manière indépendante.
Partie A
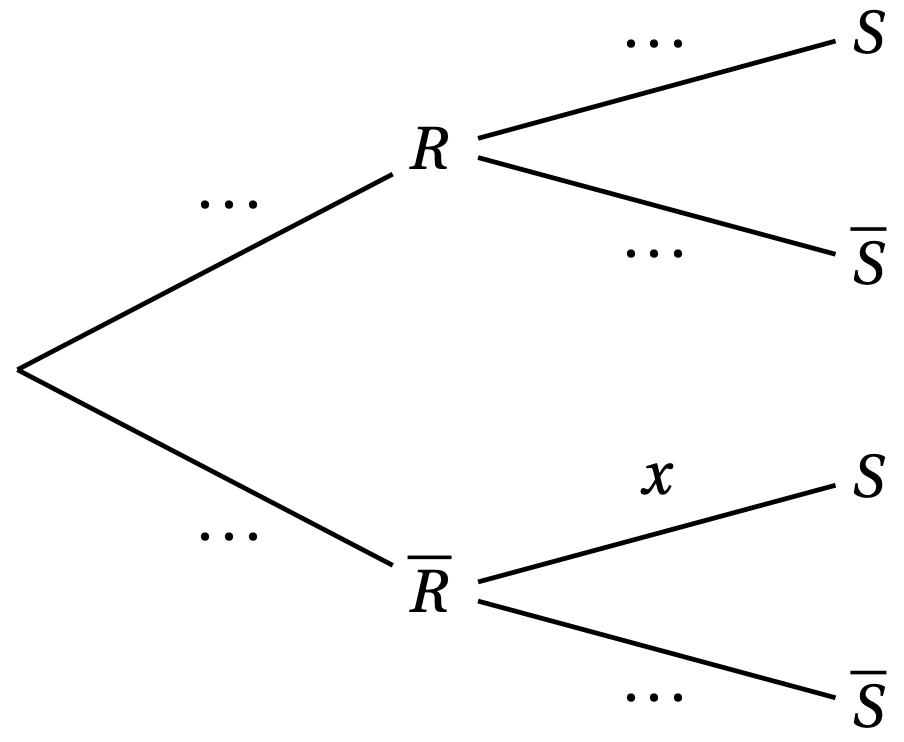
On choisit au hasard un client et on note les évènements :
- $R$ : « le client achète un matelas RESSORTS »
- $S$ : « le client est satisfait de son achat »
On note $x = P_{\overline{R}}(S)$, où $P_{\overline{R}}(S)$ désigne la probabilité de $S$ sachant que $R$ n’est pas réalisé.
- Recopier et compléter l’arbre pondéré ci-contre décrivant la situation.
- Démontrer que $x = 0,8$.
- On choisit un client satisfait de son achat. Quelle est la probabilité qu’il ait acheté un matelas RESSORTS ?
On arrondira le résultat à $10^{-2}$.
Partie B
-
On choisit 5 clients au hasard. On considère la variable aléatoire $X$ qui donne le nombre de clients satisfaits de leur achat parmi ces 5 clients.
- On admet que $X$ suit une loi binomiale. Donner ses paramètres.
- Déterminer la probabilité qu’au plus trois clients soient satisfaits de leur achat.
On arrondira le résultat à $10^{-3}$.
-
Soit $n$ un entier naturel non nul. On choisit à présent $n$ clients au hasard. Ce choix peut être assimilé à un tirage au sort avec remise.
- On note $p_n$ la probabilité que les $n$ clients soient tous satisfaits de leur achat. Démontrer que $p_n = 0,82^n$.
- Déterminer les entiers naturels $n$ tels que $p_n < 0,01$. Interpréter dans le contexte de l’exercice.
Les deux parties de cet exercice sont indépendantes.
Dans une grande ville française, des trottinettes électriques sont mises à disposition des usagers. Une entreprise, chargée de l’entretien du parc de trottinettes, contrôle leur état chaque lundi.
Partie A
On estime que :
- lorsqu’une trottinette est en bon état un lundi, la probabilité qu’elle soit encore en bon état le lundi suivant est $0,9$ ;
- lorsqu’une trottinette est en mauvais état un lundi, la probabilité qu’elle soit en bon état le lundi suivant est $0,4$.
On s’intéresse à l’état d’une trottinette lors des phases de contrôle.
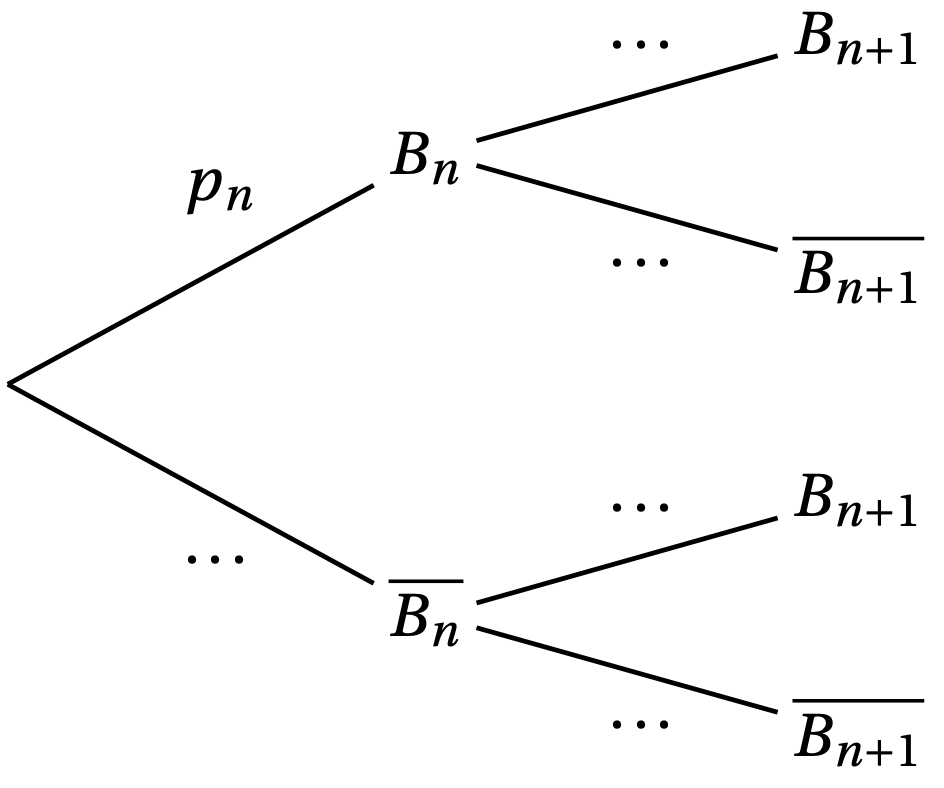
Soit $n$ un entier naturel. On note $B_n$ l’évènement « la trottinette est en bon état $n$ semaines après sa mise en service » et $p_n$ la probabilité de $B_n$.
Lors de sa mise en service, la trottinette est en bon état. On a donc $p_0 = 1$.
- Donner $p_1$ et montrer que $p_2 = 0,85$. On pourra s’appuyer sur un arbre pondéré.
- Recopier et compléter l’arbre pondéré ci-dessous :
- En déduire que, pour tout entier naturel $n$, $p_{n+1} = 0,5p_n + 0,4$.
-
- Démontrer par récurrence que pour tout entier naturel $n$, $p_n \geq 0,8$.
- À partir de ce résultat, quelle communication l’entreprise peut-elle envisager pour valoriser la fiabilité du parc ?
-
- On considère la suite $(u_n)$ définie pour tout entier naturel $n$ par $u_n = p_n - 0,8$. Montrer que $(u_n)$ est une suite géométrique dont on donnera le premier terme et la raison.
- En déduire l’expression de $u_n$ puis de $p_n$ en fonction de $n$.
- En déduire la limite de la suite $(p_n)$.
Partie B
Dans cette partie, on modélise la situation de la façon suivante :
- l’état d’une trottinette est indépendant de celui des autres ;
- la probabilité qu’une trottinette soit en bon état est égale à $0,8$.
On note $X$ la variable aléatoire qui, à un lot de $15$ trottinettes, associe le nombre de trottinettes en bon état.
Le nombre de trottinettes du parc étant très important, le prélèvement de $15$ trottinettes peut être assimilé à un tirage avec remise.
- Justifier que $X$ suit une loi binomiale et préciser les paramètres de cette loi.
- Calculer la probabilité que les $15$ trottinettes soient en bon état.
- Calculer la probabilité qu’au moins $10$ trottinettes soient en bon état dans un lot de $15$.
- On admet que $E(X) = 12$. Interpréter le résultat.