Les exercices
sur 7 exercices complétés
On considère l'expérience aléatoire suivante: on lance un dé à 6 faces plusieurs fois de suite, de façon identique et indépendante. On note le succès l'évenement: "obtenir un 6".
- Définir l'évenement qui correspond à l'échec dans cette épreuve de Bernoulli
- Représenter cette epreuve de Bernoulli par un arbre
- On lance désormais le dé 3 fois de suite: représenter la situation par un arbre
- Combien de chemins comprennent 2 succès? 1 succès? 0 et 3 succès?
- Déterminer la probabilité d'obtenir 2 fois un 6
On considère les expériences aléatoires ci-dessous. Pour chacune d'elles préciser s'il s'agit d'un schéma de Bernoulli.
- Une urne contient 8 boules indiscernables au toucher, 5 vertes et 3 rouges. On tire successivement et avec remise 4 boules. On s'intéresse au nombre de boules rouges tirées.
- On tire successivement avec remise 3 cartes dans un jeu de 52 cartes. On s'intéresse à la valeur des cartes tirées
- On tire 5 fois de suite une pièce non équilibrée avec probabilité d'obtenir pile 0,7. On s'intéresse au nombre total de faces obtenues.
- On tire successivement 2 chocolats sans les remettre dans une boite qui contient 4 chocolats noirs et 4 chocolats au lait. On compte le nombre de chocolats noirs obtenus.
On considère $X$ une variable aléatoire qui suit la loi binomiale de paramètres 15 et 0,28.
- Exprimer $P(X=0)$ et déterminer sa valeur
- Exprimer $P(X=6)$ et déterminer sa valeur
- Exprimer $P(X\geq 1)$ en fonction de $P(X=0)$ et déterminer sa valeur
- Exprimer $P(X\geq 14)$ et déterminer sa valeur
- Exprimer $P(12\leq X\leq 13)$ et déterminer sa valeur
Un sac contient 100 jetons indiscernables au toucher dont 42 sont verts et 58 sont bleus. On prend au hasard un jeton, on regarde sa couleur et on le replace dans le sac. On répète en tout 3 fois de suite cette expérience et on s'intéresse au nombre de jetons verts tirés.
- Expliquer pourquoi chaque tirage correspond à une epréuve de Bernoulli et construire le tableau de sa loi de probabilité
- Justifier que l'on peut associer un schéma de Bernoulli à cette expérience.
- Représenter ce schéma par un arbre pondéré
- En déduire la probabilité d'obtenir 3 jetons de la même couleur
Soit $X$ une variable aléatoire qui suit la loi binomiale $B(8; 0,45)$. Sur l'arbre pondéré modélisant cette loi, combien de chemins correspondent à:
- 1 succès
- 3 succès
- 8 succès
- Que représente $\binom{8}{2}$?
- Peut-on dire que $\binom{8}{0}=1$?
Soit $X$ une variable aléatoire qui suit la loi binomiale $B(20; 0,01)$.
- $P(X=0)+P(X=1)+P(X=2)+P(X=3)$
- $P((X>13)\cap (X\leq 17)$
- $P(X\geq 7)-P(X\geq 10)$
- $P(X=15)+P(X=16)+P(X=17)+P(X=18)+P(X=19)$
- $P(X\geq 14)+P(X=13)$
Chaque jour où il travaille Paul doit se rendre à la gare pour rejoindre son lieu de travail en train. Pour cela, il prend son vélo deux fois sur trois, et s'il ne prend pas
son vélo, il prend sa voiture.
Lorsqu'il prend son vélo, Paul ne rate le train qu'une fois sur 50, alors que s'il prend la voiture, il le rate une fois sur 10.
$V$: "Paul prend son vélo pour rejoindre la gare"
$R$: "Paul rate son train"
- Faire un arbre pondéré résumant la situation
- Montrer que la probabilité que Paul rate son train est égale à $\frac{7}{150}$
- Paul a raté son train. Déterminer la valeur exacte de la probabilité qu'il ait pris son vélo pour rejoindre la gare.
Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire
Loi binomiale
Fiche de synthèse
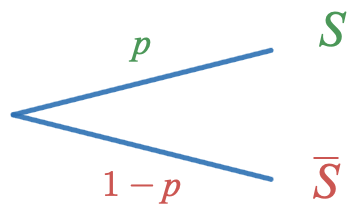
Loi Binomiale
| $k$ | $1$ | $0$ |
| $P(X=k)$ | $p$ | $1-p$ |
Contenu Complet Premium
Pour accéder au contenu complet de cette fiche de cours, vous devez vous abonner à notre offre premium.
Avec l'abonnement premium :
- Fiches de cours complètes
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Vidéos explicatives détaillées


