On considère les points suivants $E(4;-1;2)$, $F(1;3;-1)$, $G(2;-2;1)$

1. Montrer que les points $E$, $F$ et $G$ définissent un plan

Le but des questions suivantes est de déterminer ce que l'on appelle une équation paramétrique du plan $(EFG)$ (on connaît ce terme mais pour une droite).

2. Soit $H(x;y;z)$ un point de l'espace qui appartient au plan $(EFG)$.
1. Montrer qu'il existe 2 nombres réels $k$ et $k'$ tels que $\vec{EH}=k\vec{EF}+ k'\vec{EG}$
2. En déduire que $H \in (EFG)$ si et seulement si et seulement si $$\begin{cases}x=-3k-2k'+4\\ y=4k-k'-1\\ z=-3k-k'+2\end{cases}$$
3. $J(-1;~3;~6)$ est-il dans le plan $(EFG)$?
3. On considère le points $K(1;~9;~-16)$
1. Déterminer une représentation paramétrique de la droite $(JK)$
2. En utilisant un vecteur directeur de la droite $(JK)$ déterminer si cette droite est parallèle au plan $(EFG)$

Un artiste souhaite réaliser une sculpture composée d’un tétraèdre posé sur un cube de 6 mètres d’arête. Ces deux solides sont représentés par le cube ABCDEFGH et par le tétraèdre SELM ci-dessous.

On munit l’espace du repère orthonormé $(A; \vec{AI};\vec{AJ};\vec{AK})$ tel que: $I \in [AB]$, $J\in [AD]$, $K\in [AE]$ et $AI = AJ = AK = 1$, l’unité graphique représentant 1 mètre. Les points $L$, $M$ et $S$ sont définis de la façon suivante:

1. $L$ est le point tel que $\vec{FL}=\frac{2}{3}\vec{FE}$;
2. $M$ est le point d’intersection du plan $(BDL)$ et de la droite $(EH)$;
3. $S$ est le point d’intersection des droites $(BL)$ et $(AK)$

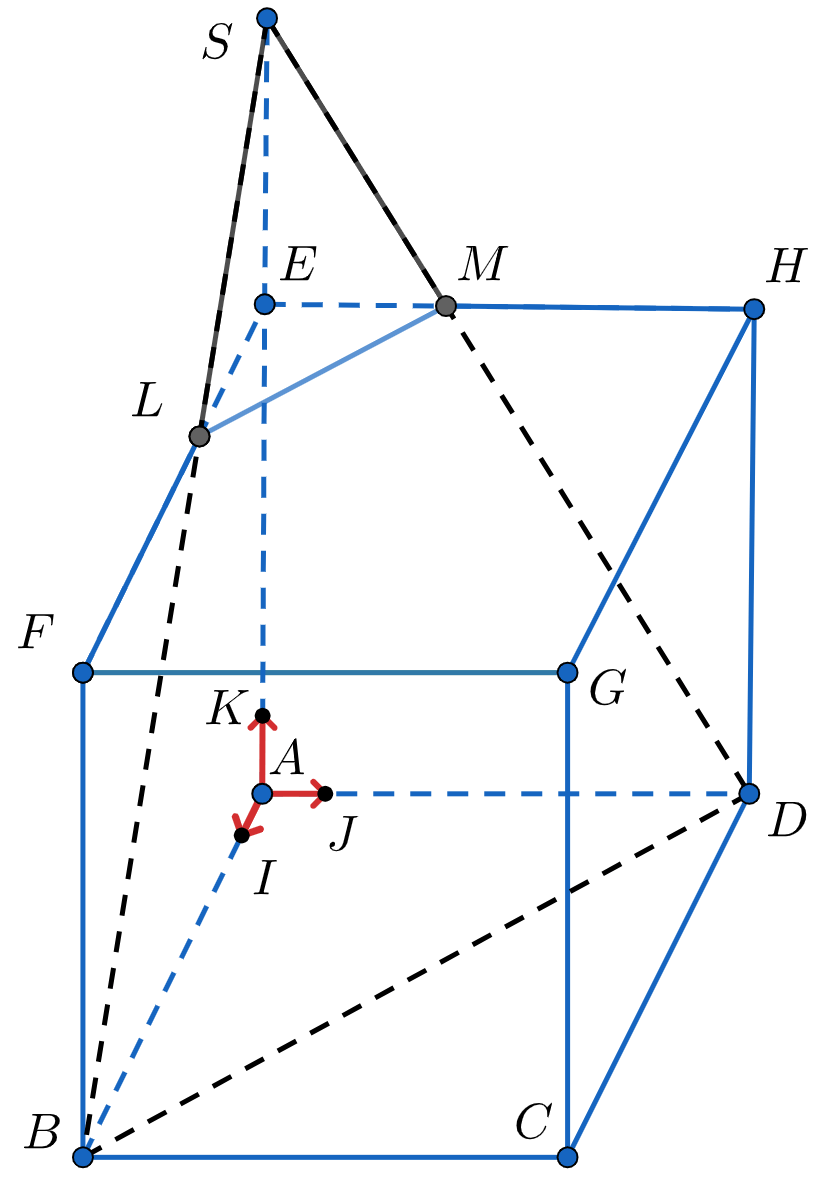
1. Démontrer, sans calcul de coordonnées, que les droites $(LM)$ et $(BD)$ sont parallèles.
2. Démontrer que les coordonnées du point $L$ sont $(2; 0; 6)$.
3. Donner une représentation paramétrique de la droite $(BL)$.
4. Vérifier que les coordonnées du point $S$ sont $(0; 0; 9)$.
5. Après avoir déterminé une représentation paramétrique de la droite $(SD)$ puis de la droite $(EH)$, en déduire les coordonnées du point $M$.