On considère une fonction $f$ de courbe représentative $C_f$.

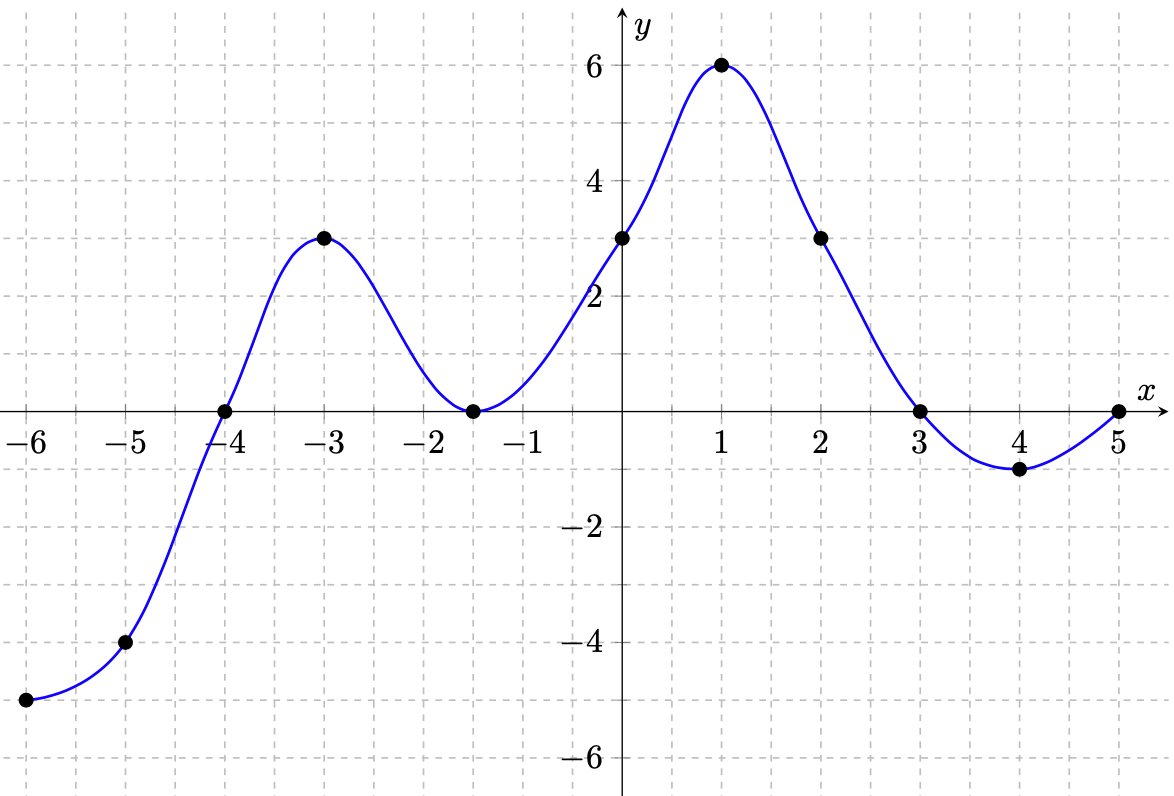
1. Déterminer le domaine de définition de $f$.
2. Déterminer l'image de $2$ par la fonction $f$.
3. Déterminer le(s) antécédent(s) de $0$ par $f$.
4. Quel est le nombre de solution de l'équation $f(x)=1$?
5. Déterminer le maximum et le minimum de la fonction $f$ sur son domaine de définition, ainsi que leur(s) antécédent(s).
6. Quel est l'ensemble des nombres réels qui ont une image inférieure ou égale à $0$?

Déterminer si les fonctions suivantes sont paires, impaires, ou aucun des deux.

1. $f(x)=x^3-x$
2. $g(x)=x^4-2x^2+1$
3. $h(x)=\dfrac{1}{x}+x^2$
4. $j(x)=\dfrac{x^5}{|x|}$
5. $k(x)=x^3+|x|$

Déterminer le domaine de définition des fonctions suivantes.

1. $f(x)=\sqrt{2x-5}$
2. $g(x)=\dfrac{x+1}{x^2-3}$
3. $h(x)=\sqrt{5-|x-1|}$
4. $j(x)=\dfrac{3x}{x^2-12x+36}$

On relève la fréquence cardiaque, en battements par minute (bpm), d’un sportif pendant un effort soutenu d’une durée de 14 minutes.
L’évolution de la fréquence cardiaque de ce sportif durant ces 14 minutes est modélisée par une fonction $f$ définie sur l’intervalle $[0;~14]$ : pour tout instant $t$, exprimé en minute, $f(t)$ représente la fréquence cardiaque du sportif à cet instant, exprimée en bpm. Dans le repère orthogonal ci-après, on a tracé la courbe représentative de la fonction $f$ sur l’intervalle $[0;~14]$.

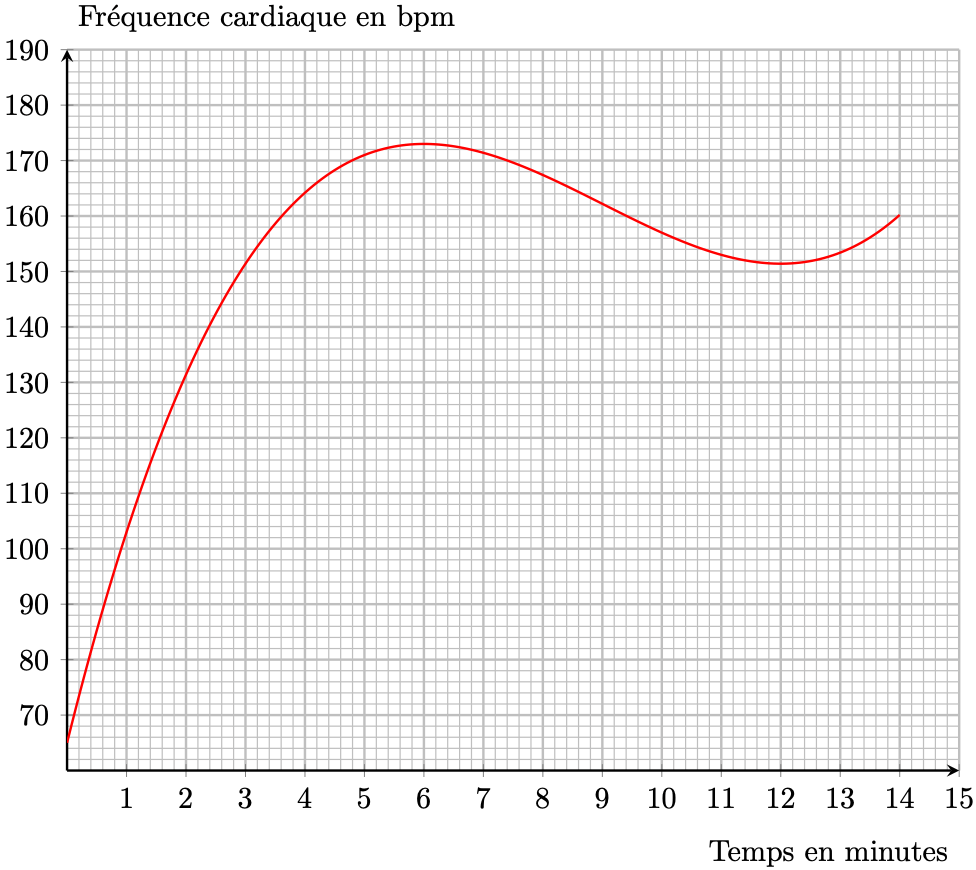
En utilisant cette modélisation, avec la précision permise par le graphique, répondre aux questions suivantes :

1. Au bout de combien de minutes la fréquence cardiaque est-elle maximale ? À combien de battements par minute s’élève-t-elle alors ?
2. Ce sportif est considéré comme étant en période d’effort intense lorsque sa fréquence cardiaque est supérieure ou égale à 165 bpm. Sur quel intervalle de temps a-t-il été en effort intense ?

On admet que pour tout $t \in [0;~14]$, $f(t) = 0,2t^3 - 5,4t^2 + 43,2t + 65$.

3. Calculer $f(2)$ et interpréter.

On donne le tableau de valeurs suivant.


4. A l'aide du tableau de valeurs, déterminer une valeur qui a deux antécédents.
5. A l'aide du tableau de valeurs, déterminer une valeur qui a deux antécédents.
6. A l'aide du tableau de valeurs et du graphique, résoudre l'inéquation $f(x)\geq 151.4$