Déterminer graphiquement:

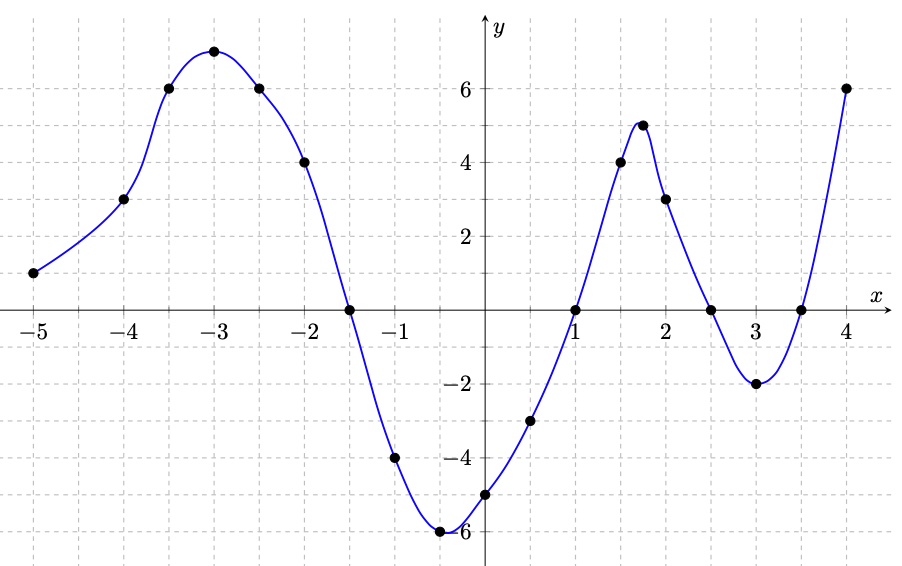
1. L'image de $-2$
2. Un antécédent de $3$
3. L'image de $-1$
4. Un antécédent de $0$
5. L'image de $2$
6. Le nombre d'antécédents de $0$

Déterminer le domaine de définition des fonctions suivantes.

1. $f(x)=\dfrac{5}{(x-3)(x+2)}$
2. $g(x)=\sqrt{1-4x}$
3. $h(x)=\dfrac{1}{\sqrt{x}}+5x-1$
4. $j(x)=2\sqrt{x^2+1}$
5. $k(x)=\dfrac{x+2}{\sqrt{x-1}}$

Des analyses ont montré que des microalgues étaient naturellement présentes dans l’eau de mer, avec une concentration normale comprise entre $0$ et $100$ milligrammes par litre $\text{(mg/L)}$. Ces microalgues ont tendance à se multiplier lorsque la salinité de l’eau de mer diminue, et les autorités sanitaires considèrent qu’elles deviennent dangereuses pour la santé lorsque leur concentration dépasse $200~\text{mg/L}$. Il faut alors prendre des mesures comme l’interdiction de la baignade. La courbe donnée en annexe modélise l’évolution de la concentration en microalgues de l’eau de baignade d’une plage du littoral pendant les 10 jours qui ont suivi un très fort orage. On modélise cette concentration par la fonction $f$ définie sur l'intervalle $[0;~10]$ par $f(x)=x^3 - 21x^2 + 120x + 50$.

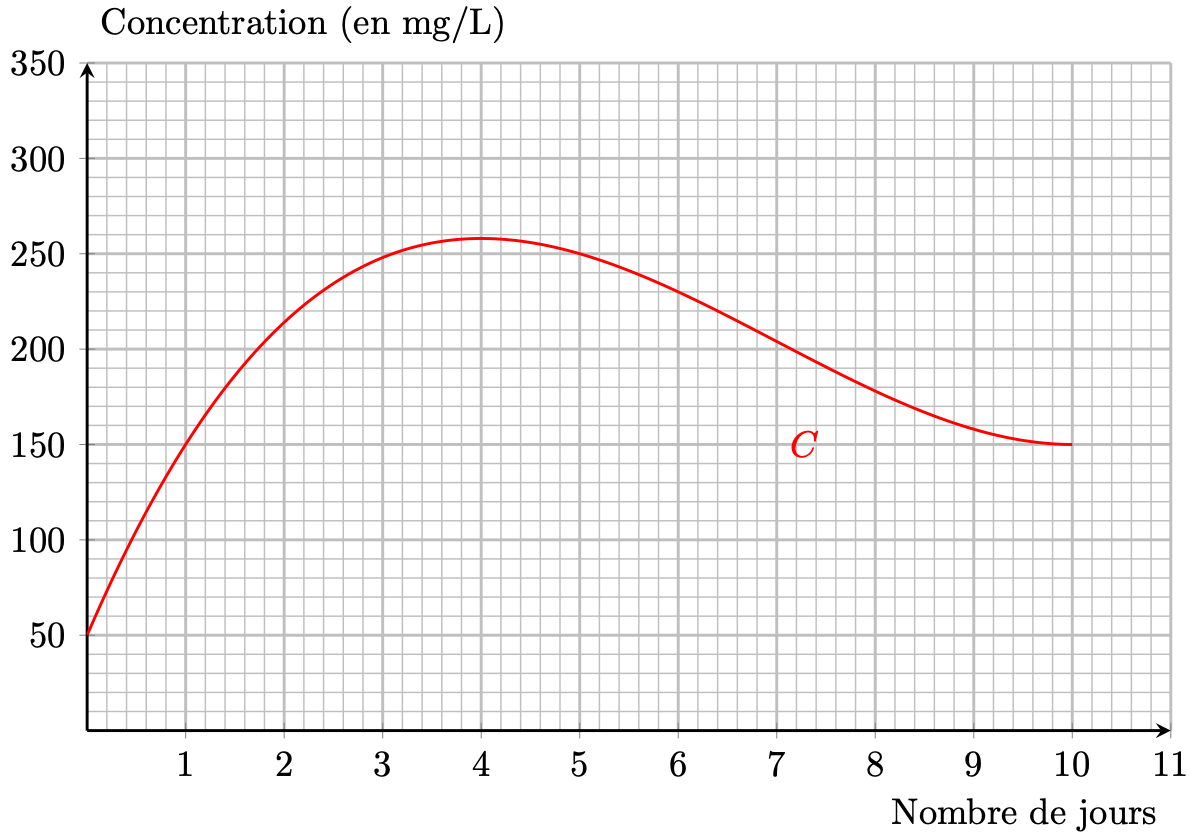
1. Pendant combien de jours complets la baignade est-elle interdite ?
2. Quelle est la concentration maximale en microalgues durant les 10 jours suivant l’orage ? Au bout de combien de jours a-t-elle été atteinte ?
3. Déterminer cette concentration maximale par le calcul.
4. Peut-on considérer que 10 jours après l’orage, la situation est revenue à la normale ?
5. L'équation $f(x)=150$ se ramène à résoudre $(x-10)^2(x-1)=0$. Que peut-on en déduire?