Les exercices
Exercice 1 - Déterminer une image par le calcul
Déterminer les images suivantes
- $f(1)$ pour $f(x)=1-3x$
- $g(-2)$ pour $g(x)=\frac{2+x}{3x-5}$
- $h(-3)$ pour $h(x)=2x-5x^2$
- $i(\frac{1}{4})$ pour $i(x)=\frac{3}{x}$
Gratuit
Exercice 2 - Déterminer un antécédent par le calcul
Déterminer le(s) antécédent(s) de:
- $-1$ par $f(x)=4x+3$
- $7$ par $g(x)=x^2-9$
- $5$ par $h(x)=2+\frac{1}{x}$
- $-2$ par $i(x)=\frac{2x+5}{-x+2}$
Exercice 3 - Déterminer si un point appartient à la courbe d'une fonction par le calcul
Déterminer si les points suivants appartiennent aux courbes:
- $A(0;3)$ à $C_{f}$ avec $f(x)=4x+3$
- $B(-1;5)$ à $C_{g}$ avec $g(x)=7x^2-3$
- $C(\frac{1}{2};9)$ à $C_{h}$ avec $h(x)=\frac{4}{x}+2x$
- $D(-2;0)$ à $C_{i}$ avec $i(x)=-x^2-3x-2$
Exercice 4 - Déterminer images et antécédents graphiquement
Déterminer graphiquement:
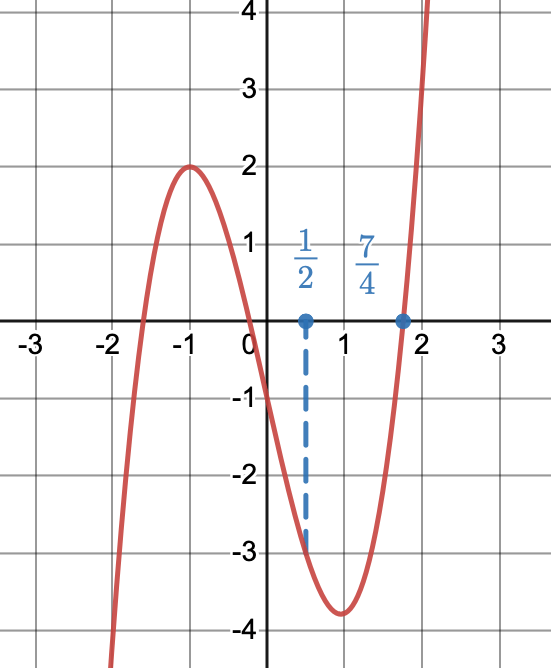
- L'image de $-2$
- Un antécédent de $3$
- L'image de $-1$
- Un antécédent de $0$
- L'image de $2$
- Le nombre d'antécédents de $0$
Exercice 5 - Déterminer des coordonnées par le calcul
Soit $f$ la fonction définie par $f(x)=x^2-3x-1$
- $A$ est le point de $C_{f}$ d'abscisse $5$, quelle est son ordonnée?
- $B$ est le point $C_{f}$ d'ordonnée $-1$, quelles sont les abscisses possibles?
- $D(4;11)$ appartient-il à $C_{f}$?
Exercice 6 - Fonctions et tableau de valeurs
On considère une fonction $f$ définie sur $[-2;5]$ dont un tableau de valeurs est donné ci-dessous
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ | $3$ | $4$ | $5$ |
| $f(x)$ | $4$ | $-1$ | $-2$ | $7$ | $0$ | $-3$ | $1$ | $0$ |
- Un antécédent de $-1$ par $f$ est:
- L'image de $0$ par $f$ vaut:
- $D(4;11)$ appartient-il à $C_{f}$?
