Déterminer si les fonctions suivantes sont paires, impaires ou ni paires ni impaires.

1. $f(x)=1-x^2$
2. $g(x)=x^3-5x$
3. $h(x)=\dfrac{2x}{1+x}$
4. $k(x)=\dfrac{5}{x}+sin(x)$

Déterminer si les fonctions suivantes sont paires, impaires ou ni paires ni impaires.

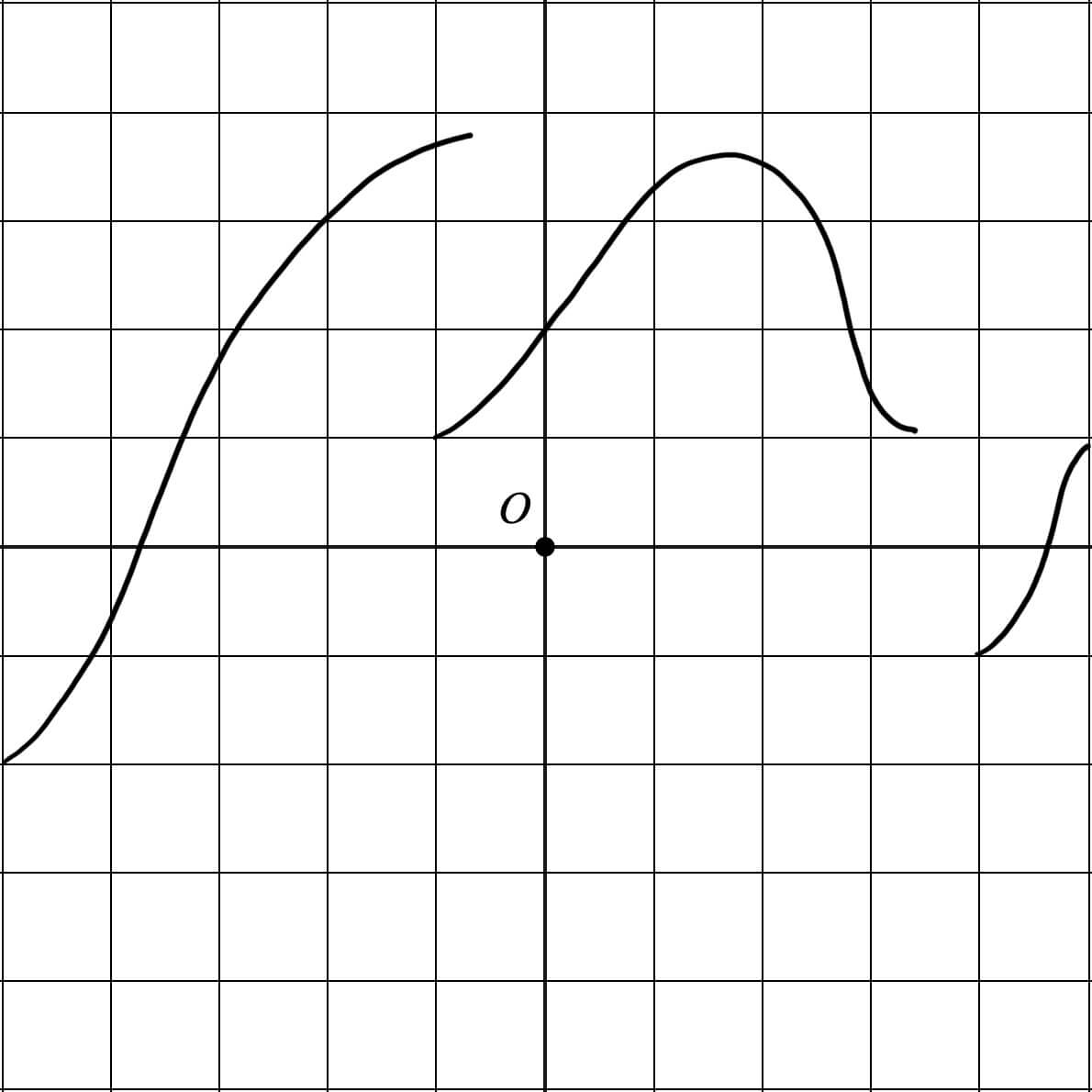
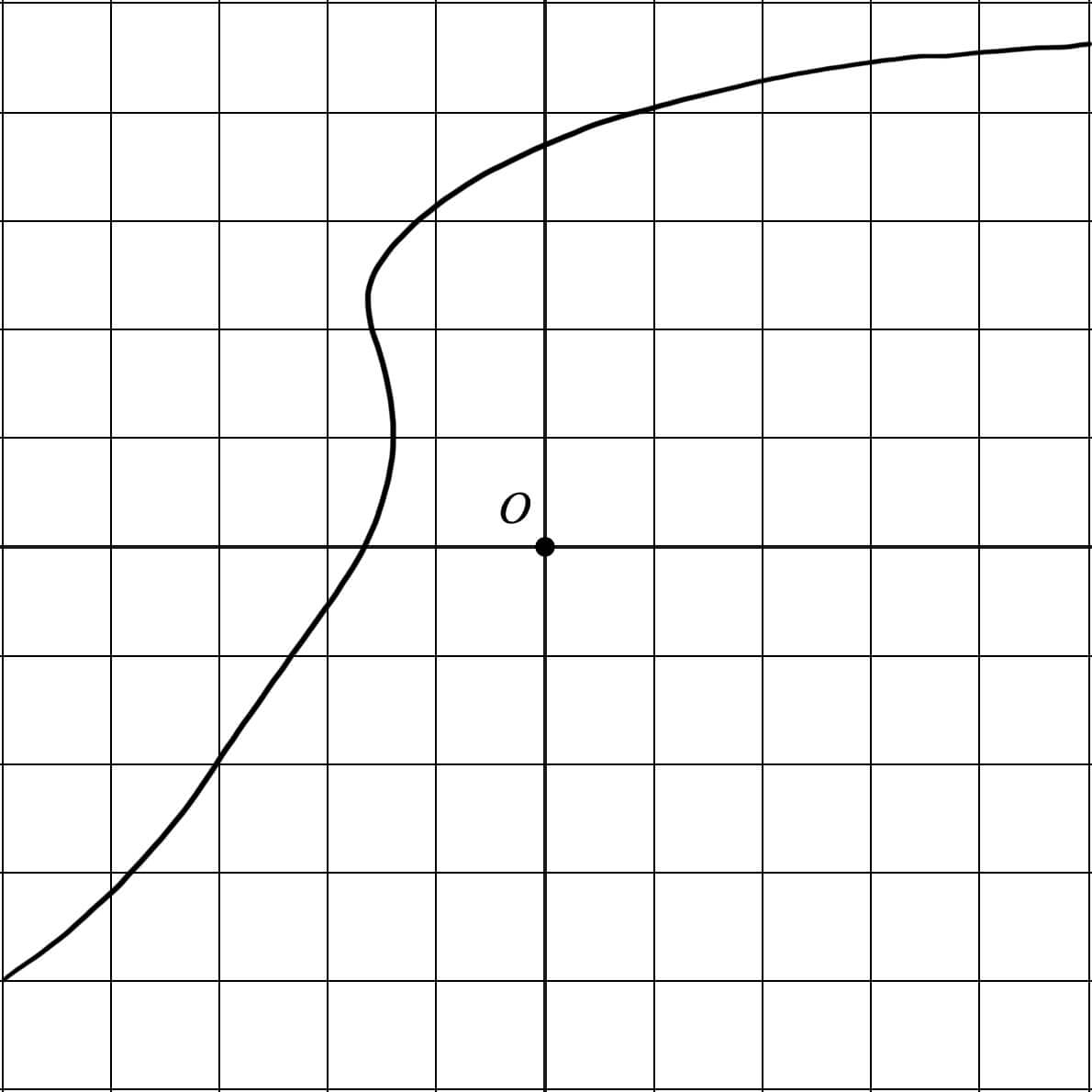
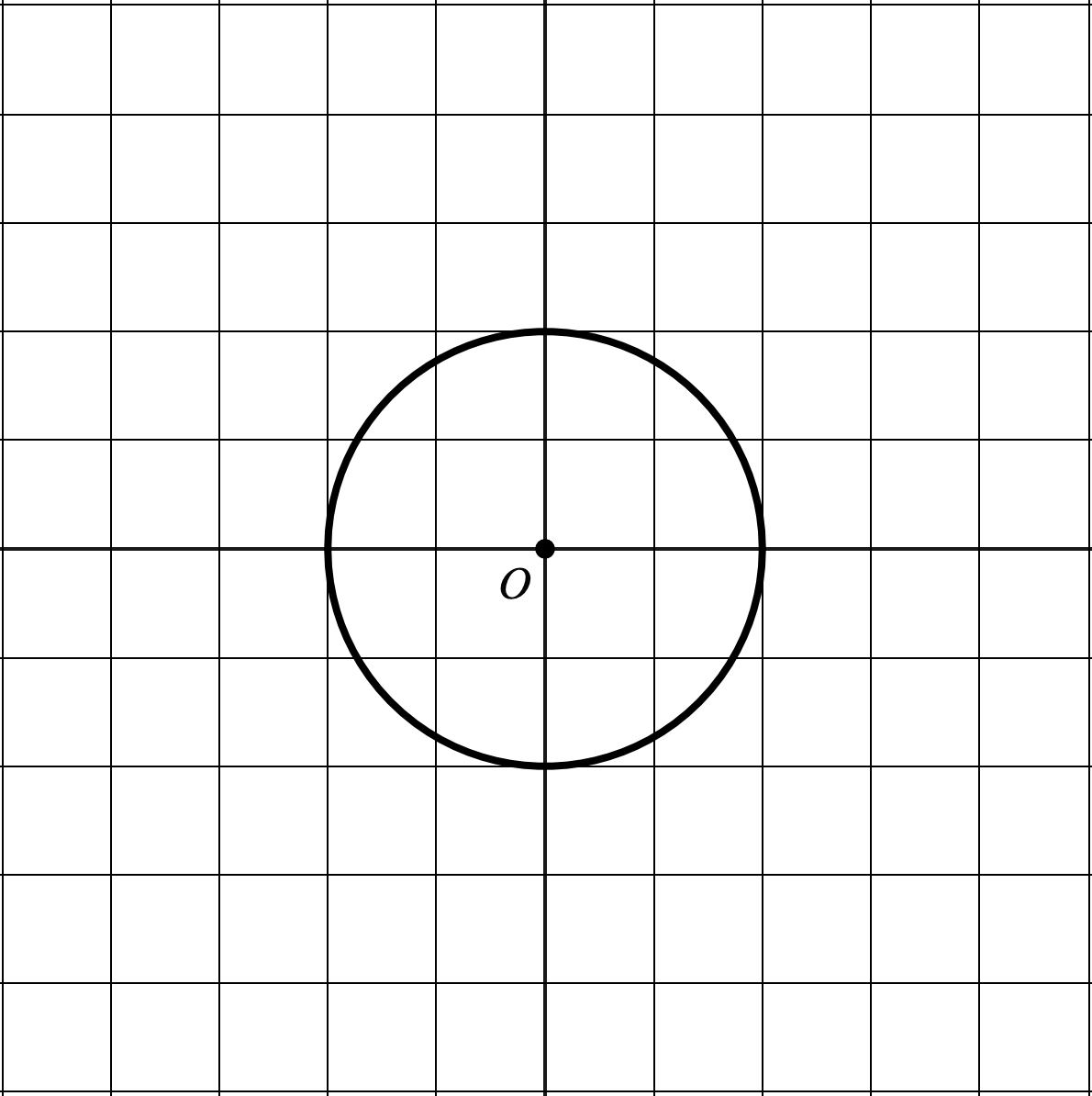
Déterminer si les courbes suivantes peuvent représenter des fonctions.

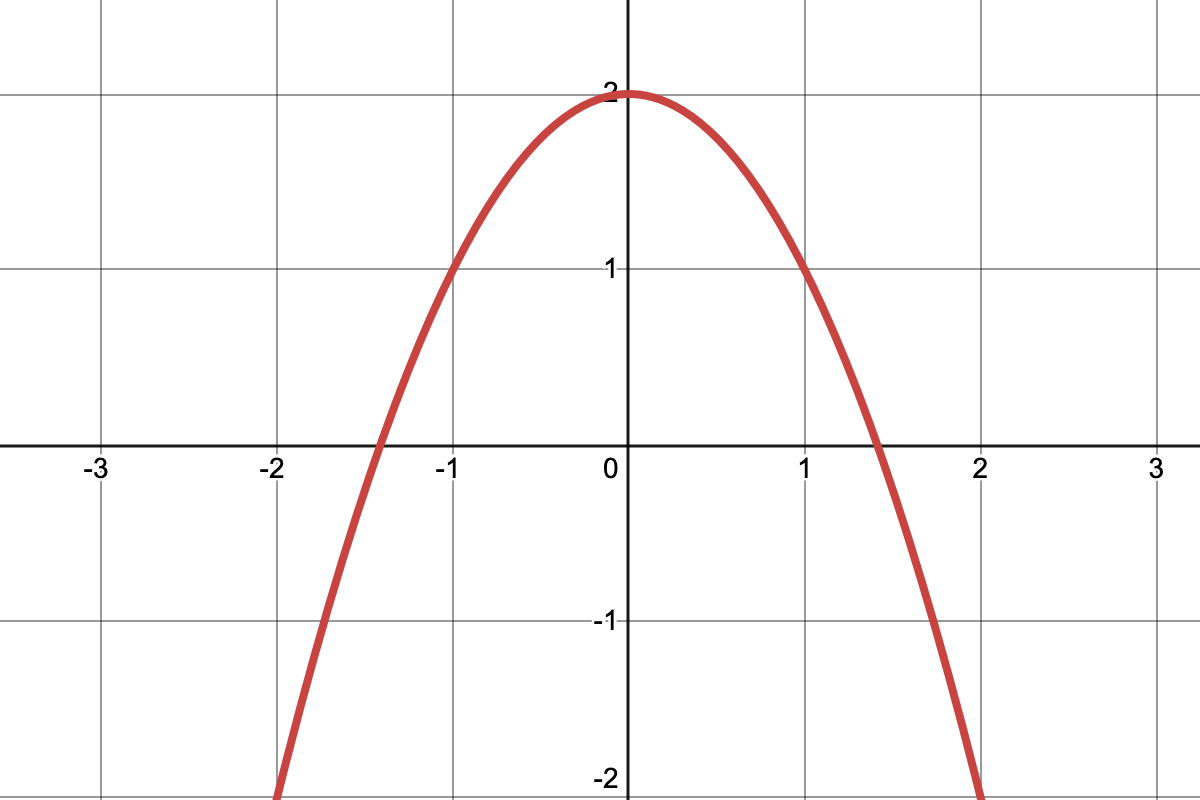
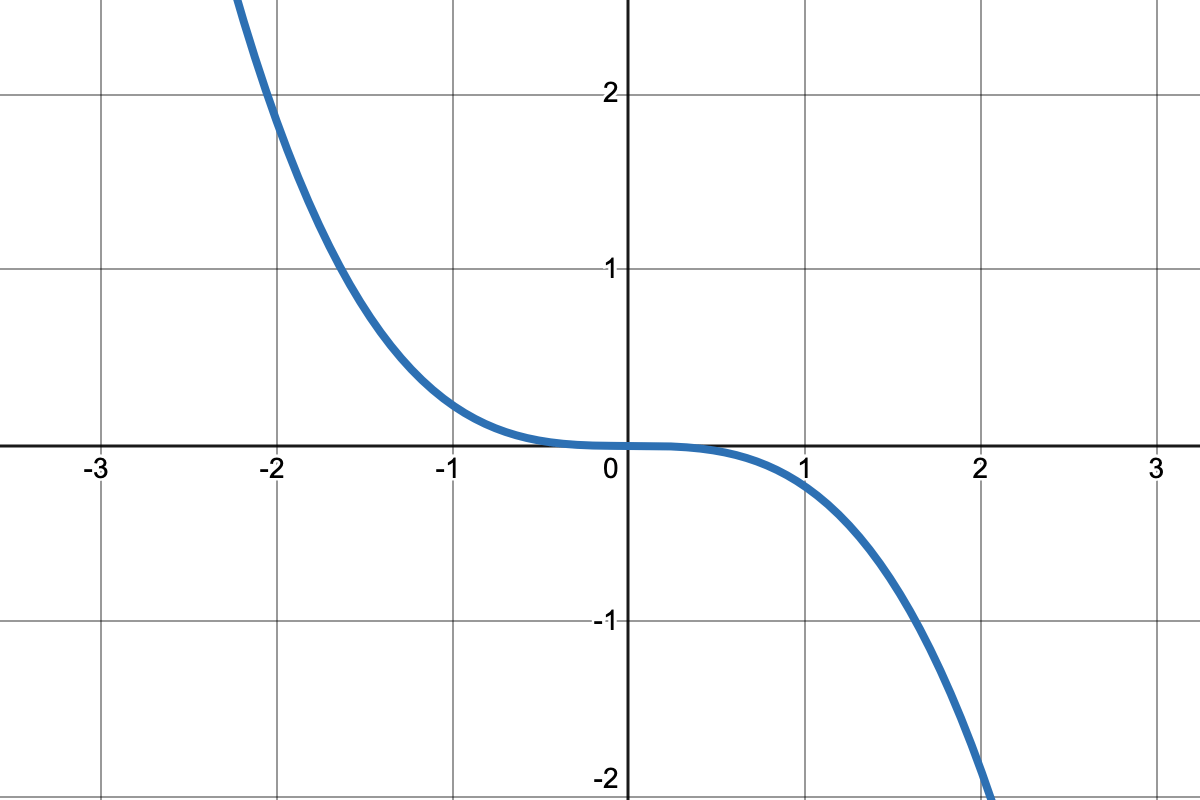
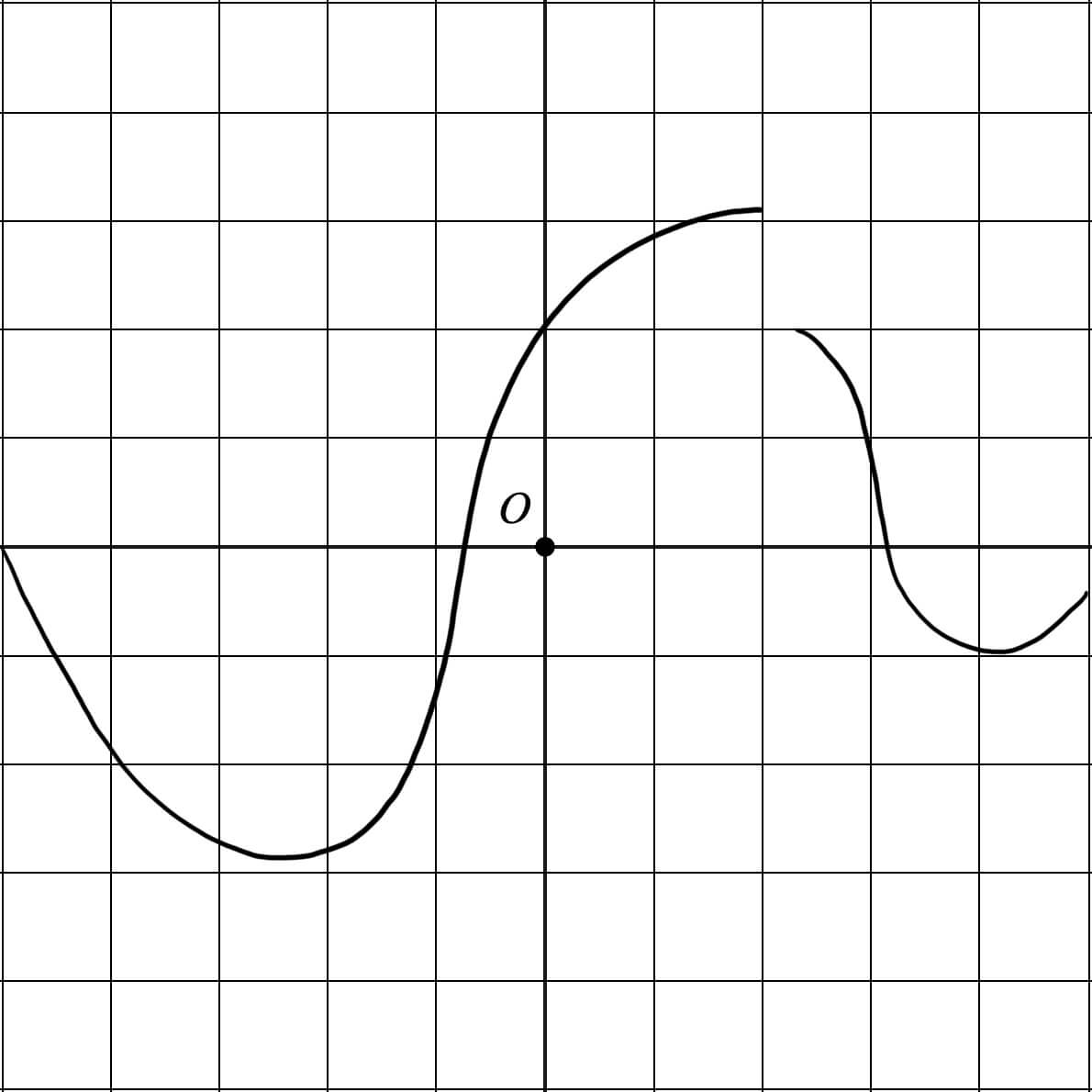
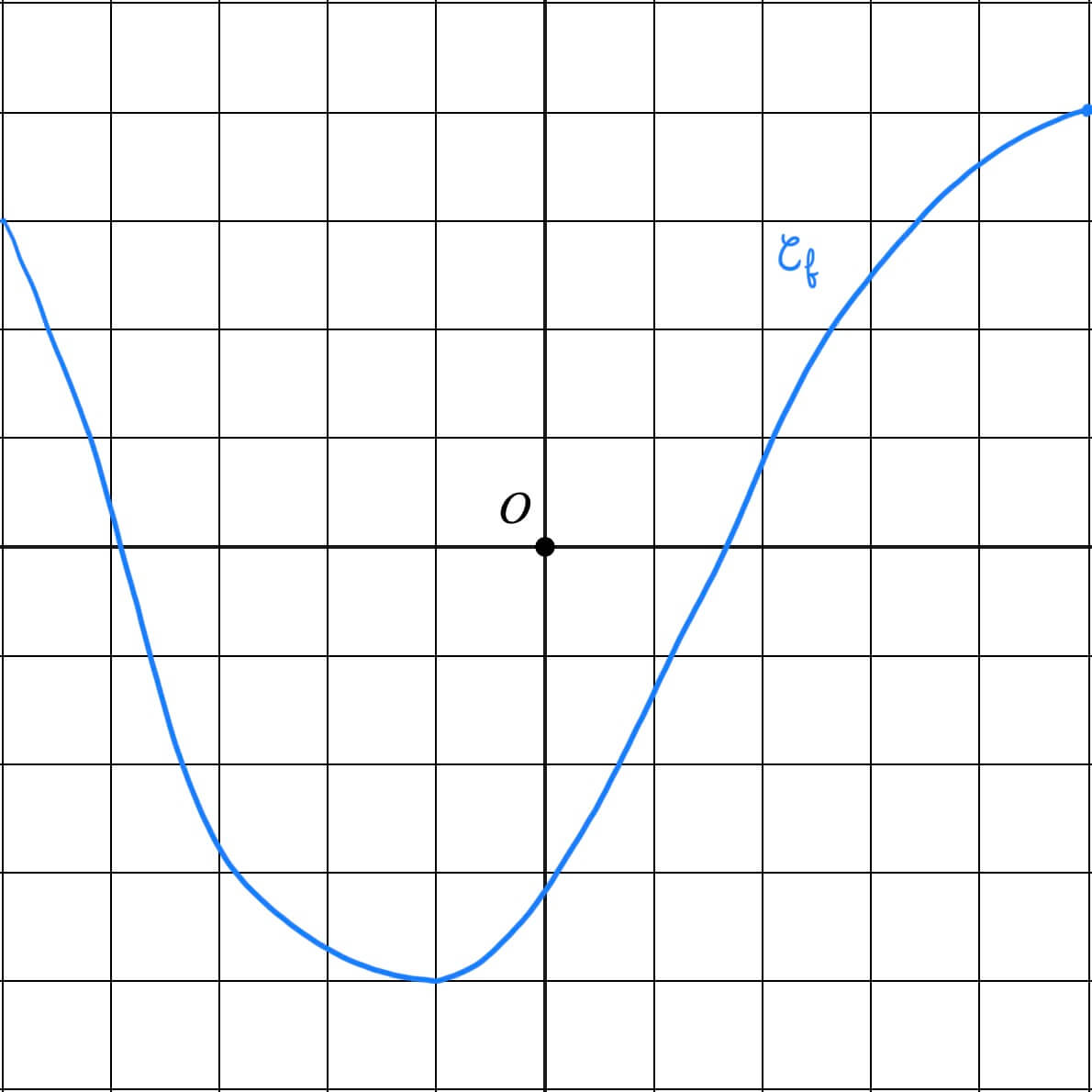
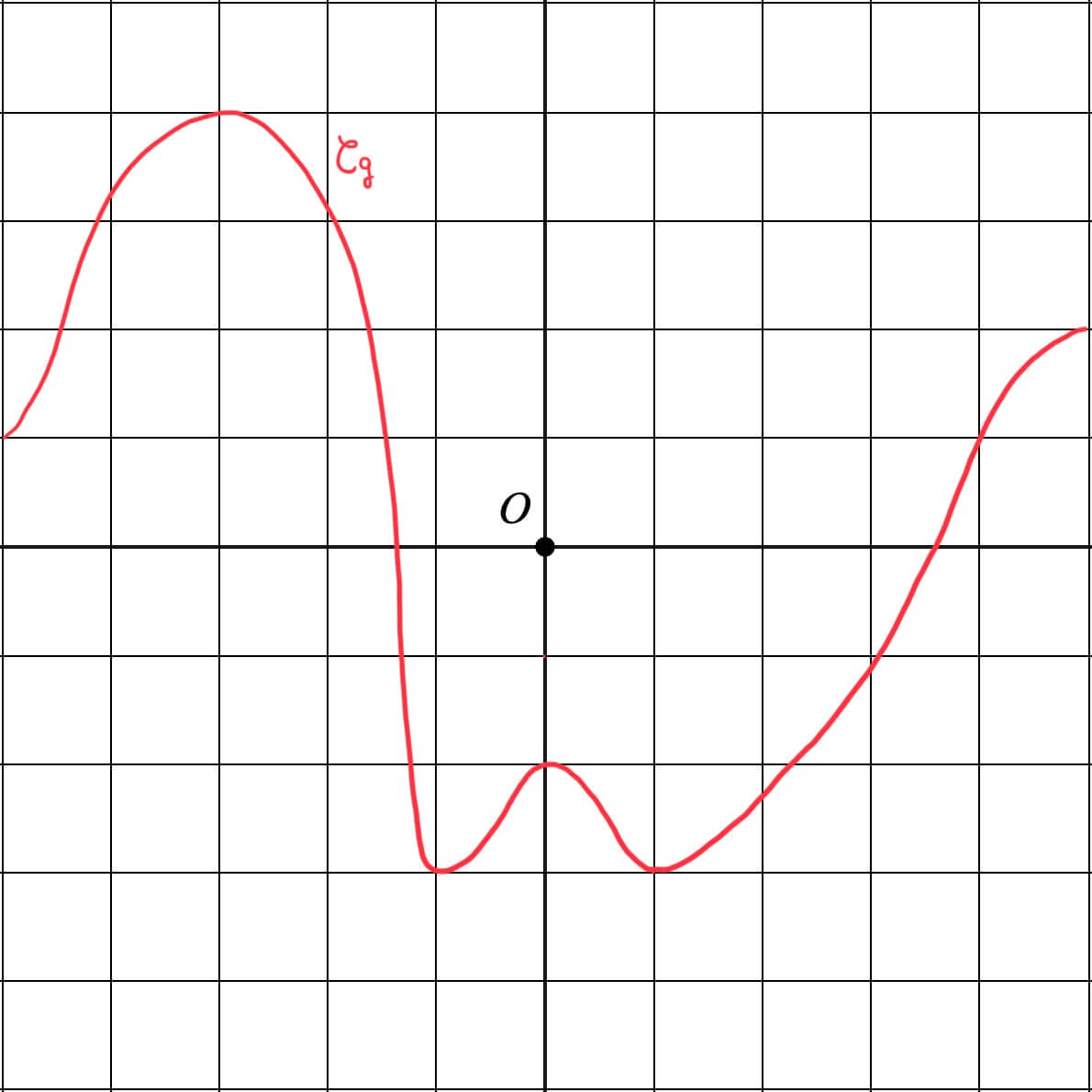
On considère les courbes de $f$ et $g$ suivantes.

1. Déterminer le nombre de solutions de l'équation $f(x)=-2$ et $f(x)=4$
2. Déterminer le nombre de solutions de l'équation $g(x)=-2,5$ et $g(x)=3$
3. Déterminer l'intervalle auquel appartient le nombre réel $m$ tel que $f(x)=m$ admette exactement 2 solutions.
4. Déterminer l'intervalle auquel appartient le nombre réel $m$ tel que $g(x)=m$ admette exactement 3 solutions.

Résoudre l'équation $f(x)=g(x)$ dans les cas suivants et interpréter graphiquement.

1. $f(x)=4x-1$ et $g(x)=7$
2. $f(x)=-2x+5$ et $g(x)=4x-3$
3. $f(x)=x^3$ et $g(x)=x^2$
4. $f(x)=\dfrac{3}{x-1}$ et $g(x)=\dfrac{1}{3x-2}$
5. $f(x)=x-2x^2$ et $g(x)=x^3+2x$
6. $f(x)=x^4$ et $g(x)=1$