Soit $E=\{-1;3;5\}$

1. Déterminer $card(E^2)$ et $E^2$
2. Combien de 5-uplets d'éléments de $E$ peut-on former?
3. Dans chaque cas donner 1 élément appartenant aux ensembles suivants:
$\N^3$ $\R \times \Z$ $\R^2$ $\Z \times \mathbb{Q}^2$

Déterminer le nombre d'anagrammes (mêmes lettres mais dans un ordre différent) que l'on peut former pour chacun des mots suivants, en utilisant le nombre de permutations $n!$

1. OVALE
2. EQUIPE
3. COOPERATION
4. ANANAS

Dénombrer dans les cas suivants:

1. Compter le nombre d'anagrammes des mots: POULPE, ANAGRAMME, LITTERATURE
2. Combien de mots de 8 lettres peut-on former avec les lettres A et B?
3. Combien de mots de 8 lettres peut-on former avec exactement 5 lettres A et 3 lettres B?
4. Combien de mots à 10 lettres peut-on former avec les lettres A, B, C et D?
5. Combien de mots de 10 lettres peut-on former avec exactement 4 lettres A, 3 lettres B et 3 lettres C?

Le but de cet exercice est de démontrer la relation de Pascal: si $1\leq k \leq n-1$ alors $\dbinom{n}{k}=\dbinom{n-1}{k-1}+\dbinom{n-1}{k}$

Méthode 1: On considère un ensemble $E$ de $n$ éléments et on note un de ces éléments $A$.

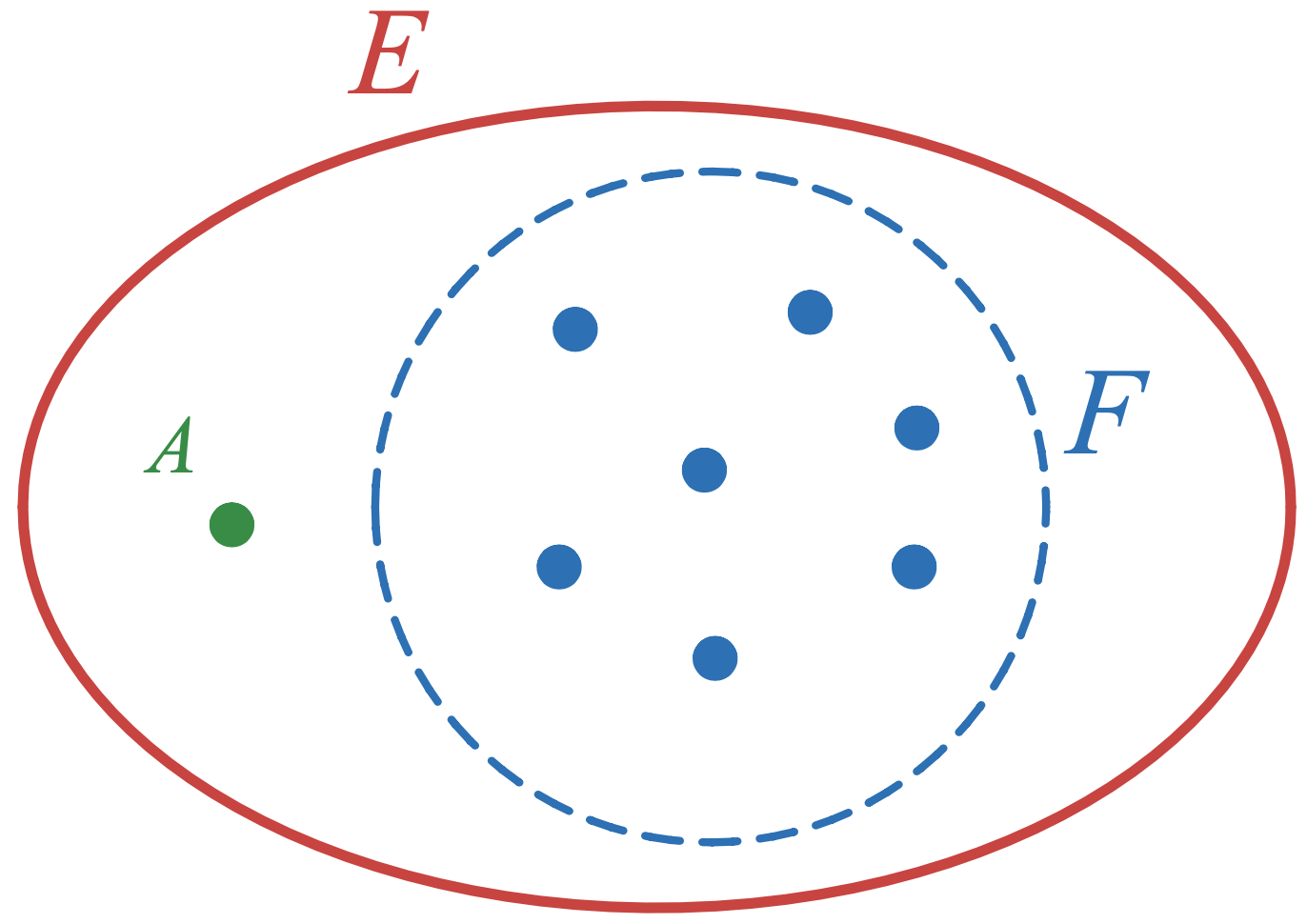
1. De combien de façons peut-on choisir $k$ éléments parmi les éléments de $F$?
2. De combien de façons peut-on choisir $k-1$ éléments parmi les éléments de $F$?
3. Conclure

Méthode 2: Par le calcul, en utilisant la formule $\dbinom{n}{k}=\dfrac{n!}{k!(n-k)!}$

1. Montrer que pour tout entier $n$:
$\dbinom{n}{0}=1$ $\dbinom{n}{1}=n$ $\dbinom{n}{2}=\dfrac{n(n-1)}{2}$
2. En déduire les valeurs de:
$\dbinom{n}{n}$ $\dbinom{n}{n-1}$ $\dbinom{n}{n-2}$
3. Déterminer sans calculatrice les valeurs de:
   1. $\dbinom{10}{2}-\dbinom{6}{1}+\dbinom{8}{7}+\dbinom{11}{9}-\dbinom{4}{4}$
   2. $\dbinom{5}{0}+\dbinom{5}{1}-\dbinom{5}{2}+\dbinom{5}{3}-\dbinom{5}{4}+\dbinom{5}{5}$

On considère l'algorithme Python suivant:

1. Décrire ce que calcule cet algorithme
2. Quelle est la valeur de f(3,7)?
3. Écrire un algorithme qui permet de calculer $n!$ quelle que soit la valeur de l'entier $n$