On souhaite aller du point A au point B dans le quadrillage ci-dessous en utilisant seulement des mouvements vers le haut et à droite sur chaque arête.

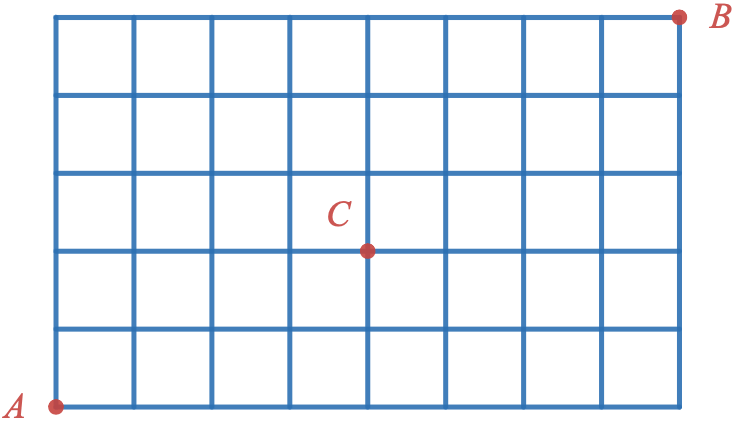
1. Combien de chemin différents vont de A à B?
2. Combien de chemin différents vont de A à B en passant par le point C?

On considère $N$ points du plan avec $N \geq 2$.

1. Combien de segments peut-on tracer entre ces $N$ points distincts du plan?
2. Combien de triangles et quadrilatères peut-on former avec ces $N$ points?
3. En déduire le nombre de polygones à $p$ côtés (avec $p \leq N$) que l'on peut former avec ces $N$ points.
4. Calculer le nombre d'hexagones que l'on peut former à partir de 8 points distincts.

On considère désormais un polygone à $p$ côtés (avec $p \leq N$). On aimerait dénombrer le nombre de diagonales que l'on peut former.

5. Méthode 1 Compter le nombre segments que l'on peut former à partir des $p$ points, sans oublier que certains sont des côtés du polygone et non des diagonales. En déduire le nombre de diagonales.
6. Méthode 2 Pour former une diagonale, on commence par choisir un point du polygone, puis il faut choisir les points que l'on peut relier au point initialement choisi. En déduire le resultat souhaité.

Une urne contient 15 boules numérotées de 1 à 15. On effectue au hasard et avec remise 5 tirages successifs d’une boule, et on note les numéros obtenus dans l’ordre d’apparition.

1. Combien de résultats différents peut-on obtenir?
2. Combien y a-t-il de résultats avec cinq numéros tous différents?
3. On note $A$ l'événement : « obtenir cinq numéros tous différents ». Définir par une phrase l'événement $\overline{D}$ puis calculer $P(A)$ et $P(\overline{A})$.

On s'intéresse maintenant aux anniversaires d'un groupe de personnes. Pour chaque personne, on considère que 365 jours sont possibles pour leur anniversaire.
On dispose d'une urne qui contient 365 boules numérotés de 1 à 365. Tirer au hasard un nombre parmi ces 365 revient à associer une date d'anniversaire à une personne.
Le fait que plusieurs personnes puissent avoir le même jour d'anniversaire correspond à tirer plusieurs fois le même nombre parmi les 365 possibles.

4. On effectue au hasard et avec remise 5 tirages successifs. Quelle est le nombre de résultats possibles?
5. En s'inspirant de la première partie, déterminer la probabilités d'avoir au moins deux numéros identiques.
6. Quelle est donc la probabilité que parmi 5 personnes, au moins deux aient le même anniversaire? Faire le même calcul pour 10, 15 et 20 personnes.
7. Compléter le programme suivant qui calcule la probabilité d'avoir au moins deux personnes qui ont le même anniversaire dans un groupe de $n$ personnes.