Basique

Intermédiaire

Section active

Avancé

Les exercices

sur 6 exercices complétés

Gratuit
Exercice 1 - Transformer un programme de calcul sous forme d'expression littérale
NO VIDEO

Utiliser la variable $x$ pour exprimer chacun des programmes de calcul suivants

  1. Choisir un nombre
    Ajouter 3
    Multiplier par -2
    Ajouter 3 fois le nombre initial
Gratuit
Exercice 2 - Factoriser grâce aux identités remarquables
NO VIDEO

Factoriser les expressions suivantes.

  1. $A=x^2-25$
  2. $B=4x^2-49$
  3. $C=100-36x^2$
  4. $D=\dfrac{4}{9}x^2-\dfrac{49}{81}$
Gratuit
Exercice 3 - Développer et réduire des identités remarquables plus complexes
NO VIDEO

Développer et réduire les expressions suivantes.

  1. $A=(-5x+11)^2$
  2. $B=(7x-4)^2$
  3. $C=(-3x-8)^2$
  4. $D=(\dfrac{4}{3}x-5)^2$
  5. $E=(\dfrac{5}{7}x+\dfrac{7}{2})^2$
Gratuit
Exercice 4 - Factoriser en utilisant une identité remarquable - 2
NO VIDEO

Factoriser les expressions suivantes.

  1. $A=x^2+2x+1$
  2. $B=x^2-6x+9$
  3. $C=x^2+10x+25$
  4. $D=4x^2-24x+9$
  5. $D=\dfrac{4}{9}x^2+8x+36$
Gratuit
Exercice 5 - Utiliser les expressions littérales pour calculer un volume
NO VIDEO
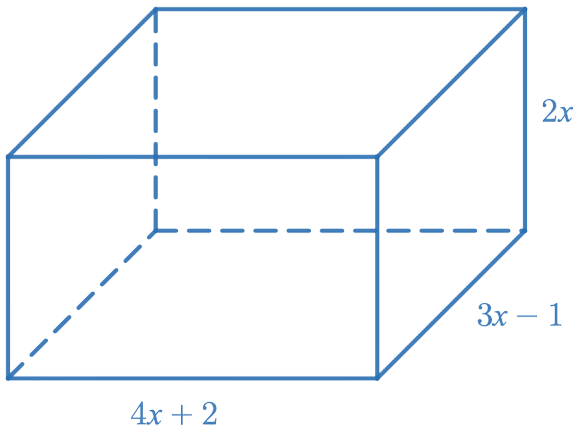
  1. Exprimer l'aire de ce pavé en fonction de $x$
  2. Exprimer le volume de ce pavé en fonction de $x$
  3. Calculer l'aire et le volume lorsque $x=4$
Gratuit
Exercice 6 - Développer, factoriser et utiliser la bonne expression
NO VIDEO

Soit $A=x^2-5x+4$.

  1. Montrer que $A=(x-1)(x-4)$
  2. Montrer que $A=(x-\dfrac{5}{2})^2-\dfrac{9}{4}$
  3. Utiliser l'expression la plus adaptée de $A$ lorsque $x=0$, $x=4$ et $x=\dfrac{5}{2}$