Les exercices
sur 5 exercices complétés
Exercice 1
- Lecture graphique de coordonnées
NO VIDEO
Déterminer les coordonnées des points dans le repère
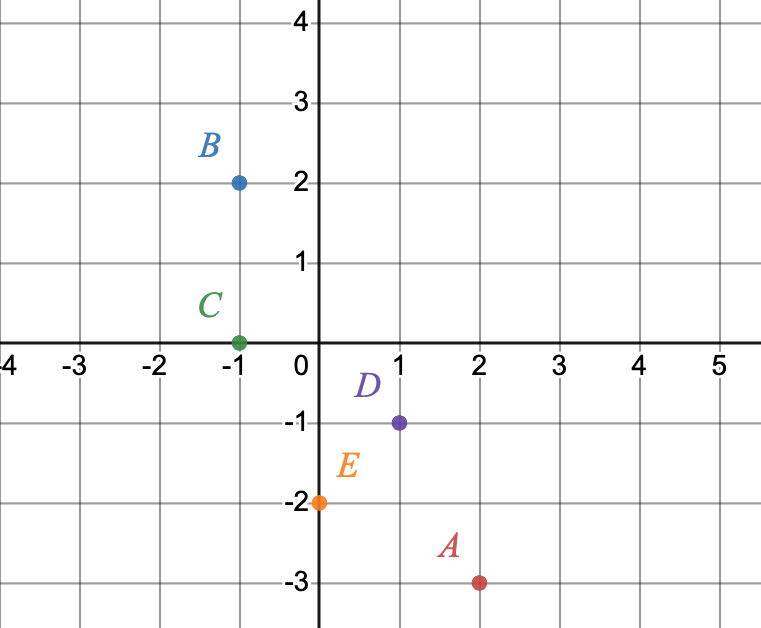
Exercice 2
- Coordonnées du milieu d'un segment
NO VIDEO
On considère les points $A(1;-1)$, $B(4;0)$, $C(5;-5)$, $D(2;-6)$
- Déterminer les coordonnées du point $M$ milieu de $[AB]$ et du point $N$ milieu de $[CD]$
- Déterminer les coordonnées du point $J$ milieu de $[AC]$ et du point $K$ milieu de $[BD]$
- Que peut-on en déduire sur le quadrilatère $ABCD$
Exercice 3
- Coordonnées du symétrique d'un point
NO VIDEO
On considère les points $A(4;-3)$, $B(-5;2)$, $C(-8;-4)$, $D(9;5)$
- Justifier pourquoi le point $E(-14;7)$ est le symétrique de $A$ par rapport à $B$.
- Déterminer les coordonnées du point $M$ symétrique de $C$ par rapport à $B$
- $F$ est le point du plan tel que $[AC]$ et $[BF]$ ont le même milieu. Déterminer les coordonnées de $F$
Exercice 4
- Distance entre 2 points
NO VIDEO
On considère les points $A(-2;1)$, $B(4;-3)$, $C(-1;-4)$
- Placer les points dans un repère et conjecturer la nature du triangle $ABC$
- Calculer les longueurs $AB$, $AC$ et $BC$
- En déduire la nature du triangle $ABC$
Exercice 5
- Vrai-faux repérage du plan
NO VIDEO
Indiquer si chaque affirmation est vraie ou fausse
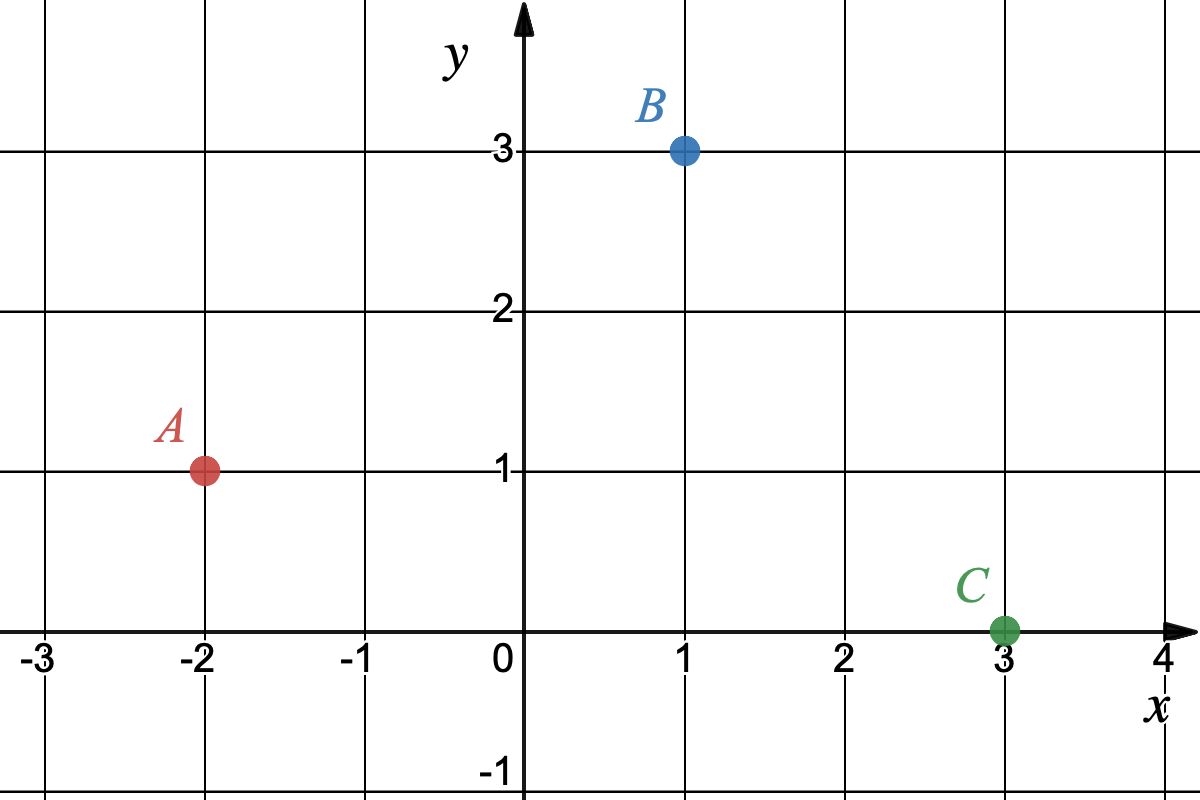
- Les coordoonnées de $A$ sont $(1;-2)$
- Les coordoonnées du milieu de $[AB]$ sont $(-\frac{1}{2};2)$
- $BC=\sqrt{13}$
- $ABC$ est isocèle en $B$
- $ABC$ est rectangle en $B$
- Soit $D(0;-2)$, $ABCD$ est un parallélogramme
Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire
Repérage et configurations planes
Fiche de synthèse
Contenu Complet Premium
Pour accéder au contenu complet de cette fiche de cours, vous devez vous abonner à notre offre premium.
Avec l'abonnement premium :
- Fiches de cours complètes
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Vidéos explicatives détaillées


