Les exercices
Exercice 1 - Droites de l'espace et orthogonalité
On considère les droites $d$ et $d'$ de représentations paramétriques:
$$d: \begin{cases}x=-t+2\\ y=2t+1\\ z=5t-4\end{cases}$$
$$d': \begin{cases}x=3t-2\\ y=-t+2\\ z=t\end{cases}$$
- Les droites sont-elles orthogonales?
- Les droites sont-elles perpendiculaires?
Exercice 2 - Orthogonalité dans un cube
On considère le cube ABCDEFGH ci-dessous.
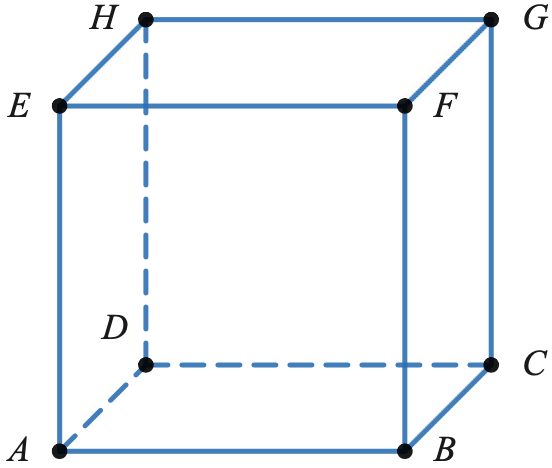
- Justifier que $(EF)$ est orthogonale au plan $(FGC)$, puis que $(EF)$ et $GC$ sont orthogonales.
- Justifier que les droites $(BC)$ et $(EG)$ ne sont pas orthogonales.
- $(AH)$ et $(BH)$ sont-elles orthogonales?
Exercice 3 - Produit scalaire dans l'espace et mesure d'angle
Soit les points $A(-1;3;2)$, $B(2;-5;0)$ et $C(-4;11;3)$
- Calculer le produit scalaire $\overrightarrow{AB}.\overrightarrow{AC}$
- Calculer $AB$ et $AC$.
- En déduire la mesure de l'angle $\widehat{BAC}$.
Exercice 4 - Équations de plans, vecteur normal et point dans le plan
Pour chacun des plans suivants donner un vecteur normal et vérifier si le point donné est dans le plan.
- $x-2y+3z+2=0$ et $A(-1; 3; \frac{5}{3})$
- $4x-3z+1=0$ et $B(0; 5; -1)$
- $\frac{x}{2}+y-6z+5=0$ et $C(6; -5; \frac{1}{2})$
- $\sqrt{2}x+2\sqrt{3}y+4=0$ et $D(\sqrt{2}; -\sqrt{3}; \sqrt{5})$
Exercice 5 - Équations de droites et plans dans l'espace et intersection
On considère la droite $(d)$ de représentation paramétrique:
$$d: \begin{cases}x=-2t+5\\ y=t+2\\ z=3t-4\end{cases}$$
et le point $A(-2; 4; 1)$
- Déterminer une équation du plan orthogonal à $(d)$ et passant par $A$.
- Déterminer les coordonnées du point d'intersection entre la droite et le plan.
Exercice 6 - Produit scalaire dans un cube et droites orthogonales
On considère le cube ABCDEFGH d'arête 4 ci-dessous.
- Montrer que les droites $(BG)$ et $(EC)$ sont orthogonales.
- Calculer les produits scalaires $\overrightarrow{AB}.\overrightarrow{AD}$ et $\overrightarrow{CA}.\overrightarrow{CF}$
