L'espace est muni d'un repère orthonormé $(O, \vec{i}, \vec{j}, \vec{k})$. On considère les points $A(-1;2;1)$, $B(1;-6;-1)$ et $C(2;2;2)$

1. Vérifier que les points $A$, $B$ et $C$ définissent un plan.
2. Montrer que le vecteur $\vec{n} \begin{pmatrix} 1 \\1 \\ -3 \end{pmatrix}$ est un vecteur normal au plan $(ABC)$.
3. Déterminer une équation cartésienne du plan $(ABC)$.

Soit $P$ le plan d'équation: $x-y+z-4=0$

4. Montrer que les plans $(ABC)$ et $P$ sont sécants.
5. Soit $D$ la droite d'intersection des plans $P$ et $(ABC)$. Déterminer une représentation paramétrique de la droite $D$.

On considère le cube ABCDEFGH d'arête 1 ci-dessous. Dans tout l'exercice l'espace est rapporté au repère orhonormé $(D; \overrightarrow{DA}; \overrightarrow{DC}; \overrightarrow{DH})$.

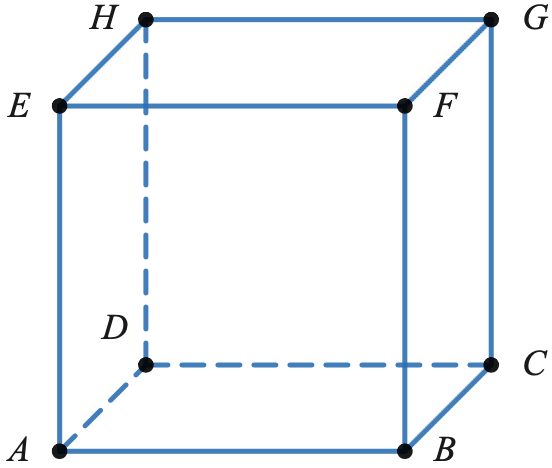
1. Soit $K$ le point tel que $\overrightarrow{KD}+2\overrightarrow{KF}=\vec{0}$. Montrer que les coordonnées de $K$ sont $(\dfrac{2}{3}~;~\dfrac{2}{3};\dfrac{2}{3})$.
2. Montrer que les droites $(EK)$ et $(DF)$ sont orthogonales.
3. Calculer la distance $EK$.

Soit $M$ un point du segment $[HG]$. On note $m=HM$ avec $m\in [0;1]$.

4. Montrer qu'une équation cartésienne du plan $(MFD)$. est $(-1+m)x+y-mz=0$.
5. Montrer que pour tout réel $m\in [0;1]$ la distance $d_m$ du point $E$ au plan $(MFD)$ est donnée par: $$d_m = \dfrac{1}{\sqrt{2m^2-2m+2}}$$
6. Déterminer la position de $M$ pour laquelle la distance $d_m$ est maximale.
7. Montrer que la distance maximale vaut $d_{m}=d(E; (MFD)) = \dfrac{\sqrt{6}}{3} = EK$.
8. Après avoir rappelé pourquoi le point $K$ appartient à la droite $(FD)$, montrer que lorsque la distance $d_m$ est maximale, $K$ est le projeté orthogonal de $E$ sur le plan $MFD$.

Dans un tétraèdre, le segment joignant un sommet au centre de gravité de la face opposée est appelée médiane. Ainsi, le segment $[AA']$ est une médiane du tétraèdre $ABCD$ ci-dessous.

PARTIE A

$ABCD$ est un tétraèdre régulier, c'est-à-dire un solide dont les quatre faces sont des triangles équilatéraux. $A'$ est le centre de gravité du triangle $BCD$, c'est à dire le point d'intersection des médianes issues des sommets $B$, $C$, $D$.

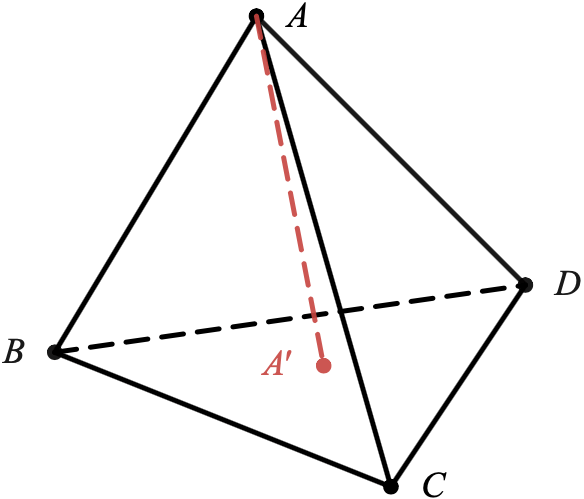
1. En utilisant le point $I$, milieu de $[BD]$, montrer que $\overrightarrow{AA'}.\overrightarrow{BD}=0$
2. En utilisant le point $J$, milieu de $[BC]$, montrer que $\overrightarrow{AA'}.\overrightarrow{BC}=0$
3. En déduire que la droite $(AA')$ est perpendiculaire au plan $(BCD)$.

On a prouvé la propriété selon laquelle dans un tétraèdre régulier la médiane issue d'un sommet est orthogonale à la face opposée.

PARTIE B

On munit l'espace d'un repère orthonormal $(O,~\vec{i},~\vec{j},~\vec{k})$. On considère les points $P(1~;~2~;~3)$, $Q(4~;~2~;~- 1)$ et $R(-2~;~3~;~0)$.

1. Montrer que le tétraèdre $OPQR$ n'est pas régulier.
2. On rappelle que le centrer de gravité $G$ d'un triangle $ABC$ quelconque vérifie la relation vectorielle: $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$. Calculer les coordonnées de $P'$, centre de gravité du triangle $OQR$.
3. Vérifier qu'une équation cartésienne du plan $(OQR)$ est: $3x+2y+16z=0.$
4. La propriété de la partie A est-elle vérifiée?