Fonctions logarithmes

Basique

Intermédiaire

Avancé

Contrôles d'entraînement

Contrôle d'entraînement logarithmes n˚1

Exercice 1D'après Bac Amerique du Nord 2018

Lors d'une expérience en laboratoire, on lance un projectile dans un milieu fluide. L'objectif est de déterminer pour quel angle de tir $\theta$ par rapport à l'horizontale la hauteur du projectile ne dépasse pas $1,6$ mètre.
Comme le projectile ne se déplace pas dans l'air mais dans un fluide, le modèle parabolique usuel n'est pas adopté.
On modélise ici le projectile par un point qui se déplace, dans un plan vertical, sur la courbe représentative de la fonction $f$ définie sur l'intervalle $[0~;~1[$ par: $$f(x) = bx + 2ln (1- x)$$ où $b$ est un paramètre réel supérieur ou égal à $2$, $x$ est l'abscisse du projectile, $f(x)$ son ordonnée, toutes les deux exprimées en mètres.

  1. La fonction $f$ est dérivable sur l'intervalle $[0~;~1[$. On note $f'$ sa fonction dérivée.
    On admet que la fonction $f$ possède un maximum sur l'intervalle $[0~;~1[$ et que, pour tout réel $x$ de l'intervalle $[0~;~1[$: $$f'(x) = \dfrac{- bx + b - 2}{1 - x}$$ Montrer que le maximum de la fonction $f$ est égal à $b - 2 + 2ln \left(\dfrac{2}{b}\right)$.
  2. Déterminer pour quelles valeurs du paramètre $b$ la hauteur maximale du projectile ne dépasse pas $1,6$ mètre.
  3. Dans cette question, on choisit $b = 5,69$.
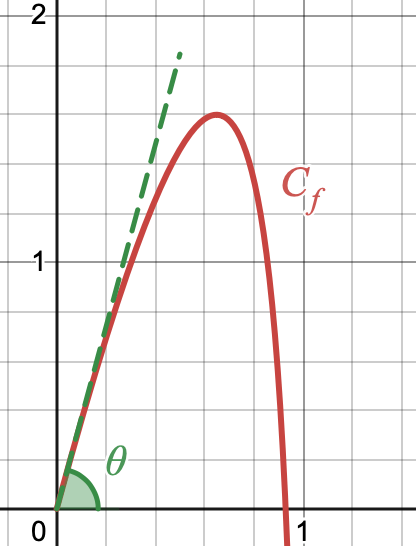
    L'angle de tir $\theta$ correspond à l'angle entre l'axe des abscisses et la tangente à la courbe de la fonction $f$ au point d'abscisse $0$ comme indiqué sur le schéma donné ci-dessus.
    Déterminer une valeur approchée au dixième de degré près de l'angle $\theta$.
Exercice 2D'après Bac Antilles Guyane Maroc 2023

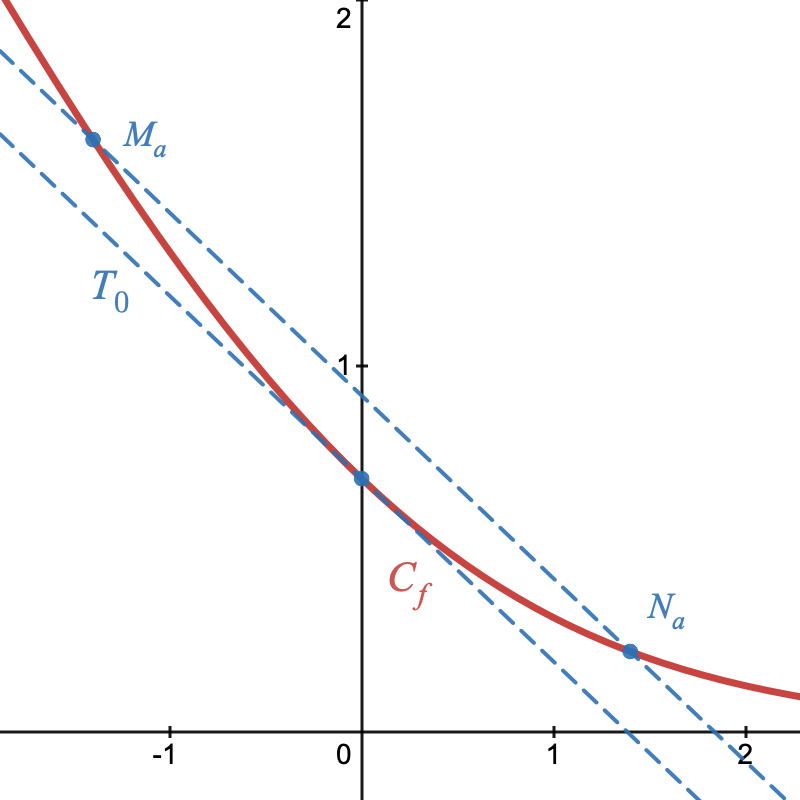
On considère la fonction $f$ définie sur $\R$ par:$$f(x)=ln(1+e^{-x})$$ On note $C_f$ sa courbe représentative dans un repère orthonormé $(O;~\vec{i};~\vec{j};~\vec{k})$.

La courbe $C_f$ est tracée ci-contre.

$T_0$ est la tangente à la courbe au point d'abscisse $0$.

    1. Déterminer la limite de la fonction $f$ en $-\infin$.
    2. Déterminer la limite de la fonction $f$ en $+\infin$. Interpréter graphiquement ce résultat.
    3. On admet que la fonction $f$ est dérivable sur $\R$ et on note $f'$ sa fonction dérivée.
      Calculer $f'(x)$ puis montrer que, pour tout nombre réel $x$, $f'(x)=\dfrac{-1}{1+e^x}$
    4. Dresser le tableau de variations complet de la fonction $f$ sur $\R$.
    1. Déterminer une équation de la tangente $T_0$.
    2. Montrer que la fonction est $f$ est convexe sur $\R$.
    3. En déduire que, pour tout nombre réel $x$, on a:$$f(x)\geq -\frac{1}{2}x+ln(2)$$
  3. Pour tout nombre réel $a$ différent de $0$, on note $M_a$ et $N_a$ les points de la courbe $C_f$ d'abscisses respectives $−a$ et $a$.
    On a donc: $M_a(-a;~f(-a))$ et $N_a(a;~f(a))$.
    1. Montrer que, pour tout nombre réel $x$, on a: $f(x)-f(-x)=-x$.
    2. En déduire que les droites $T_0$ et $(M_a N_a)$ sont parallèles.

Voir détail