On considère la fonction $g$ définie sur $]0;~+\infin[$ par $g(x)=ln(x)+1-\frac{1}{x}$.

1. Déterminer les limites de la fonction $g$ aux bornes de son ensemble de définition.
2. Étudier les variations de la fonction $g$ sur l'intervalle $]0;~+\infin[$
3. Calculer $g(1)$ et en déduire le signe de $g(x)$ sur $]0;~+\infin[$
4. Soit $f$ la fonction définie sur $]0;~+\infin[$ par $f(x)=xln(x)-ln(x)$. Montrer que pour tout $x\in ]0;~+\infin[$, $f'(x)=g(x)$
5. En déduire que $f$ est strictement croissante sur $]1;~+\infin[$.
6. Montrer que l'équation $f(x)=1-\frac{1}{e}$ admet une unique solution sur l'intervalle $]1;~+\infin[$, que l'on note $\alpha$.
7. Donner un encadrement de $\alpha$ d'amplitude $10^{-1}$.

On considère pour tout entier naturel $n>0$ les fonctions $f_n$ telles que $f_n(x)=\dfrac{ln(x)}{x^n}$ définies sur $]0;~+\infin[$

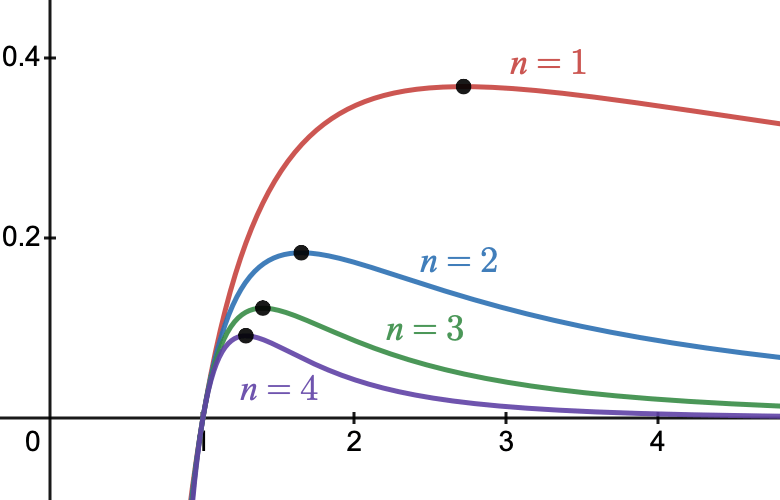
1. Montrer que pour tout entier naturel $n>0$, $f_{n}'(x)=\dfrac{1-nln(x)}{x^{n+1}}$
2. Dresser le tableau de variation de $f_n$ sur $]0;~+\infin[$
3. En notant $I_n$ le maximum de la fonction $f_n$ sur $]0;~+\infin[$, montrer que les coordonnées de $I_n$ a pour coordonnées $(e^{\frac{1}{n}};~\frac{1}{ne})$.
4. Montrer que les points $I_n$ appartiennent à la courbe d'équation $y=\dfrac{ln(x)}{e}$.

Soit $f$ une fonction définie et dérivable sur $\R$. On donne ci-dessous la courbe représentative de sa dérivée, $f'$.

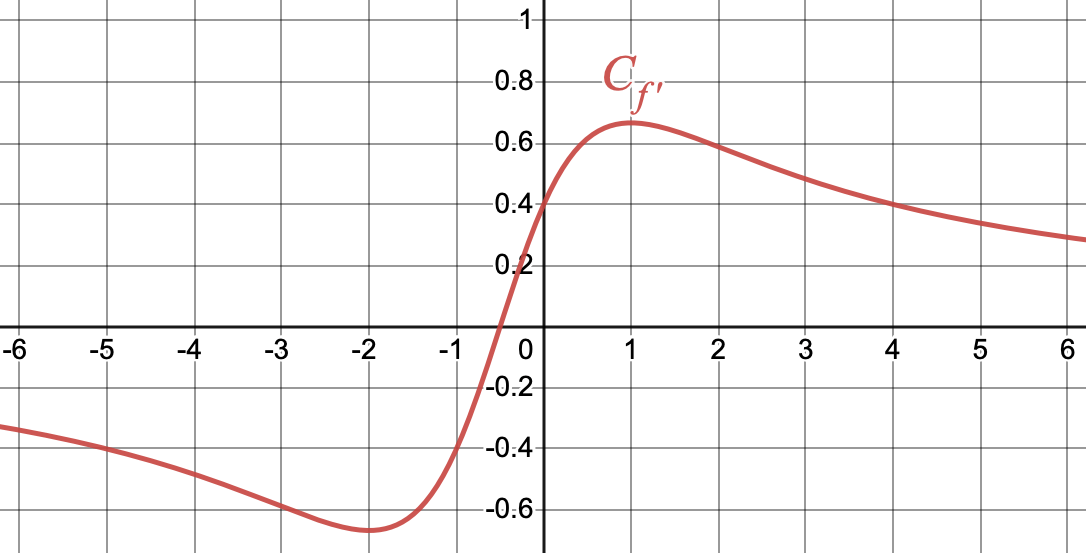
1. Déterminer graphiquement les variations de $f'$ sur $\R$ et en déduire la convexité de $f$ sur $\R$.
2. Dans la suite de l'exercice, la fonction $f$ est définie sur $\R$ par: $$f(x)=ln(x^2+x+\frac{5}{2})$$Justifier pourquoi la fonction est définie sur $\R$ et calculer les limites de $f$ en $+\infin$ et $-\infin$.
3. Déterminer une expression de $f'(x)$, la fonction dérivée de $f$, pour tout $x\in \R$.
4. En déduire le tableau de variations de $f$ sur $\R$.
5. Justifier que l'équation $f(x)=2$ admet une unique solution $\alpha$ dans l'intervalle $[-\frac{1}{2};~+\infin[$ et en donner une valeur approchée à $10^{-1}$ près.
6. Monter que pour tout $x\in \R$, $f''(x)=\dfrac{-2x^2-2x+4}{(x^2+x+\frac{5}{2})^2}$ et retrouver les résultats de la question 1.

On aimerait prouver le résultat suivant: $\lim\limits_{x \to +\infin }\dfrac{ln(x)}{x}=0$

Méthode 1

On rappelle que $\lim\limits_{x \to +\infin }\dfrac{e^x}{x}=+\infin$. Pour tout $x\in ]0;~+\infin[$, on pose $X=ln(x)$.

1. Démontrer que pour tout réel $x\in ]0;~+\infin[$, $\dfrac{ln(x)}{x}=\dfrac{X}{e^X}$.
2. En déduire que $\lim\limits_{x \to +\infin }\dfrac{ln(x)}{x}=0$.

Méthode 2

Soit $f$ la fonction définie sur $]0;~+\infin[$ par $f(x)=ln(x)-x+1$.

1. Étudier les variations de $f$ sur $]0;~+\infin[$ et en déduire que pour tout $x\in ]0;~+\infin[$:$$ln(x)\leq x-1$$
2. En déduire que pour tout $x\in ]0;~+\infin[$:$$\frac{1}{2}ln(x)\leq \sqrt{x}-1$$
3. Montrer que pour tout $x\in ]1;~+\infin[$, $$0<\frac{ln(x)}{x}\leq \frac{2(\sqrt{x}-1)}{x}$$
4. En déduire que $\lim\limits_{x \to +\infin }\dfrac{ln(x)}{x}=0$.