On considère la suite $\left(I_n\right)$ définie par $I_0 = \displaystyle\int_0^{\frac{1}{2}}\dfrac{1}{1 - x} \,dx$ et pour tout entier naturel $n$ non nul: $$I_n = \displaystyle \int_0^{\frac{1}{2}} \dfrac{x^n}{1-x} \,dx$$

1. Montrer que $I_0=ln(2)$.
2. 1. Calculer $I_0-I_1$.
   2. En déduire $I_1$.
3. 1. Montrer que pour tout entier naturel $n$:$$I_n-I_{n+1}=\dfrac{(\frac{1}{2})^{n+1}}{n+1}$$
   2. Proposer un algorithme permmettant de déterminer, pour un entier naturel $n$ donné, la valeur de $I_n$.
4. Soit $n$ un entier naturel non nul.
   On admet que si $x$ appartient à l'intervalle $\big[0;~\dfrac{1}{2}\big]$ alors $0\leq \dfrac{x^n}{1-x}\leq \dfrac{1}{2^{n-1}}$
   1. Montrer que pour tout entier naturel $n$ non nul:$$0\leq I_n \leq \dfrac{1}{2^n}$$.
   2. En déduire la limite de la suite $(I_n)$ lorsque $n$ tend vers $+\infin$.
5. Pour tout entier naturel $n$, on pose $$S_n=\dfrac{1}{2}+\dfrac{(\frac{1}{2})^2}{2}+\dfrac{(\frac{1}{2})^3}{3}+...+\dfrac{(\frac{1}{2})^n}{n}$$
   1. Montrer que pour tout entier naturel $n$ non nul, $S_n =I_0-I_n$.
   2. Déterminer la limite de $S_n$ lorsque $n$ tend vers $+\infin$.

On considère les fonction $f$ et $g$ de courbe $C_f$ et $C_g$ respectivees, définies par: $$f(x)=e^{-x}(-cos(x)+sin(x)+1)~~:~~g(x)=-e^{-x}cos(x)$$

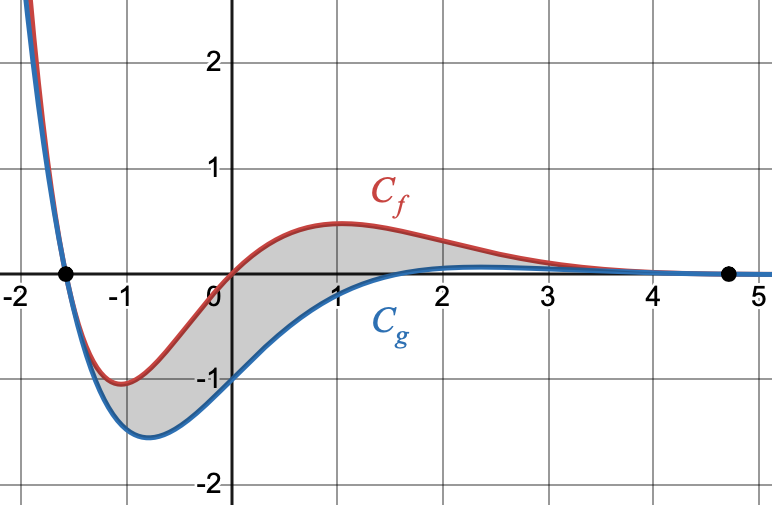
1. Étudier la position relative des courbe $C_f$ et $C_g$ sur $\R$.
2. On a représenté les courbes de $C_f$ et $C_g$ sur l'intervalle $[-2;~5]$. Démontrer que les points d'intersection de $C_f$ et $C_g$ dans l'intervalle $[-2;~5]$ sont les points de coordonnées $(-\dfrac{\pi}{2};~0)$ et $(\dfrac{3\pi}{2};~0)$.
3. Justifier que l'aire de la surface grisée vaut $\mathscr{A}=\displaystyle \int_{-\frac{\pi}{2}}^{\frac{3\pi}{2}} e^{-x}(sin(x)+1) \,dx$
4. Prouver que $0\leq \mathscr{A} \leq 2(e^{\frac{\pi}{2}}-e^{-\frac{3\pi}{2}})$
5. À l'aide d'une double intégration par parties déterminer $\mathscr{A}$ à $10^-2$ près.

On considère la fonction $h$ définie sur $\R$ par:$$h(x)=(x-1)e^{-2x}+1$$ On admet que la fonction $h$ est dérivable sur $\R$.
On note $C_h$ la courbe représentative de la fonction $h$ et $d$ la droite d'équation $y=x$.
La courbe $C_h$ et la droite $d$ sont représentées ci-dessous.
Soit $D$ le domaine du plan délimité par la courbe $C_h$, la droite $d$ et les droites d'équation $x=0$ et $x=1$.
Soit $A$ l'aire de $D$ exprimée en unité d'aire.

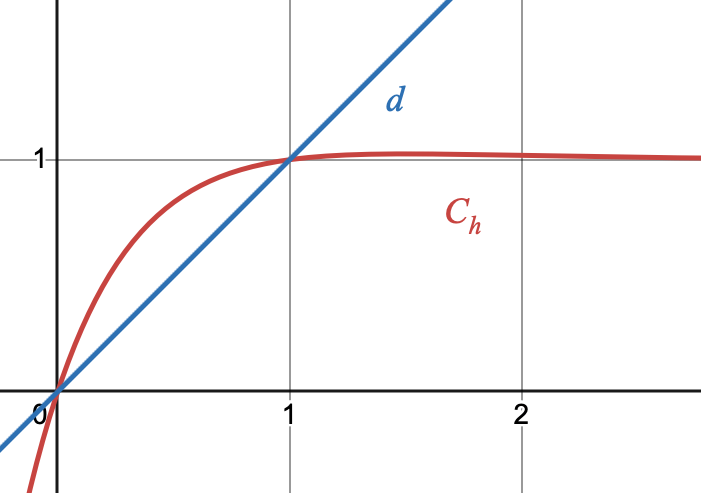
1. Hachurer le domaine $D$ et justifier que: $$A=\displaystyle \int_0^1 (h(x)-x) \,dx$$
2. 1. Démontrer que pour tout réel $x$,$$h(x)-x=(1-x)(1-e^{-2x})$$
   2. Soit $g$ la fonction définie sur $\R$ par $g(x)=e^{-2x}-1+2x$. Étudier les variations de $g$ sur $\R$.
   3. En déduire que pour tout $x\in \R$, $e^{-2x}\geq 1-2x$.
   4. Démontrer que pour tout réel $x$ de l'intervalle $[0;~1]$: $$h(x)-x\leq 2x-2x^2$$.
   5. En déduire que $A\leq \dfrac{1}{3}$.
3. 1. À l'aide d'une intégration par parties déterminer:$$\displaystyle \int_0^1 xe^{-2x} \,dx$$
   2. Utiliser le résultat précédent pour déterminer la valeur de $A$.

On considère, pour tout entier $n>0$, les fonctions $f_n$ définies sur l'intervalle $[1;~5]$ par: $$f_n(x)=\dfrac{ln(x)}{x^n}$$ Pour tout entier $n>0$, on note $C_n$ la courbe représentative de la fonction $f_n$ dans un repère orthogonal.
Sur le graphique ci-dessous sont représentées les courbes $C_n$ pour $n$ appartenant à ${1;~2;~3;~4}$.

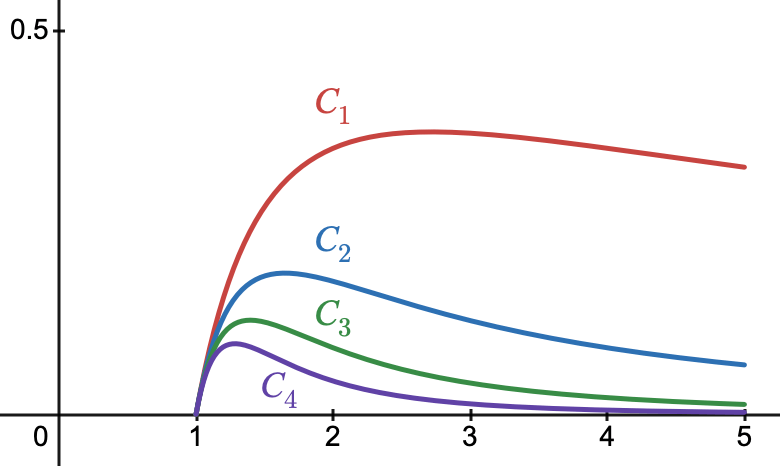
1. Montrer que pour tout entier $n>0$ et tout réel $x$ de l'intervalle $[1;~5]$: $$f_n'(x)=\dfrac{1-nln(x)}{x^{n+1}}$$
2. Pour tout entier $n > 0$, on admet que la fonction $f_n$ admet un maximum sur l'intervalle $[1;~5]$.
   On note $A_n$ le point de la courbe $C_n$ ayant pour ordonnée ce maximum.
   Montrer que tous les points $A_n$ appartiennent à une même courbe $\gamma$ d'équation: $$y=\dfrac{1}{e}ln(x)$$
3. 1. Montrer que, pour tout entier $n>1$ et tout réel $x$ de l'intervalle $[1;~5]$: $$0\leq \dfrac{ln(x)}{x^n} \leq \dfrac{ln(5)}{x^n}$$
   2. Montrer que pour tout entier $n>1$: $$\displaystyle \int_1^5 \dfrac{1}{x^n} \,dx=\dfrac{1}{n-1} \Big( 1-\dfrac{1}{5^{n-1}} \Big)$$
   3. Pour tout entier $n>0$, on s'intéresse à l'aire, exprimée en unités d'aire, de la surface sous la courbe $f_n$, c'est à dire l'aire du domaine du plan délimité par les droites d'équations $x=1$, $x=5$, $y=0$ et la courbe $C_n$.
      Déterminer la valeur limite de cette aire quand $n$ tend vers $+\infin$.