On considère les intégrales suivantes:$$I=\displaystyle \int_0^1 \dfrac{e^x}{e^x+1} \,dt~~;~~J=\displaystyle \int_0^1 \dfrac{1}{e^x+1} \,dt$$

1. Calculer $I$.
2. Prouver que $I+J=1$
3. En déduire la valeur de $J$.

Déterminer la valeur des intégrales suivantes à l'aide d'une intégration par parties.

1. $\displaystyle \int_{1}^2 xe^x \,dx$
2. $\displaystyle \int_{1}^e xln(x) \,dx$
3. $\displaystyle \int_{0}^3 \dfrac{x}{(x+4)^3} \,dx$
   
   On posera $u'(x)=\dfrac{1}{(x+4)^3}$ et $v(x)=x$
4. $\displaystyle \int_{-1}^1 x^3e^{x^2} \,dx$
   
   On posera $u'(x)=xe^{x^2}$ et $v(x)=x^2$
5. $\displaystyle \int_{e}^{e^2} ln(t) \,dx$
6. $\displaystyle \int_{1}^2 \dfrac{ln(t)}{t^2} \,dx$

1. Montrer que pour tout $t\in [0;~+\infin[$: $$1-t\leq \dfrac{1}{1+t} \leq 1-t+t^2$$
2. En déduire que pour tout $x\in [0;~+\infin[$: $$x-\dfrac{x^2}{2}\leq ln(1+x) \leq x-\dfrac{x^2}{2}+\dfrac{x^3}{3}$$
3. Utiliser le résultat précédent pour déterminer $$\lim\limits_{x \to 0 }\dfrac{ln(1+x)}{x}$$
4. Déterminer un encadrement de $ln(2)$ et vérifier le résultat à l'aide d'une calculatrice.

On considère la fonction $f$ de courbe représentative $C_f$ définie sur $]-1;~+\infin[$ par:$$f(x)=ln(1+x)$$. On a découpé l'intervalle $[2;~6]$ en 4 intervalles de longueur 1.

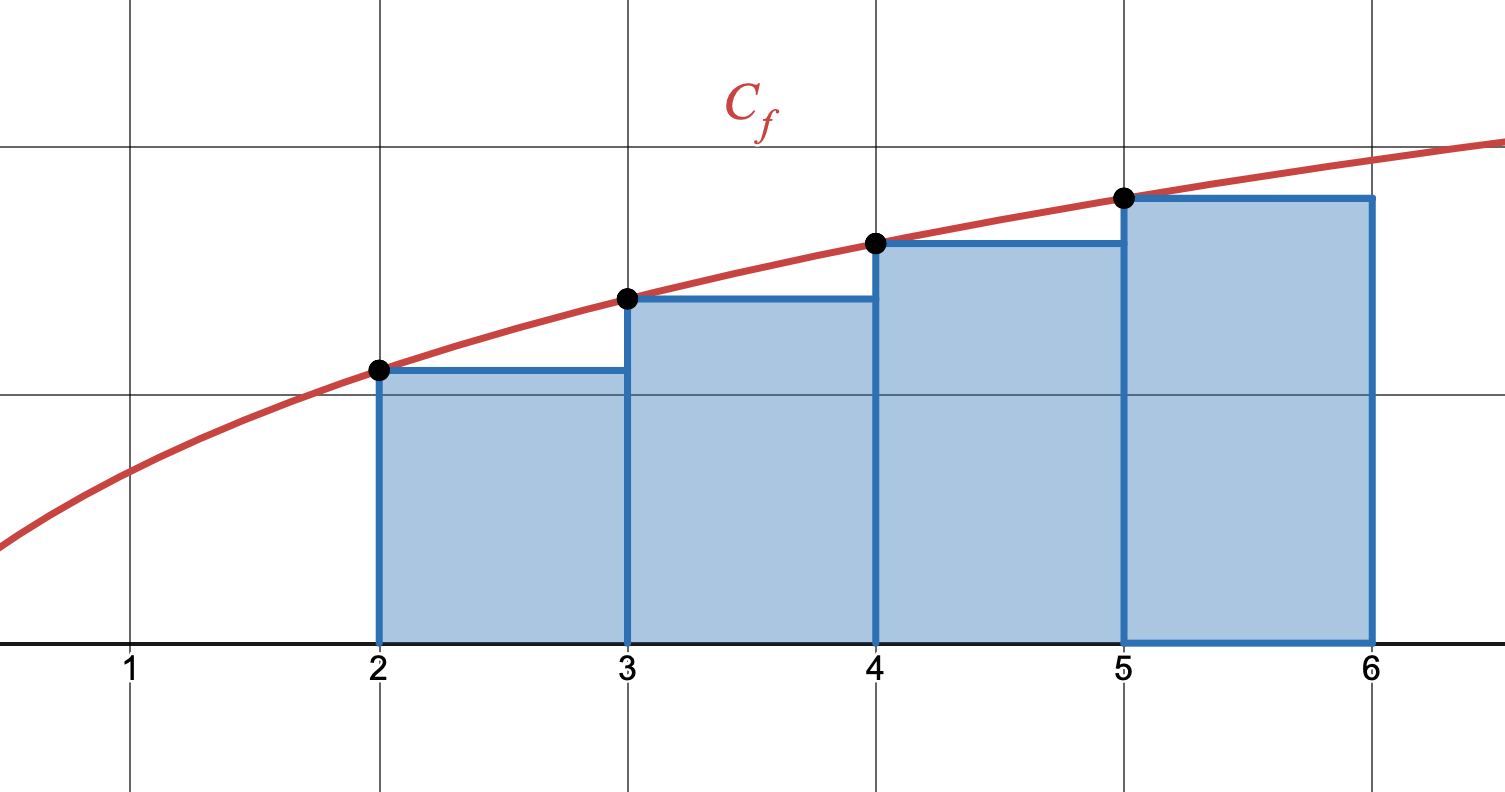
I. Rectangles à gauche

Chacun des rectangles suivants a pour hauteur respectivement $f(2),~f(3),~f(4),~f(5)$

1. Montrer que l'aire formée par les rectangles vaut $ln(360)$ unités d'aire.
2. En déduire une relation entre la valeur précédente et $\displaystyle \int_{2}^{6} ln(1+x) \,dx$

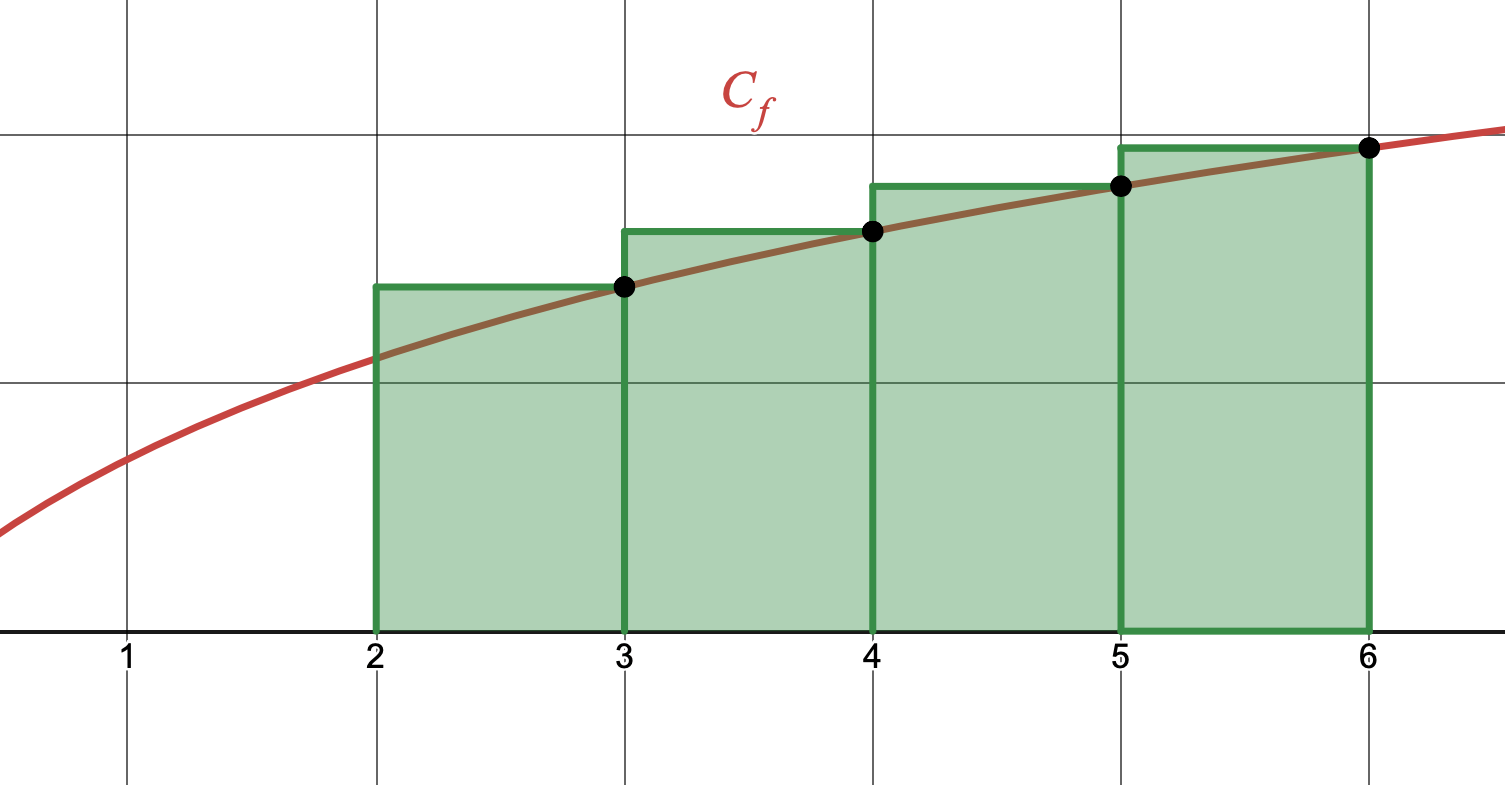
II. Rectangles à droite

Chacun des rectangles suivants a pour hauteur respectivement $f(3),~f(4),~f(5),~f(6)$

1. Montrer que l'aire formée par les rectangles vaut $ln(840)$ unités d'aire.
2. En déduire une relation entre la valeur précédente et $\displaystyle \int_{2}^{6} ln(1+x) \,dx$
3. En déduire grâce aux deux premières parties un encadrement de $\displaystyle \int_{2}^{6} ln(1+x) \,dx$

III. Rectangles au milieu

Chacun des rectangles suivants a pour hauteur respectivement $f(\frac{3}{2}),~f(\frac{5}{2}),~f(\frac{7}{2}),~f(\frac{9}{2})$

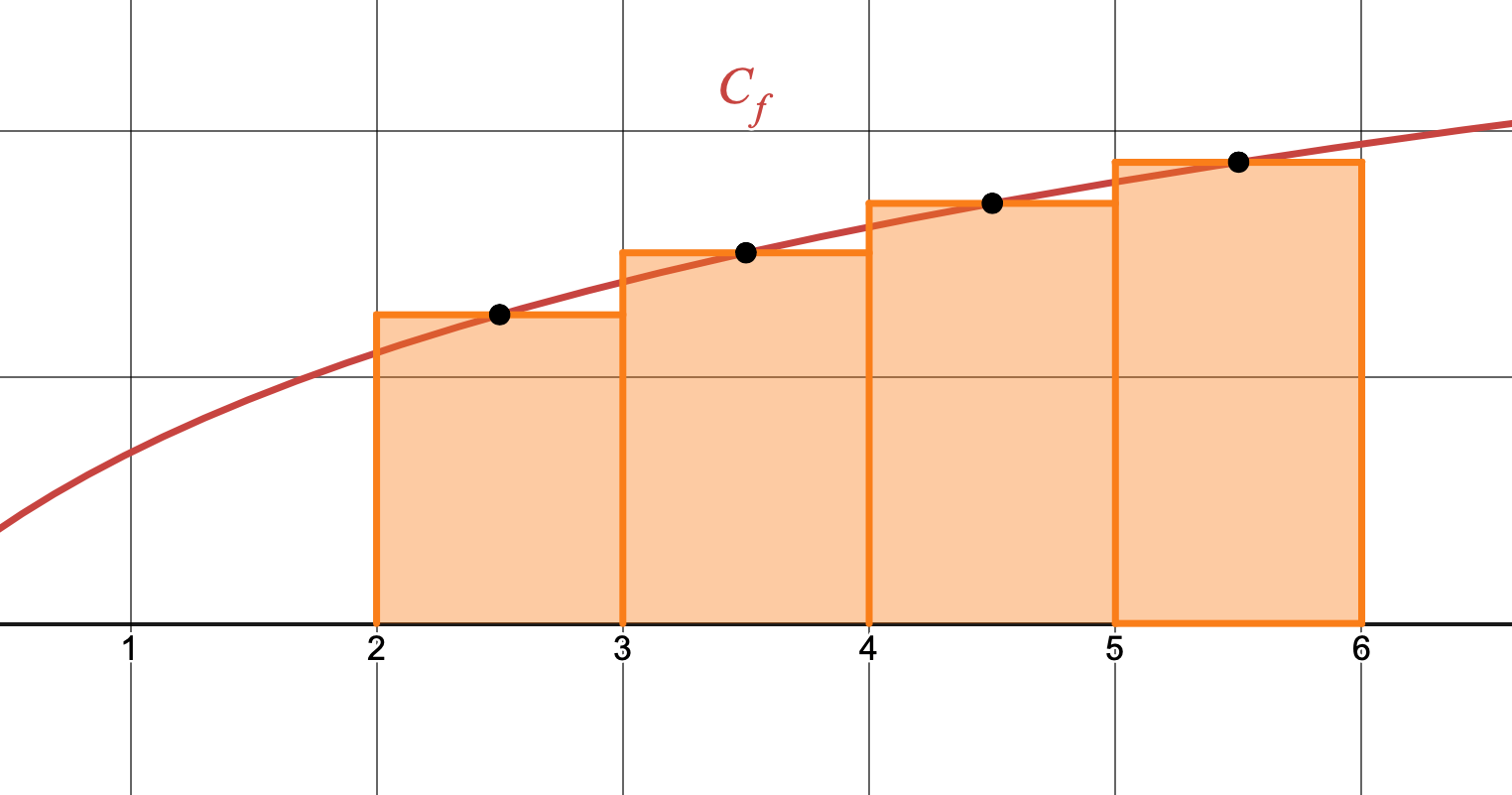
1. Montrer que l'aire formée par les rectangles vaut $ln(\dfrac{9009}{16}))$ unités d'aire. Que représente cette valeur par rapport à $\displaystyle \int_{2}^{6} ln(1+x) \,dx$?
2. Calculer $\displaystyle \int_{2}^{6} ln(1+x) \,dx$ à l'aide d'une intégration par parties et commenter le résultat précédent.

On considère l'intégrale:$$K=\displaystyle \int_0^{\pi} e^{x}cos(2x) \,dx$$

1. À l'aide de deux intégrations par parties successives montrer que $K=\dfrac{e^{\pi}-1}{5}$.
2. Soit $I=\displaystyle \int_0^{\pi} e^{x}cos^2(x) \,dx$ et $J=\displaystyle \int_0^{\pi} e^{x}sin^2(x) \,dx$
   Calculer $I+J$.
3. On rappelle que pour tous nombres réels $a$ et $b$, $cos(a+b)=cos(a)cos(b)-sin(a)sin(b)$. En utilisant cette identité, prouver que $I-J=K$.
4. En déduire les valeurs de $I$ et $J$.
5. Utiliser à nouveau l'identité $cos(a+b)=cos(a)cos(b)-sin(a)sin(b)$ pour montrer que $cos^2(x)=\dfrac{1+cos(2x)}{2}$ et $sin^2(x)=\dfrac{1-cos(2x)}{2}$.
   Retrouver directement les valeurs de $I$ et $J$ à l'aide de ce résultat et de la première question.

Les courbes $C_f$ et $C_g$ représentent respectivement les fonctions $f$ et $g$ définies sur $]0;~+\infin[$ par: $$f(x)=ln(x)~~~~g(x)=(ln~x)^2$$ On cherche à déterminer l'aire de la partie hachurée $\mathscr{A}$.

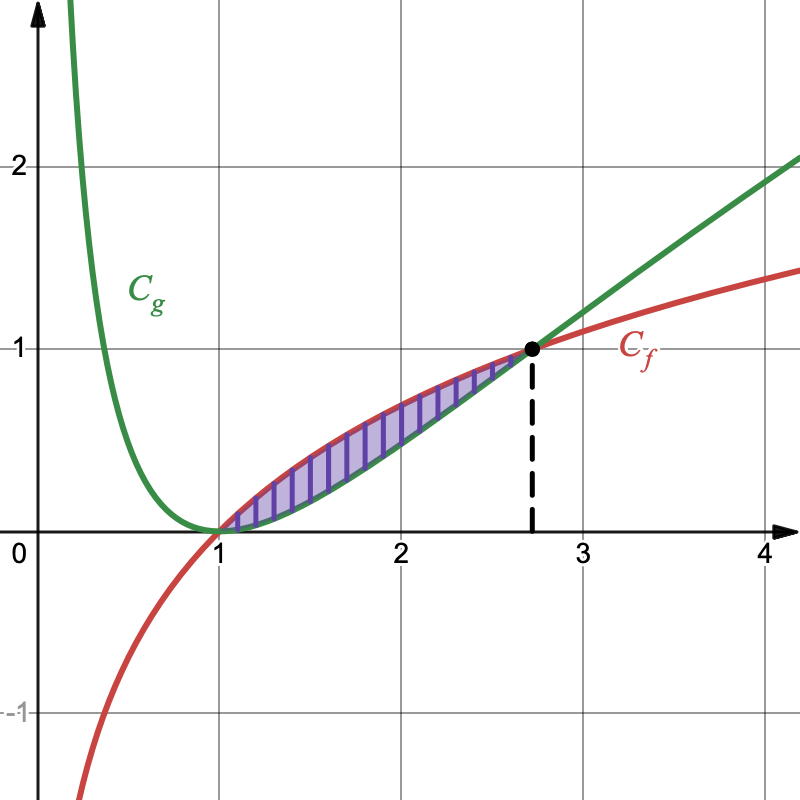
On note $I=\displaystyle \int_1^e ln(x) \,dx$ et $J=\displaystyle \int_1^e (ln~x)^2 \,dx$

1. Verifier que la fonction $F$ définie sur $]0;~+\infin[$ par $F(x)=xln(x)-x$ est une primitive de la fonction logarithme népérien. En déduire $I$.
2. Démontrer à l'aide d'une intégration par parties que $J=e-2I$.
3. En déduire $J$.
4. Déterminer les coordonnés des points d'intersection de $C_f$ et $C_g$.
5. Donner la valeur de $\mathscr{A}$.

1. Supposons qu'une voiture se déplace sur une autoroute et que sa vitesse (en mètres par seconde) après $t$ heures est donnée par la fonction:$$v(t) = 6t^3 - 27t^2 + 36t$$ pour $t$ dans l'intervalle $[0, 3]$ (c'est-à-dire pendant les 3 premières heures de son trajet).
   Calculer la vitesse moyenne de la voiture pendant les 3 premières heures de son trajet.
2. Supposons un pont suspendu modélisé par la fonction $y = \dfrac{e^{0.05x} + e^{-0.05x}}{2}$ sur l'intervalle $[-50, 50]$ mètres.
   Calculer la hauteur moyenne de la ligne du pont sur cet intervalle.
3. On considère la fonction définie par $p(x)=\dfrac{1}{1+e^{-0,2x}}$ sur $[0;~+\infin[$.
   1. Vérifier que pour tout $x\geq 0$:$$p(x)=\dfrac{e^{0,2x}}{1+e^{0,2x}}$$
   2. En déduire la valeur moyenne de $p$ sur l'intervalle $[8;~10]$