Les exercices
sur 7 exercices complétés
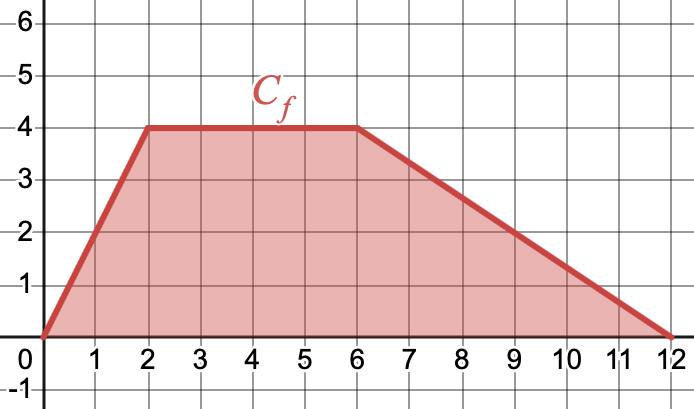
- Déterminer les aires rouges et violettes ci-dessus.
- Exprimer ces deux aires à l'aide de la notation intégrale $\displaystyle \int_a^b f(x)\,dx$
Calculer géométriquement les intégrales suivantes après avoir tracé la courbe représentative de chaque fonction sur l'intervalle considéré.
- $\displaystyle \int_{-2}^3 4\,dx$
- $\displaystyle \int_0^2 x\,dx$
- $\displaystyle \int_1^4 -2x+10\,dx$
- $\displaystyle \int_{-3}^3 |x|\,dx$
PARTIE A
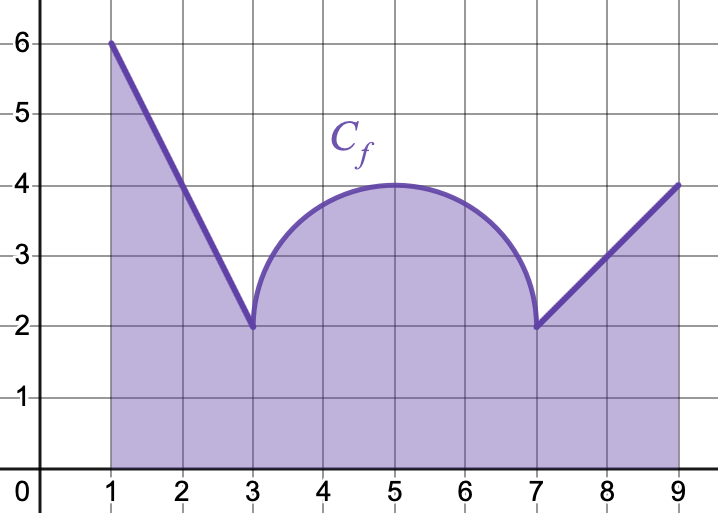
Calculer graphiquement les intégrales suivantes:
- $\displaystyle \int_{-2}^{-1} f(x)\,dx$
- $\displaystyle \int_{-4}^0 f(x)\,dx$
- $\displaystyle \int_{-1}^5 f(x)\,dx$
- $\displaystyle \int_{-2}^2 f(x)\,dx$
PARTIE B
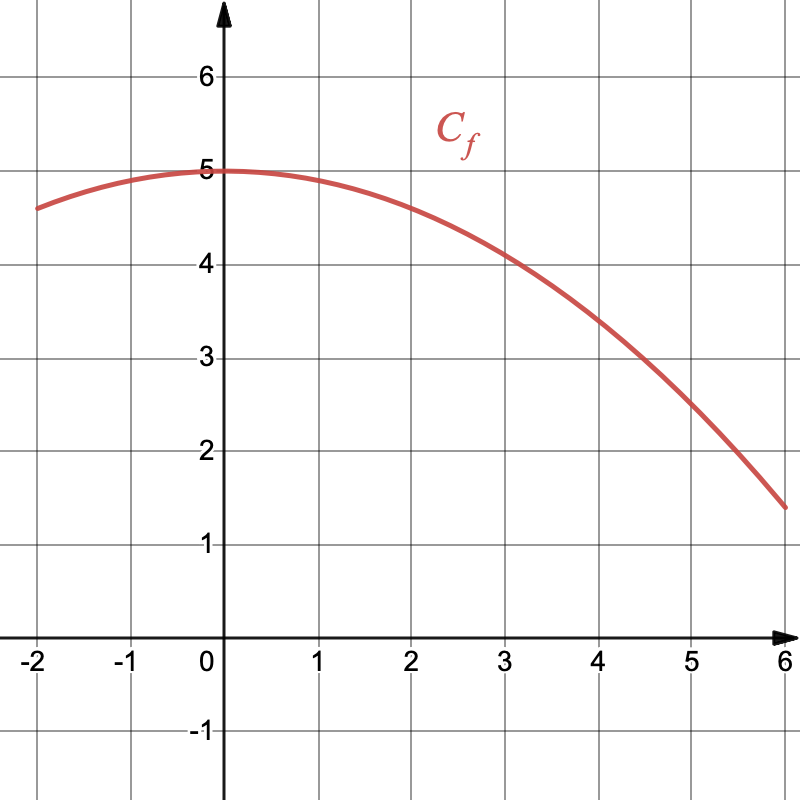
On considère la courbe de $f$ suivante:
- Déterminer graphiquement un encadrement de $\displaystyle \int_{-2}^6 f(x)\,dx$
- En réalité $f(x)=-\frac{1}{10}x^2+5$, déterminer $\displaystyle \int_{-2}^6 f(x)\,dx$
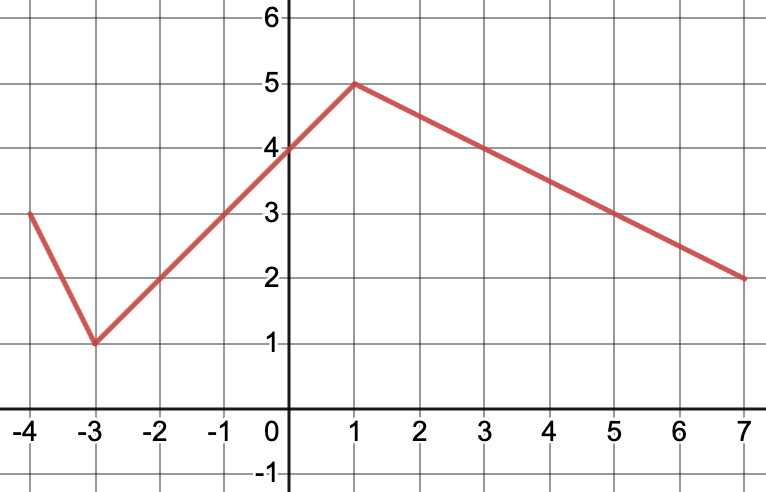
Déterminer le signe des intégrales suivantes sans faire de calcul:
- $\displaystyle \int_{-1}^{2} \dfrac{x^2+1}{x^2} \,dx$
- $\displaystyle \int_{0}^{4} e^{-x} \,dx$
- $\displaystyle \int_{-1}^{-5} -3x^2 \,dx$
- $\displaystyle \int_{0,1}^{0,5} \dfrac{ln(x)}{1-x} \,dx$
Pour chacune des fonctions suivantes, vérifier que la fonction en majuscule est une primitive de la fonction donnée puis calculer l'intégrale proposée.
- $f(x)=ln(x)$ et $F(x)=xln(x)-x$ puis $\displaystyle \int_{4}^{10} ln(x) \,dx$
- $g(x)=\dfrac{1}{x^3}$ et $G(x)=\dfrac{-1}{2x^2}$ puis $\displaystyle \int_{-4}^{-1} \dfrac{1}{x^3} \,dx$
- $h(x)=(x-1)(x+3)$ et $H(x)=\dfrac{x^3}{3}+x^2-3x+1$ puis $\displaystyle \int_{-2}^{3} (x-1)(x+3) \,dx$
- $j(x)=e^{-2x}-xe^{x^2}$ et $J(x)=-\dfrac{e^{-2x}}{2}-\dfrac{e^{x^2}}{2}$ puis $\displaystyle \int_{0}^{5} (e^{-2x}-xe^{x^2}) \,dx$
Calculer les intégrales suivantes
- $\displaystyle \int_{1}^5 \sqrt{2} \,dx$
- $\displaystyle \int_{-1}^3 3x-5\,dx$
- $\displaystyle \int_0^1 x^3-3x^2+5x-10\,dx$
- $\displaystyle \int_{-3}^3 |x|\,dx$
On considère la fonction définie sur $[0;~+\infin[$ par:$$\displaystyle \int_{0}^x ln(t+1) \,dt$$
- Justifier que pour tout $x\in [0;~+\infin[$, $F(x)\geq 0$.
- Donner une interprétation graphique de $F(1)$ et $F(2)$ puis les comparer.
- Exprimer $F(5)-F(2)$ à l'aide d'une intégrale.
- Calculer $F'(x)$ pour tout $x\in [0;~+\infin[$ et en déduire les variations de $F$ sur cet intervalle.
Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire
Calcul intégral
Fiche de synthèse
Contenu Complet Premium
Pour accéder au contenu complet de cette fiche de cours, vous devez vous abonner à notre offre premium.
Avec l'abonnement premium :
- Fiches de cours complètes
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Vidéos explicatives détaillées