Orthogonalité et distances dans l'espace
Base de l'espace
On appelle base orthonormée de l'espace 3 vecteurs linéairement indépendants $\vec{i}$, $\vec{j}$, $\vec{k}$ tels que: $\vec{i}.\vec{j}=0$, $\vec{j}.\vec{k}=0$, $\vec{i}.\vec{k}=0$ et $||\vec{i}||=||\vec{j}||=||\vec{k}||=1$
Orthogonalité dans l'espace
- Deux droites sont orthogonales lorsque leurs parallèles respectives passant par un même point sont perpendiculaires.
- Deux vecteurs non nuls sont orthogonaux lorsque les droites dirigées par ces vecteurs sont orthogonales.
- Une droite est orthogonale à un plan lorsqu'elle est orthogonale à toutes les droites de ce plan.
- Une droite est orthogonale à un plan si elle est orthogonale à deux droites sécantes de ce plan.
Plans orthogonaux dans l'espace
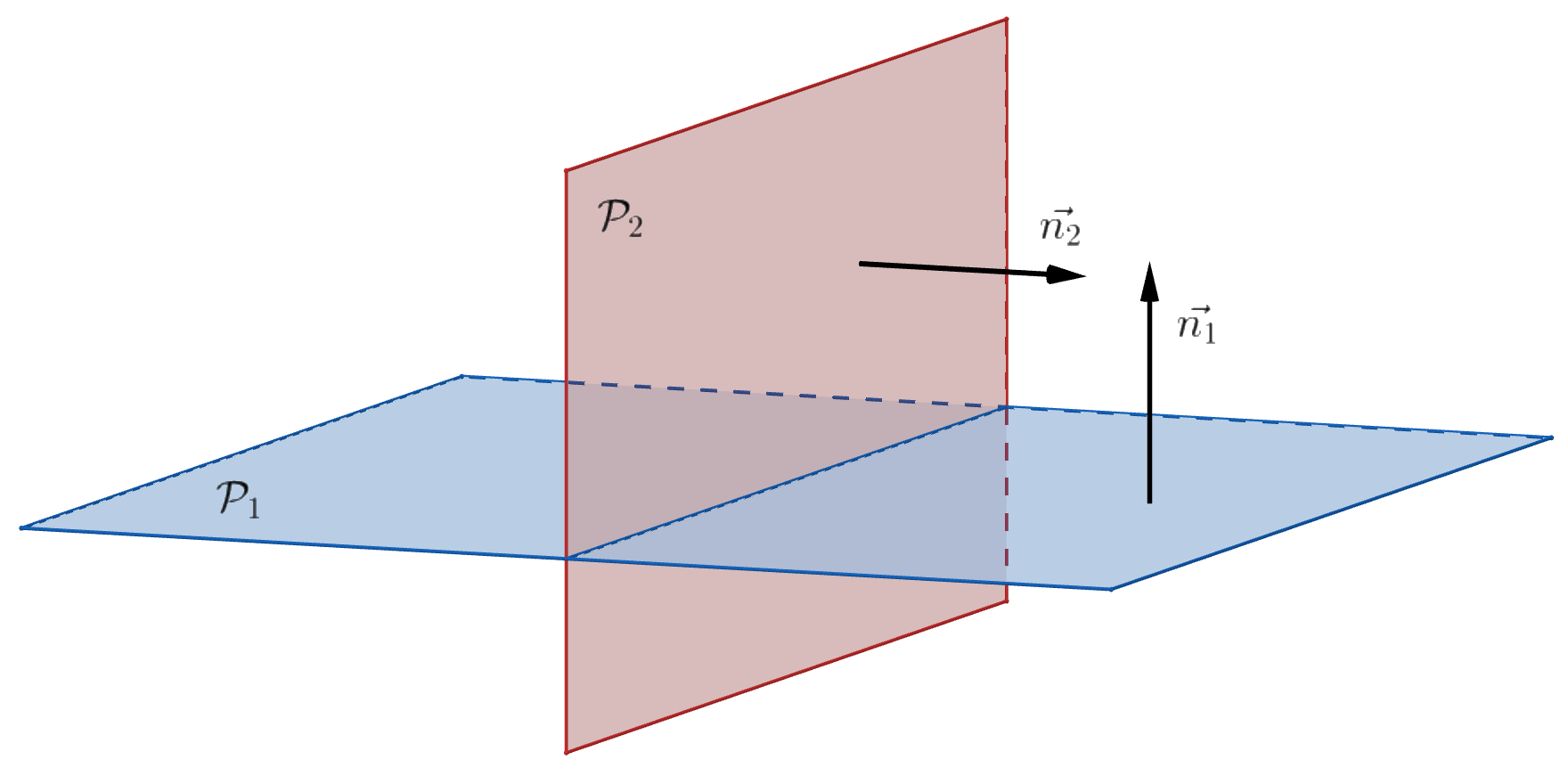
On considère les plans $\cal{P_1}$ et $\cal{P_2}$. $\vec{n_1}$ est un vecteur normal de $\cal{P_1}$ et $\vec{n_1}$ un vecteur normal de $\cal{P_2}$.
$\cal{P_1}$ et $\cal{P_2}$ sont orthogonaux si et seulement si $\vec{n_1}$ et $\vec{n_2}$ sont orthogonaux.
Plans parallèles dans l'espace
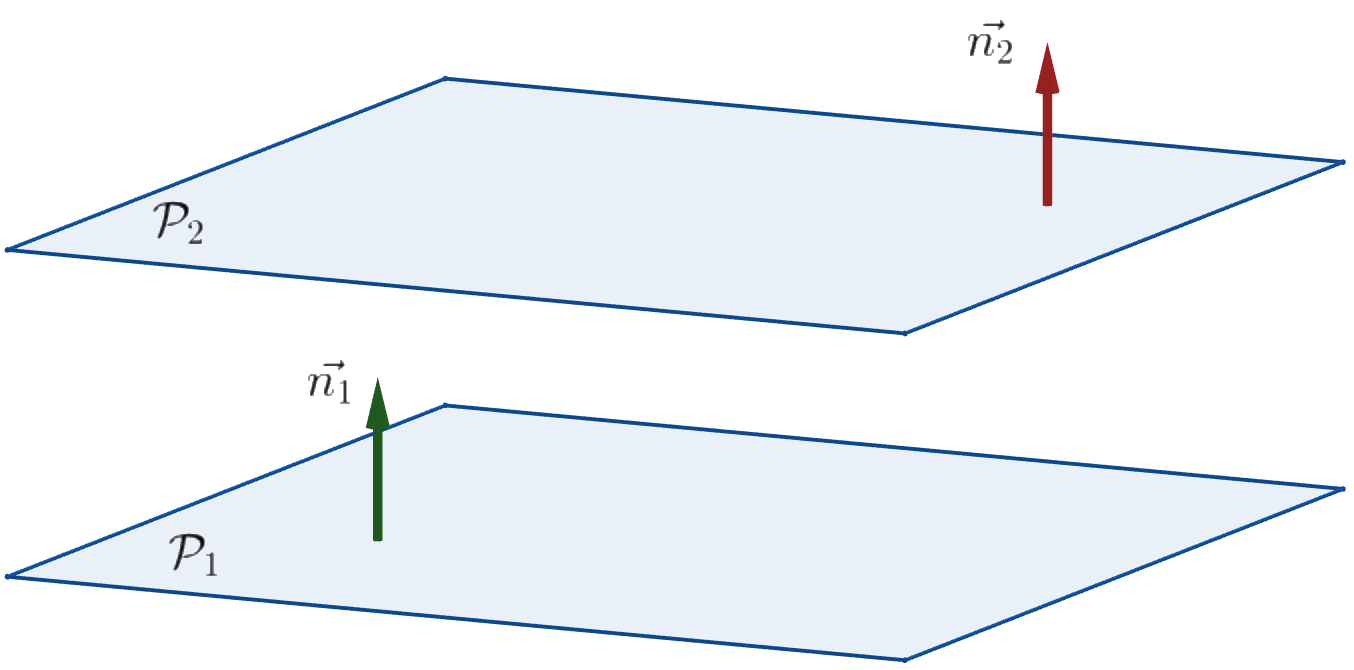
On considère les plans $\cal{P_1}$ et $\cal{P_2}$. $\vec{n_1}$ est un vecteur normal de $\cal{P_1}$ et $\vec{n_1}$ un vecteur normal de $\cal{P_2}$.
$\cal{P_1}$ et $\cal{P_2}$ sont parallèles si et seulement si $\vec{n_1}$ et $\vec{n_2}$ sont colinéaires.
Produit scalaire dans l'espace
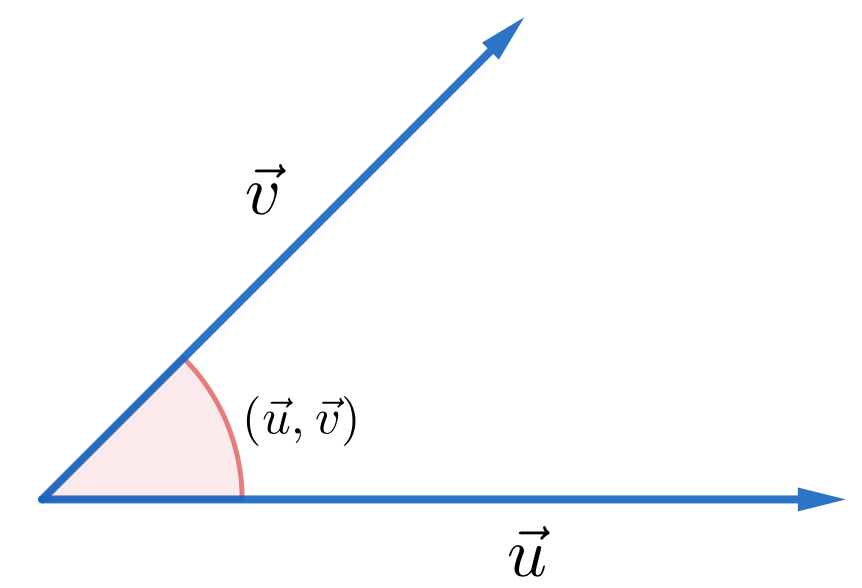
Soit $\vec{u}$ et $\vec{v}$ deux vecteurs non nuls de l'espace, leur produit scalaire est défini par: $$\vec{u}.\vec{v}=||\vec{u}||\times ||\vec{v}||\times cos(\vec{u}; \vec{v})$$
Produit scalaire dans l'espace
Soit $\vec{u}$ et $\vec{v}$ deux vecteurs non nuls de l'espace, leur produit scalaire est défini par: $$\vec{u}.\vec{v}=||\vec{u}||\times ||\vec{v}||\times cos(\vec{u}, \vec{v})$$
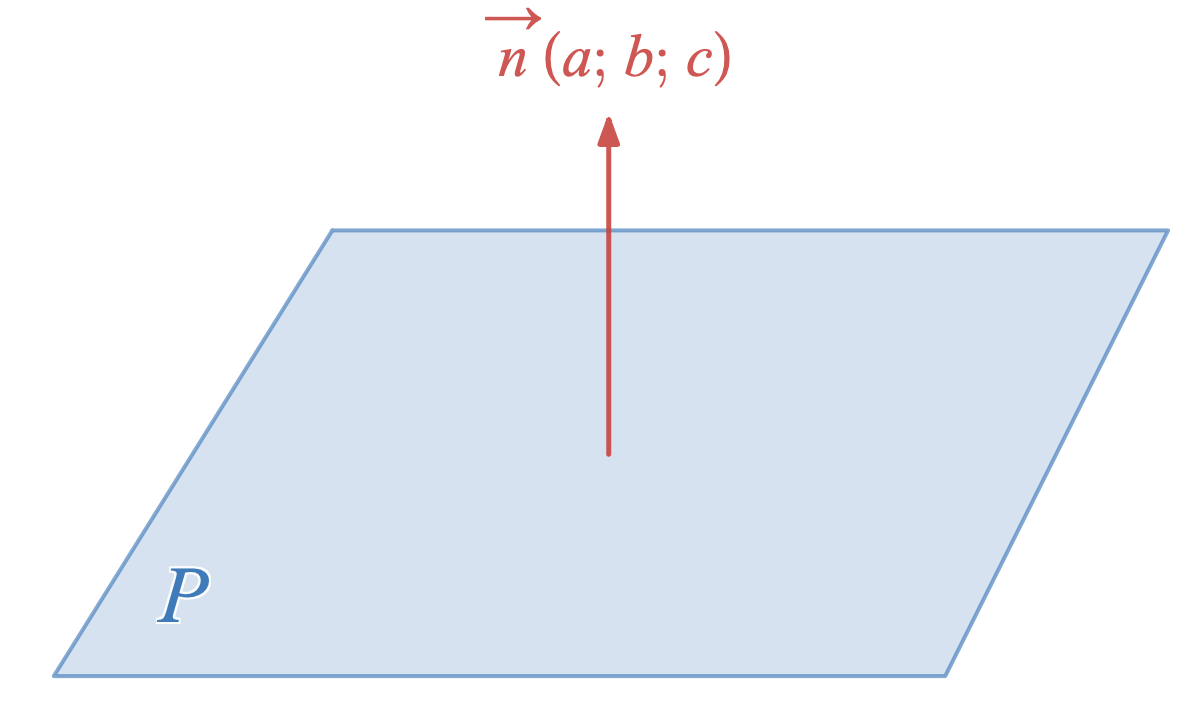
Equation cartésienne d'un plan
Soit $\vec{n}(a;~b,~c)$ un vecteur normal à un plan $P$. Alors une équation cartésienne de ce plan est: $$ax+by+cz+d=0$$.
Distance d'un point à un plan
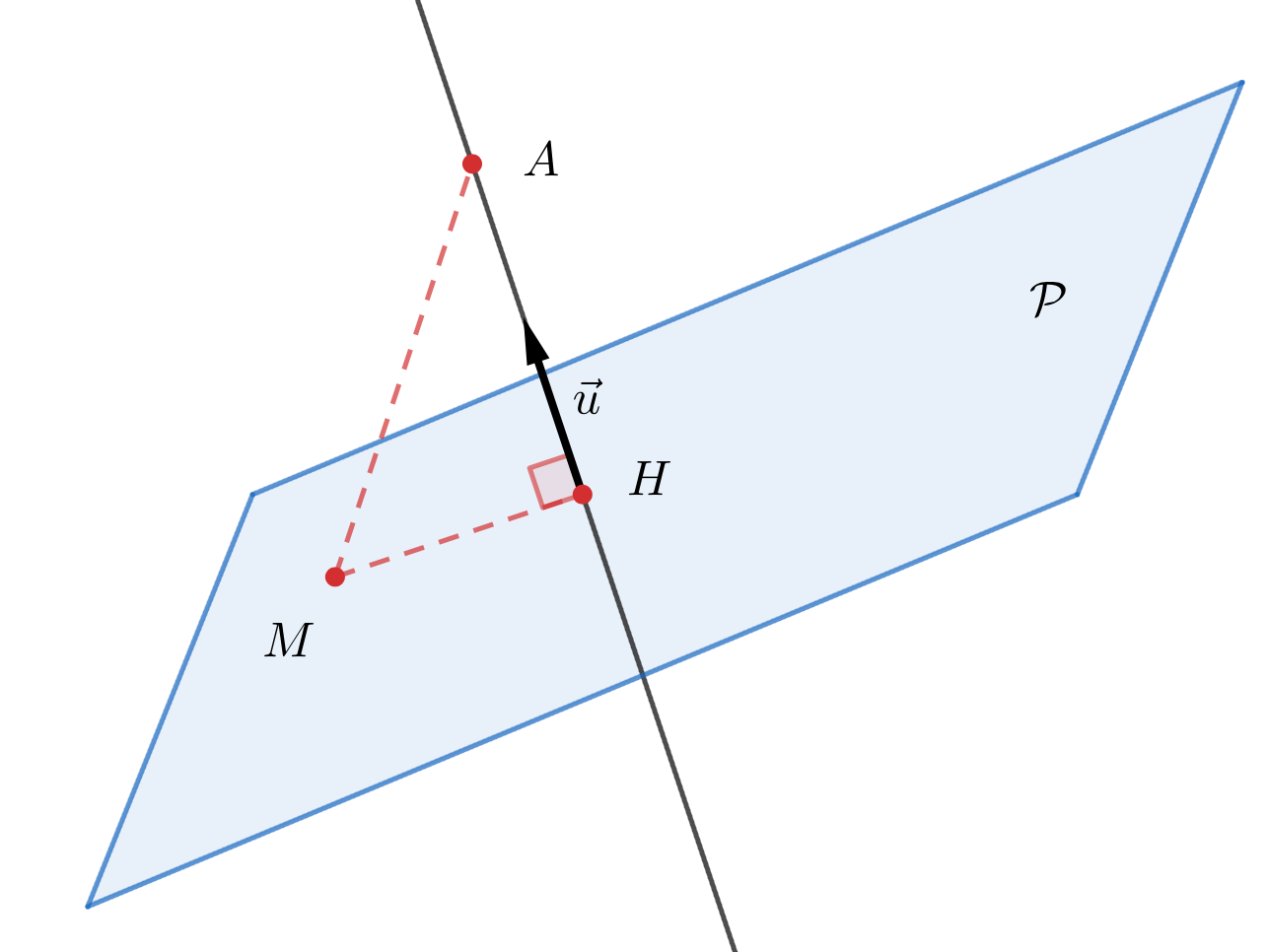
Soit $\cal{P}$ un plan de l'espace et $A$ un point. On note $H$ le projeté orthogonal du point $A$ sur ce plan, et $\vec{n}$ un vecteur normal de $\cal{P}$.
- La distance du point $A$ au plan $\cal{P}$ est la plus petite longueur $AM$ avec $M \in \cal{P}$
- En notant $d(A, \cal{P})$ la distance du point $A$ au plan $\cal{P}$, on a $d(A, \mathcal{P})=AH$
- Si $\cal{P}$ a pour équation cartésienne $ac+by+cz+d=0$, $A(x_A;~y_A;~z_A)$ et $M(x;~y;~z)$ un point du plan $\cal{P}$, alors: $$d(A, \mathcal{P})=\frac{|\overrightarrow{AM}.\vec{n}|}{||\vec{n}||}=\frac{|ax_A+by_A+cz_A+d|}{\sqrt{a^2+b^2+c^2}}$$
Distance d'un point à une droite
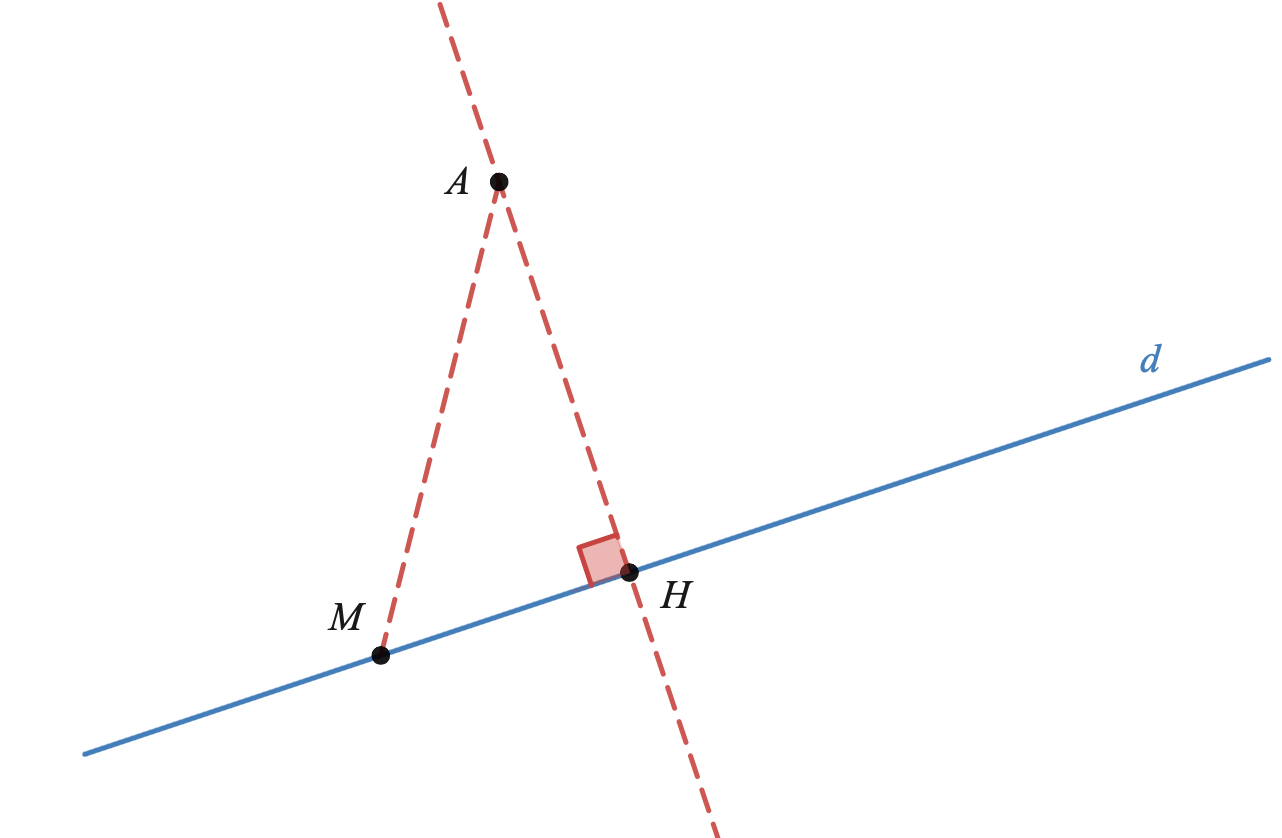
Soit $\cal{D}$ une droite de l'espace et $A$ un point.
- La distance du point $A$ à la droite $\cal{D}$ est la plus petite longueur $AM$ avec $M \in \cal{D}$
- Soit $H$ le projeté orthogonal du point $A$ sur $\cal{D}$. En notant $d(A, \cal{D})$ la distance du point $A$ à la droite $\cal{D}$, on a $d(A, \mathcal{D})=AH$