Sujets de Bac
2024
Suites et Limites
Filtrer par chapitre
Amerique Du Nord 21 Mai 2024 Jour 1
1 exercice
Pour tout entier naturel $ n $, on considère les intégrales suivantes : $$I_n = \int_{0}^{\pi} e^{-nx}\sin(x)\,dx, \quad J_n = \int_{0}^{\pi} e^{-nx}\cos(x)\,dx.$$
- Calculer $ I_0 $.
-
- Justifier que, pour tout entier naturel $ n $, on a $ I_n \geq 0 $.
- Montrer que, pour tout entier naturel $ n $, on a $ I_{n+1} - I_n \leq 0 $.
- Déduire des deux questions précédentes que la suite $ (I_n) $ converge.
-
- Montrer que, pour tout entier naturel $ n $, on a : $$ I_n \leq \int_{0}^{\pi} e^{-nx}\,dx. $$
- Montrer que, pour tout entier naturel $ n \geq 1 $, on a : $$ \int_{0}^{\pi} e^{-nx}\,dx = \frac{1 - e^{-n\pi}}{n}. $$
- Déduire des deux questions précédentes la limite de la suite $ (I_n) $.
-
- En intégrant par parties l’intégrale $ I_n $ de deux façons différentes, établir les deux relations suivantes, pour tout entier naturel $ n \geq 1 $ : $$ I_n = 1 + e^{-n\pi} - nJ_n \quad \text{et} \quad I_n = \frac{1}{n}J_n. $$
- En déduire que, pour tout entier naturel $ n \geq 1 $, on a : $$ I_n = \frac{1 + e^{-n\pi}}{n^2 + 1}. $$
- On souhaite obtenir le rang $ n $ à partir duquel la suite $ (I_n) $ devient inférieure à 0,1.
Recopier et compléter la cinquième ligne du script Python ci-dessous avec la commande appropriée.
Amerique Du Nord 22 Mai 2024 Jour 2
1 exercice
On considère la fonction $ g $ définie sur l’intervalle $ [0 ; 1] $ par : $$ g(x) = 2x - x^2. $$
- Montrer que la fonction $ g $ est strictement croissante sur l’intervalle $ [0 ; 1] $ et préciser les valeurs de $ g(0) $ et de $ g(1) $.
- On considère la suite $ (u_n) $ définie par
$$
\begin{cases}
u_0 = \frac{1}{2} \\
u_{n+1} = g(u_n)
\end{cases}
$$ pour tout entier naturel $ n $.
- Calculer $ u_1 $ et $ u_2 $.
- Démontrer par récurrence que, pour tout entier naturel $ n $, on a : $ 0 < u_n < u_{n+1} < 1 $.
- En déduire que la suite $ (u_n) $ est convergente.
- Déterminer la limite $ \ell $ de la suite $ (u_n) $.
- On considère la suite $ (v_n) $ définie pour tout entier naturel $ n $ par $ v_n = \ln(1 - u_n) $.
- Démontrer que la suite $ (v_n) $ est une suite géométrique de raison 2 et préciser son premier terme.
- En déduire une expression de $ v_n $ en fonction de $ n $.
- En déduire une expression de $ u_n $ en fonction de $ n $ et retrouver la limite déterminée à la question 5.
- Recopier et compléter le script Python ci-dessous afin que celui-ci renvoie le rang $ n $ à partir duquel la suite dépasse 0,95.
Asie 10 Juin 2024 Jour 1
1 exercice
Pour chacune des affirmations suivantes, préciser si elle est vraie ou fausse puis justifier la réponse donnée.
Toute réponse non argumentée ne sera pas prise en compte.
- Affirmation 1 : Toute suite décroissante et minorée par 0 converge vers 0.
- On considère une suite $ (u_n) $ définie sur $ \mathbb{N} $ telle que, pour tout entier $ n $, on a
$$
u_n \leq \frac{-9^n + 3^n}{7^n}.
$$
Affirmation 2 : $ \lim_{n \to +\infty} u_n = -\infty $. - On considère la fonction suivante écrite en langage Python :
def terme(N) : U = 1 for i in range(N) : U = U + i return UAffirmation 3 :terme(4)renvoie la valeur 7. - Lors d’un concours, le gagnant a le choix entre deux prix :
- Prix A : il reçoit 1 000 euros par jour pendant 15 jours ;
- Prix B : il reçoit 1 euro le 1er jour, 2 euros le 2e jour, 4 euros le 3e jour et pendant 15 jours la somme reçue double chaque jour.
- On considère la suite $ (v_n) $ définie pour tout entier $ n \geq 1 $ par
$$
v_n = \int_{1}^{n} \ln x \, dx.
$$
Affirmation 5 : La suite $ (v_n) $ est croissante.
Asie 11 Juin 2024 Jour 2
2 exercices
On considère la fonction $ f $ définie sur $ ]0 ; +\infty[ $ par :
$$
f(x) = x^2 - x\ln(x).
$$
On admet que $ f $ est deux fois dérivable sur $ ]0 ; +\infty[ $.
On note $ f' $ la fonction dérivée de la fonction $ f $ et $ f'' $ la fonction dérivée de la fonction $ f' $.
Partie A : Étude de la fonction $ f $
- Déterminer les limites de la fonction $ f $ en 0 et en $ +\infty $.
- Pour tout réel $ x $ strictement positif, calculer $ f'(x) $.
- Montrer que pour tout réel $ x $ strictement positif : $$ f''(x) = \frac{2x - 1}{x}. $$
- Étudier les variations de la fonction $ f' $ sur $ ]0 ; +\infty[ $, puis dresser le tableau des variations de la fonction $ f' $ sur $ ]0 ; +\infty[ $.
On veillera à faire apparaître la valeur exacte de l’extrémum de la fonction $ f' $ sur $ ]0 ; +\infty[ $.
Les limites de la fonction $ f' $ aux bornes de l’intervalle de définition ne sont pas attendues. - Montrer que la fonction $ f $ est strictement croissante sur $ ]0 ; +\infty[ $.
Partie B : Étude d’une fonction auxiliaire pour la résolution de l’équation $ f(x) = x $
On considère dans cette partie la fonction $ g $ définie sur $ ]0 ; +\infty[ $ par :
$$
g(x) = x - \ln(x).
$$
On admet que la fonction $ g $ est dérivable sur $ ]0 ; +\infty[ $, on note $ g' $ sa dérivée.
- Pour tout réel strictement positif, calculer $ g'(x) $, puis dresser le tableau des variations de la fonction $ g $.
Les limites de la fonction $ g $ aux bornes de l’intervalle de définition ne sont pas attendues. - On admet que 1 est l’unique solution de l’équation $ g(x) = 1 $.
Résoudre, sur l’intervalle $ ]0 ; +\infty[ $, l’équation $ f(x) = x $.
Partie C : Étude d’une suite récurrente
On considère la suite $ (u_n) $ définie par $ u_0 = \frac{1}{2} $ et pour tout entier naturel $ n $, $$ u_{n+1} = f(u_n) = u_n^2 - u_n\ln(u_n). $$
- Montrer par récurrence que pour tout entier naturel $ n $ : $$ \frac{1}{2} \leq u_n \leq u_{n+1} \leq 1. $$
- Justifier que la suite $ (u_n) $ converge.
On appelle $ \ell $ la limite de la suite $ (u_n) $ et on admet que $ \ell $ vérifie l’égalité $ f(\ell) = \ell $. - Déterminer la valeur de $ \ell $.
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. Chaque réponse doit être justifiée. Une réponse non justifiée ne rapporte aucun point.
-
Soit $ (u_n) $ une suite définie pour tout entier naturel $ n $ et vérifiant la relation suivante :
$$ \dfrac{1}{2} < u_n \leq \dfrac{3n^2 + 4n + 7}{6n^2 + 1} \text{ pour tout entier naturel } n $$.
Affirmation 1 : $ \lim\limits_{n \to +\infty} u_n = \dfrac{1}{2} $.
-
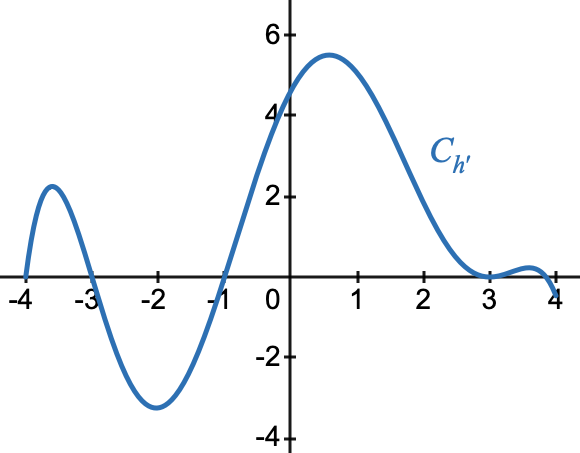
Soit $ h $ une fonction définie et dérivable sur l’intervalle $[-4 ; 4]$. La représentation graphique $ \mathcal{C}_{h'} $ de sa fonction dérivée $ h' $ est donnée ci-dessous.
Affirmation 2 : La fonction $ h $ est convexe sur $[-1 ; 3]$.
-
Le code d’un immeuble est composé de 4 chiffres (qui peuvent être identiques) suivis de deux lettres distinctes parmi A, B et C (exemple : 1232BA).
Affirmation 3 : Il existe 20 634 codes qui contiennent au moins un 0.
-
On considère la fonction $ f $ définie sur $ \left] 0 ; +\infty \right[ $ par $ f(x) = x \ln x $.
Affirmation 4 : La fonction $ f $ est une solution sur $ \left] 0 ; +\infty \right[ $ de l’équation différentielle
$$ x y' - y = x $$.
Centres Etrangers 5 Juin 2024 Jour 1
1 exercice
On considère la fonction $ f $ définie sur l’intervalle $ [0 ; 1] $ par : $$f(x) = 2xe^{-x}.$$
On admet que la fonction $ f $ est dérivable sur l’intervalle $ [0 ; 1] $.
-
- Résoudre sur l’intervalle $ [0 ; 1] $ l’équation $ f(x) = x $.
- Démontrer que, pour tout $ x $ appartenant à l’intervalle $ [0 ; 1] $, $$ f'(x) = 2(1 - x)e^{-x}. $$
- Donner le tableau de variations de la fonction $ f $ sur l’intervalle $ [0 ; 1] $.
On considère la suite $ (u_n) $ définie par $ u_0 = 0,1 $ et pour tout entier naturel $ n $, $$ u_{n+1} = f(u_n). $$
-
- Démontrer par récurrence que, pour tout $ n $ entier naturel, $$ 0 \leq u_n < u_{n+1} \leq 1. $$
- En déduire que la suite $ (u_n) $ est convergente.
- Démontrer que la limite de la suite $ (u_n) $ est $ \ln(2) $.
-
- Justifier que pour tout entier naturel $ n $, $ \ln(2) - u_n $ est positif.
- On souhaite écrire un script Python qui renvoie une valeur approchée de $ \ln(2) $ par défaut à $ 10^{-4} $ près, ainsi que le nombre d’étapes pour y parvenir.
Recopier et compléter le script ci-dessous afin qu’il réponde au problème posé.def seuil() : n = 0 u = 0.1 while ln(2) - u ... 0.0001 : n = n + 1 u = ... return (u, n) - Donner la valeur de la variable $ n $ renvoyée par la fonction seuil().
Centres Etrangers 6 Juin 2024 Jour 2
1 exercice
Partie A
On considère la fonction $ f $ définie sur l’intervalle $ [0 ; +\infty[ $ par : $$ f(x) = \sqrt{x + 1}. $$
On admet que cette fonction est dérivable sur ce même intervalle.
- Démontrer que la fonction $ f $ est croissante sur l’intervalle $ [0 ; +\infty[ $.
- Démontrer que pour tout nombre réel $ x $ appartenant à l’intervalle $ [0 ; +\infty[ $ : $$ f(x) - x = \frac{-x^2 + x + 1}{\sqrt{x + 1} + x}. $$
- En déduire que sur l’intervalle $ [0 ; +\infty[ $ l’équation $ f(x) = x $ admet pour unique solution : $$ \ell = \frac{1 + \sqrt{5}}{2}. $$
Partie B
On considère la suite $ (u_n) $ définie par $ u_0 = 5 $ et pour tout entier naturel $ n $, par $ u_{n+1} = f(u_n) $ où $ f $ est la fonction étudiée dans la partie A.
On admet que la suite de terme général $ u_n $ est bien définie pour tout entier naturel $ n $.
- Démontrer par récurrence que pour tout entier naturel $ n $, on a : $$ 1 \leq u_{n+1} \leq u_n. $$
- En déduire que la suite $ (u_n) $ converge.
- Démontrer que la suite $ (u_n) $ converge vers $ \ell = \frac{1 + \sqrt{5}}{2} $.
- On considère le script Python ci-dessous :
1 from math import * 2 def seuil(n): 3 u = 5 4 i = 0 5 l = (1 + sqrt(5)) / 2 6 while abs(u - l) >= 10**(-n): 7 u = sqrt(u + 1) 8 i = i + 1 9 return iOn rappelle que la commande
abs(x)renvoie la valeur absolue de $ x $.- Donner la valeur renvoyée par
seuil(2). - La valeur renvoyée par
seuil(4)est 9.
Interpréter cette valeur dans le contexte de l’exercice.
- Donner la valeur renvoyée par
Metropole 19 Juin 2024 Jour 1
1 exercice
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. Chaque réponse doit être justifiée. Une réponse non justifiée ne rapporte aucun point.
-
On considère la fonction $f$ définie sur $\mathbb{R}$ par : $f(x)=5x\mathrm{e}^{-x}$.
On note $C_f$ la courbe représentative de $f$ dans un repère orthonormé.Affirmation 1 :
L'axe des abscisses est une asymptote horizontale à la courbe $C_f$.
Affirmation 2 :
La fonction $f$ est solution sur $\mathbb{R}$ de l'équation différentielle $(E)$ : $y' + y = 5\mathrm{e}^{-x}$.
-
On considère les suites $\left(u_n\right)$, $\left(v_n\right)$ et $\left(w_n\right)$, telles que, pour tout entier naturel $n$ : $$ u_n \leqslant v_n \leqslant w_n. $$
De plus, la suite $\left(u_n\right)$ converge vers $-1$ et la suite $\left(w_n\right)$ converge vers $1$.
Affirmation 3 :
La suite $\left(v_n\right)$ converge vers un nombre réel $\ell$ appartenant à l'intervalle $[-1; 1]$.
On suppose de plus que la suite $\left(u_n\right)$ est croissante et que la suite $\left(w_n\right)$ est décroissante.
Affirmation 4 :
Pour tout entier naturel $n$, on a alors : $u_0 \leqslant v_n \leqslant w_0$.
Metropole 20 Juin 2024 Jour 2
1 exercice
Les parties A et B sont indépendantes
Alain possède une piscine qui contient $50 ~\mathrm{m}^{3}$ d'eau. On rappelle que $1 ~\mathrm{m}^{3} = 1000 \mathrm{L}$.
Pour désinfecter l'eau, il doit ajouter du chlore.
Le taux de chlore dans l'eau, exprimé en $ \mathrm{mg} \cdot \mathrm{L}^{-1} $, est défini comme la masse de chlore par unité de volume d'eau. Les piscinistes préconisent un taux de chlore compris entre $1$ et $3~\mathrm{mg \cdot L}^{-1}$.
Sous l'action du milieu ambiant, notamment des ultraviolets, le chlore se décompose et disparaît peu à peu.
Alain réalise certains jours, à heure fixe, des mesures avec un appareil qui permet une précision à $0,01 ~\mathrm{mg \cdot L}^{-1}$. Le mercredi 19 juin, il mesure un taux de chlore de $0,70 ~\mathrm{mg \cdot L}^{-1}$.
Partie A : étude d'un modèle discret.
- Justifier que cet ajout de chlore fait augmenter le taux de $0,3, \mathrm{mg \cdot L}^{-1}$.
-
- Pour tout entier naturel $n$, on note $v_{n}$ le taux de chlore, en $ \mathrm{mg \cdot L}^{-1} $, obtenu avec ce nouveau protocole $n$ jours après le mercredi 19 juin. Ainsi $v_{0}=0,7$.
On admet que pour tout entier naturel $n$, $$ v_{n+1}=0,92 v_{n}+ 0,3. $$ - Montrer par récurrence que pour tout entier naturel $n$, $$ v_{n} \leqslant v_{n+1} \leqslant 4. $$
- Montrer que la suite $ (v_{n}) $ est convergente et calculer sa limite.
- Pour tout entier naturel $n$, on note $v_{n}$ le taux de chlore, en $ \mathrm{mg \cdot L}^{-1} $, obtenu avec ce nouveau protocole $n$ jours après le mercredi 19 juin. Ainsi $v_{0}=0,7$.
- À long terme, le taux de chlore sera-t-il conforme à la préconisation des piscinistes ? Justifier la réponse.
- Reproduire et compléter l'algorithme ci-après écrit en langage Python pour que la fonction
alerte_chlorerenvoie, lorsqu'il existe, le plus petit entier $n$ tel que $v_{n}> s$. - Quelle valeur obtient-on en saisissant l'instruction
alerte_chlore(3)? Interpréter ce résultat dans le contexte de l'exercice.
def alerte_chlore(s):
n = 0
u = 0.7
while ...:
n = ...
u = ...
return n
Partie B : étude d'un modèle continu.
Alain décide de faire appel à un bureau d'études spécialisées. Celui-ci utilise un modèle continu pour décrire le taux de chlore dans la piscine.
Dans ce modèle, pour une durée $x$ (en jours écoulés à compter du mercredi 19 juin), $f(x)$ représente le taux de chlore, en $ \mathrm{mg} \cdot \mathrm{L}^{-1} $, dans la piscine.
On admet que la fonction $f$ est solution de l'équation différentielle $(E)$ : $$ y'=-0,08 y+\frac{q}{50}, $$ où $q$ est la quantité de chlore, en grammes, rajoutée dans la piscine chaque jour.
- Justifier que la fonction $f$ est de la forme : $$ f(x)=C e^{-0,08 x}+\frac{q}{4}, $$ où $C$ est une constante réelle.
-
- Exprimer en fonction de $q$ la limite de $f$ en $+\infty$.
- On rappelle que le taux de chlore observé le mercredi 19 juin est égal à $0,7~\mathrm{mg \cdot L}^{-1}$.
On souhaite que le taux de chlore se stabilise à long terme autour de $2~\mathrm{mg \cdot L}^{-1}$. Déterminer les valeurs de $C$ et $q$ afin que ces deux conditions soient respectées.
Polynesie 19 Juin 2024 Jour 1
1 exercice
L'objectif de cet exercice est de conjecturer en partie A puis de démontrer en partie B le comportement d'une suite.
Les deux parties peuvent cependant être traitées de manière indépendante.
On considère la suite $\left(u_n\right)$ définie par $u_0 = 3$ et pour tout $n \in \mathbb{N}$ :
$$ u_{n+1} = \dfrac{4}{5 - u_n}. $$
Partie A
- Recopier et compléter la fonction Python suivante
suite(n)qui prend comme paramètre le rang $n$ et renvoie la valeur du terme $u_n$. - L'exécution de
suite(2)renvoie1.3333333333333333.
Effectuer un calcul pour vérifier et expliquer cet affichage. - À l'aide des affichages ci-dessous, émettre une conjecture sur le sens de variation et une conjecture sur la convergence de la suite $\left(u_n\right)$.
def suite(n):
u = ...
for i in range(n):
...
return u
| >> suite(2) | 1.3333333333333333 |
| >> suite(5) | 1.0058479532163742 |
| >> suite(10) | 1.0000057220349845 |
| >> suite(20) | 1.000000000005457 |
Partie B
On considère la fonction $f$ définie et dérivable sur l'intervalle $]-\infty~;~5[$ par :
$$ f(x) = \dfrac{4}{5 - x}. $$
Ainsi, la suite $\left(u_n\right)$ est définie par $u_0 = 3$ et pour tout $n \in \mathbb{N},: u_{n+1} = f\left(u_n\right)$.
- Montrer que la fonction $f$ est croissante sur l'intervalle $]-\infty~;~5[$.
- Démontrer par récurrence que pour tout entier naturel $n$ on a : $$ 1 \leqslant u_{n+1} \leqslant u_n \leqslant 4. $$
-
- Soit $x$ un réel de l'intervalle $]-\infty~;~5[$.
Prouver l'équivalence suivante : $$ f(x) = x \iff x^2 - 5x + 4 = 0. $$ - Résoudre $f(x) = x$ dans l'intervalle $]-\infty~;~5[$.
- Soit $x$ un réel de l'intervalle $]-\infty~;~5[$.
- Démontrer que la suite $\left(u_n\right)$ est convergente.
Déterminer sa limite. - Le comportement de la suite serait-il identique en choisissant comme terme initial $u_0 = 4$ au lieu de $u_0 = 3$ ?
Polynesie 20 Juin 2024 Jour 2
1 exercice
On considère la suite $\left(u_n\right) $ définie par :
$ u_0 = 8 $ et pour tout entier naturel $ n $, $$ u_{n+1} = u_n -\ln\left(\frac{u_n}{4}\right). $$
-
- Donner les valeurs arrondies au centième de $ u_1 $ et $ u_2 $.
- On considère la fonction
mysteredéfinie ci-dessous en Python. On admet que, pour tout réel strictement positifa,log(a)renvoie la valeur du logarithme népérien dea.
def mystere(k) :
u = 8
S = 0
for i in range(k) :
S = S + u
u = u - log( u / 4 )
return S
L'exécution de mystere(10) renvoie 58.44045206721732. Que représente ce résultat ?
Modifier la fonction précédente afin qu'elle renvoie la moyenne des $ k $ premiers termes de la suite $ \left(u_n\right) $.
- On considère la fonction $ f $ définie et dérivable sur $ ]0~;~+\infty[ $ par : $$ f(x) = x - \ln\left(\frac{x}{4}\right). $$ Étudier les variations de $ f $ sur $ ]0~;~+\infty[ $ et dresser son tableau de variations.
On précisera la valeur exacte du minimum de $ f $ sur $ ]0~;~+\infty[ $. Les limites ne sont pas demandées.
Dans la suite de l'exercice, on remarquera que pour tout entier naturel $ n $, $$ u_{n+1} = f\left(u_n\right). $$
-
- Démontrer, par récurrence, que pour tout entier naturel $ n $, on a : $$ 1 \leqslant u_{n+1} \leqslant u_n. $$
- En déduire que la suite $ \left(u_n\right) $ converge vers une limite réelle.
- On note $ \ell $ la valeur de cette limite.
- Résoudre l’équation $ f(x) = x $.
- En déduire la valeur de $ \ell $.
Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire