Sujets de Bac
2024
Loi des grands nombres
Filtrer par chapitre
Amerique Du Nord 21 Mai 2024 Jour 1
1 exercice
Un jeu vidéo récompense par un objet tiré au sort les joueurs ayant remporté un défi. L’objet tiré peut être « commun » ou « rare ». Deux types d'objets communs ou rares sont disponibles, des épées et des boucliers.
Les concepteurs du jeu vidéo ont prévu que :
— la probabilité de tirer un objet rare est de 7 % ;
— si on tire un objet rare, la probabilité que ce soit une épée est de 80 % ;
— si on tire un objet commun, la probabilité que ce soit une épée est de 40 %.
Les parties A et B sont indépendantes.
Partie A
Un joueur vient de remporter un défi et tire au sort un objet. On note :
- $R$ l'évènement « le joueur tire un objet rare » ;
- $E$ l'évènement « le joueur tire une épée » ;
- $\overline{R}$ et $\overline{E}$ et les évènements contraires des évènements $R$ et $E$.
- Dresser un arbre pondéré modélisant la situation, puis calculer $P(R \cap E)$.
- Calculer la probabilité de tirer une épée.
- Le joueur a tiré une épée. Déterminer la probabilité que ce soit un objet rare. Arrondir le résultat au millième.
Partie B
Un joueur remporte 30 défis. On note $X$ la variable aléatoire correspondant au nombre d’objets rares que le joueur obtient après avoir remporté 30 défis. Les tirages successifs sont considérés comme indépendants.
- Déterminer, en justifiant, la loi de probabilité suivie par la variable aléatoire $X$. Préciser ses paramètres, ainsi que son espérance.
- Déterminer $P(X < 6)$. Arrondir le résultat au millième.
- Déterminer la plus grande valeur de $k$ telle que $P(X \geq k) \geq 0,5$. Interpréter le résultat dans le contexte de l’exercice.
- Les développeurs du jeu vidéo veulent proposer aux joueurs d’acheter un « ticket d’or » qui permet de tirer $N$ objets. La probabilité de tirer un objet rare reste de 7 %.
Les développeurs aimeraient qu’en achetant un ticket d’or, la probabilité qu’un joueur obtienne au moins un objet rare lors de ces $N$ tirages soit supérieure ou égale à 0,95. Déterminer le nombre minimum d’objets à tirer pour atteindre cet objectif. On veillera à détailler la démarche mise en œuvre.
Metropole 19 Juin 2024 Jour 1
1 exercice
Une agence de marketing a étudié la satisfaction des clients concernant le service clientèle à l'occasion de l'achat d'un téléviseur. Ces achats ont été réalisés soit sur internet, soit dans une chaîne de magasins d'électroménager, soit dans une enseigne de grandes surfaces.
Les achats sur internet représentent $60\%$ des ventes, les achats en magasin d'électroménager $30\%$ des ventes et ceux en grandes surfaces $10\%$ des ventes.
Une enquête montre que la proportion des clients satisfaits du service clientèle est de :
- $75\%$ pour les clients sur internet ;
- $90\%$ pour les clients en magasin d'électroménager ;
- $80\%$ pour les clients en grande surface.
On choisit au hasard un client ayant acheté le modèle de téléviseur concerné.
On définit les évènements suivants :
- $I$ : « le client a effectué son achat sur internet » ;
- $M$ : « le client a effectué son achat en magasin d'électroménager » ;
- $G$ : « le client a effectué son achat en grande surface » ;
- $S$ : « le client est satisfait du service clientèle ».
Si $A$ est un évènement quelconque, on notera $\overline{A}$ son évènement contraire et $P(A)$ sa probabilité.
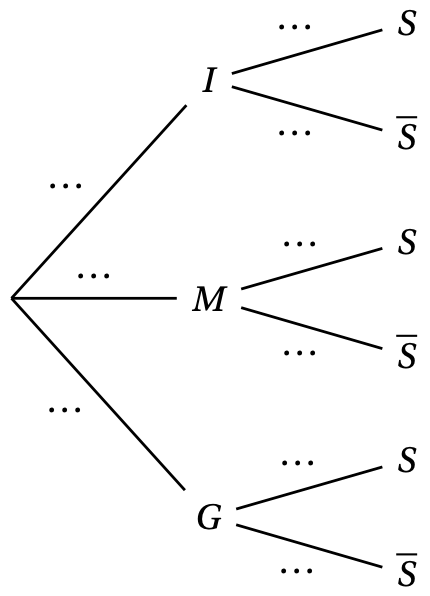
- Reproduire et compléter l'arbre ci-contre.
- Calculer la probabilité que le client ait réalisé son achat sur internet et soit satisfait du service clientèle.
- Démontrer que $P(S) = 0.8$.
- Un client est satisfait du service clientèle. Quelle est la probabilité qu'il ait effectué son achat sur internet ? On donnera un résultat arrondi à $10^{-3}$ près.
-
Pour réaliser l'étude, l'agence doit contacter chaque jour 30 clients parmi les acheteurs du téléviseur. On suppose que le nombre de clients est suffisamment important pour assimiler le choix des 30 clients à un tirage avec remise. On note $X$ la variable aléatoire qui, à chaque échantillon de 30 clients, associe le nombre de clients satisfaits du service clientèle.
- Justifier que $X$ suit une loi binomiale dont on précisera les paramètres.
- Déterminer la probabilité, arrondie à $10^{-3}$ près, qu'au moins 25 clients soient satisfaits dans un échantillon de 30 clients contactés sur une même journée.
- En résolvant une inéquation, déterminer la taille minimale de l'échantillon de clients à contacter pour que la probabilité qu'au moins l'un d'entre eux ne soit pas satisfait soit supérieure à $0.99$.
-
Dans les deux questions a. et b. qui suivent, on ne s'intéresse qu'aux seuls achats sur internet.
Lorsqu'une commande de téléviseur est passée par un client, on considère que le temps de livraison du téléviseur est modélisé par une variable aléatoire $T$ égale à la somme de deux variables aléatoires $T_1$ et $T_2$.La variable aléatoire $T_1$ modélise le nombre entier de jours pour l'acheminement du téléviseur depuis un entrepôt de stockage vers une plateforme de distribution. La variable aléatoire $T_2$ modélise le nombre entier de jours pour l'acheminement du téléviseur depuis cette plateforme jusqu'au domicile du client.
On admet que les variables aléatoires $T_1$ et $T_2$ sont indépendantes, et on donne :
- L'espérance $E(T_1) = 4$ et la variance $V(T_1) = 2$ ;
- L'espérance $E(T_2) = 3$ et la variance $V(T_2) = 1$.
- Déterminer l'espérance $E(T)$ et la variance $V(T)$ de la variable aléatoire $T$.
- Un client passe une commande de téléviseur sur internet. Justifier que la probabilité qu'il reçoive son téléviseur entre 5 et 9 jours après sa commande est supérieure ou égale à $\dfrac{2}{3}$.
Metropole 20 Juin 2024 Jour 2
1 exercice
La directrice d'une école souhaite réaliser une étude auprès des étudiants qui ont passé l'examen de fin d'étude, pour analyser la façon dont ils pensent avoir réussi cet examen.
Pour cette étude, on demande aux étudiants à l'issue de l'examen de répondre individuellement à la question : « Pensez-vous avoir réussi l'examen ? »
Seules les réponses « oui » ou « non » sont possibles, et on observe que $91,7 %$ des étudiants interrogés ont répondu « oui ».
Suite à la publication des résultats à l'examen, on découvre que :
- $65\%$ des étudiants ayant échoué ont répondu « non » ;
- $98\%$ des étudiants ayant réussi ont répondu « oui ».
On interroge au hasard un étudiant qui a passé l'examen.
On note $R$ l'évènement « l'étudiant a réussi l'examen » et $Q$ l'évènement « l'étudiant a répondu « oui » à la question ».
Pour un évènement $A$ quelconque, on note $P(A)$ sa probabilité et $\overline{A}$ son évènement contraire.
Dans tout l'exercice, les probabilités sont, si besoin, arrondies à $10^{-3}$ près.
- Préciser les valeurs des probabilités $P(Q)$ et $P_{\overline{R}}(\overline{Q})$.
-
On note $x$ la probabilité que l'étudiant interrogé ait réussi l'examen.
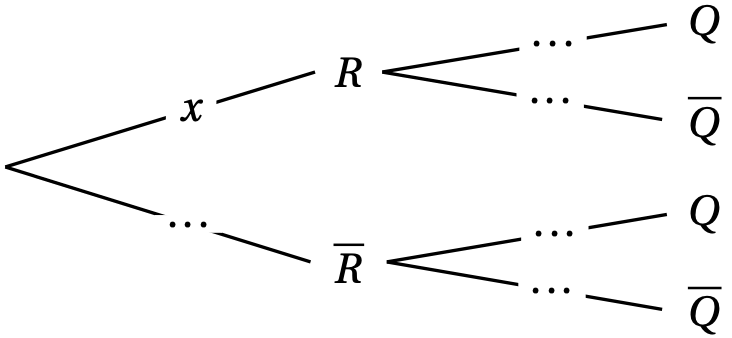
- Recopier et compléter l'arbre pondéré ci-dessous.
- Montrer que $x = 0,9$.
- L'étudiant interrogé a répondu « oui » à la question.
Quelle est la probabilité qu'il ait réussi l'examen ? - La note obtenue par un étudiant interrogé au hasard est un nombre entier entre 0 et 20. On suppose qu'elle est modélisée par une variable aléatoire $N$ qui suit la loi binomiale de paramètres $ (20;~0,615) $.
La directrice souhaite attribuer une récompense aux étudiants ayant obtenu les meilleurs résultats.
À partir de quelle note doit-elle attribuer les récompenses pour que $65%$ des étudiants soient récompensés ? - On interroge au hasard dix étudiants.
Les variables aléatoires $N_1, N_2, \dots, N_{10}$ modélisent la note sur 20 obtenue à l'examen par chacun d'entre eux. On admet que ces variables sont indépendantes et suivent la même loi binomiale de paramètres $ (20;~0,615) $.
Soit $S$ la variable définie par : $$ S = N_1 + N_2 + \dots + N_{10}. $$ Calculer l'espérance $E(S)$ et la variance $V(S)$ de la variable aléatoire $S$. -
On considère la variable aléatoire $M = \dfrac{S}{10}$.
- Que modélise cette variable aléatoire $M$ dans le contexte de l'exercice ?
- Justifier que $E(M) = 12,3$ et $V(M) = 0,47355$.
- À l'aide de l'inégalité de Bienaymé-Tchebychev, justifier l'affirmation suivante :
« La probabilité que la moyenne des notes de dix étudiants pris au hasard soit strictement comprise entre 10,3 et 14,3 est d'au moins $80\%$. »
Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire