Terminale Spécialité

Cet exercice est un questionnaire à choix multiple.
Pour chaque question, une seule des quatre réponses proposées est exacte.
Le candidat indiquera sur sa copie le numéro de la question et la réponse choisie.
Aucune justification n’est demandée.
Une réponse fausse, une réponse multiple ou l’absence de réponse à une question ne rapporte ni n’enlève de point.
Les quatre questions sont indépendantes.

L’espace est rapporté à un repère orthonormé $ ( O ; \overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k} ) $.

1. On considère les points $ A(1; 0; 3) $ et $ B(4; 1; 0) $.
   Une représentation paramétrique de la droite (AB) est :
   1. $ \left\{ \begin{array}{l} x = 3 + t \\ y = 1 \\ z = -3 + 3t \end{array} \right. \quad \text{avec } t \in \mathbb{R} $
   2. $ \left\{ \begin{array}{l} x = 1 + 4t \\ y = t \\ z = 3 \end{array} \right. \quad \text{avec } t \in \mathbb{R} $
   3. $ \left\{ \begin{array}{l} x = 1 + 3t \\ y = t \\ z = 3 - 3t \end{array} \right. \quad \text{avec } t \in \mathbb{R} $
   4. $ \left\{ \begin{array}{l} x = 4 + t \\ y = 1 \\ z = 3 - 3t \end{array} \right. \quad \text{avec } t \in \mathbb{R} $
2. On considère la droite $(d)$ de représentation paramétrique $$ \left\{ \begin{array}{l} x = 3 + 4t \\ y = 6t \\ z = 4 - 2t \end{array} \right. \quad \text{avec } t \in \mathbb{R} $$
   Parmi les points suivants, lequel appartient à la droite $(d)$ ?
   1. $M(7;~6;~6)$
   2. $N(3;~6;~4)$
   3. $P(4;~6;~-2)$
   4. $R(-3;~-9;~7)$
3. On considère la droite $(d')$ de représentation paramétrique $$ \left\{ \begin{array}{l} x = -2 + 3k \\ y = -1 - 2k \\ z = 1 + k \end{array} \right. \quad \text{avec } k \in \mathbb{R} $$
   Les droites $(d)$ et $(d')$ sont :
   1. sécantes
   2. non coplanaires
   3. parallèles
   4. confondues
4. On considère le plan $(P)$ passant par le point $I(2;~1;~0)$ et perpendiculaire à la droite $(d)$.
   Une équation du plan $(P)$ est :
   1. $2x + 3y - z - 7 = 0$
   2. $-x + y - 4z + 1 = 0$
   3. $4x + 6y - 2z + 9 = 0$
   4. $2x + y + 1 = 0$

On considère le pavé droit ABCDEFGH tel que $ AB = 3 $ et $ AD = AE = 1 $ représenté ci-dessous.

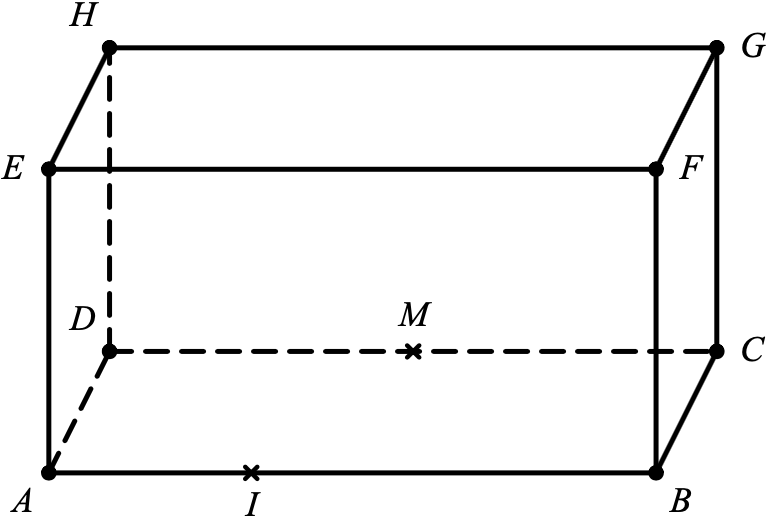
On considère le point I du segment $ [AB] $ tel que $ \overrightarrow{AB} = 3\overrightarrow{AI} $ et on appelle M le milieu du segment $ [CD] $.
On se place dans le repère orthonormé $ ( A ; \overrightarrow{AI}, \overrightarrow{AD}, \overrightarrow{AE} ) $.

1. Sans justifier, donner les coordonnées des points F, H et M.
2. 1. Montrer que le vecteur $ \overrightarrow{n} \begin{pmatrix} 2 \\ 6 \\ 3 \end{pmatrix} $ est un vecteur normal au plan (HMF).
   2. En déduire qu’une équation cartésienne du plan (HMF) est : $$ 2x + 6y + 3z - 9 = 0. $$
   3. Le plan $ \mathcal{P} $ dont une équation cartésienne est $ 5x + 15y - 3z + 7 = 0 $ est-il parallèle au plan (HMF) ? Justifier la réponse.
3. Déterminer une représentation paramétrique de la droite (DG).
4. On appelle N le point d’intersection de la droite (DG) avec le plan (HMF). Déterminer les coordonnées du point N.
5. Le point R de coordonnées $ \left( 3; \frac{1}{4}; \frac{1}{2} \right) $ est-il le projeté orthogonal du point G sur le plan (HMF) ? Justifier la réponse.

1. Dans l’espace muni d’un repère orthonormé $ ( O ; \overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k} ) $ d’unité 1 cm, on considère les points :

   $ A(3 ; -1 ; 1) $, $ B(4 ; -1 ; 0) $, $ C(0 ; 3 ; 2) $, $ D(4 ; 3 ; -2) $ et $ S(2 ; 1 ; 4) $.

   Dans cet exercice on souhaite montrer que $ SABDC $ est une pyramide à base $ ABDC $ trapézoïdale de sommet $ S $, afin de calculer son volume.

2. 

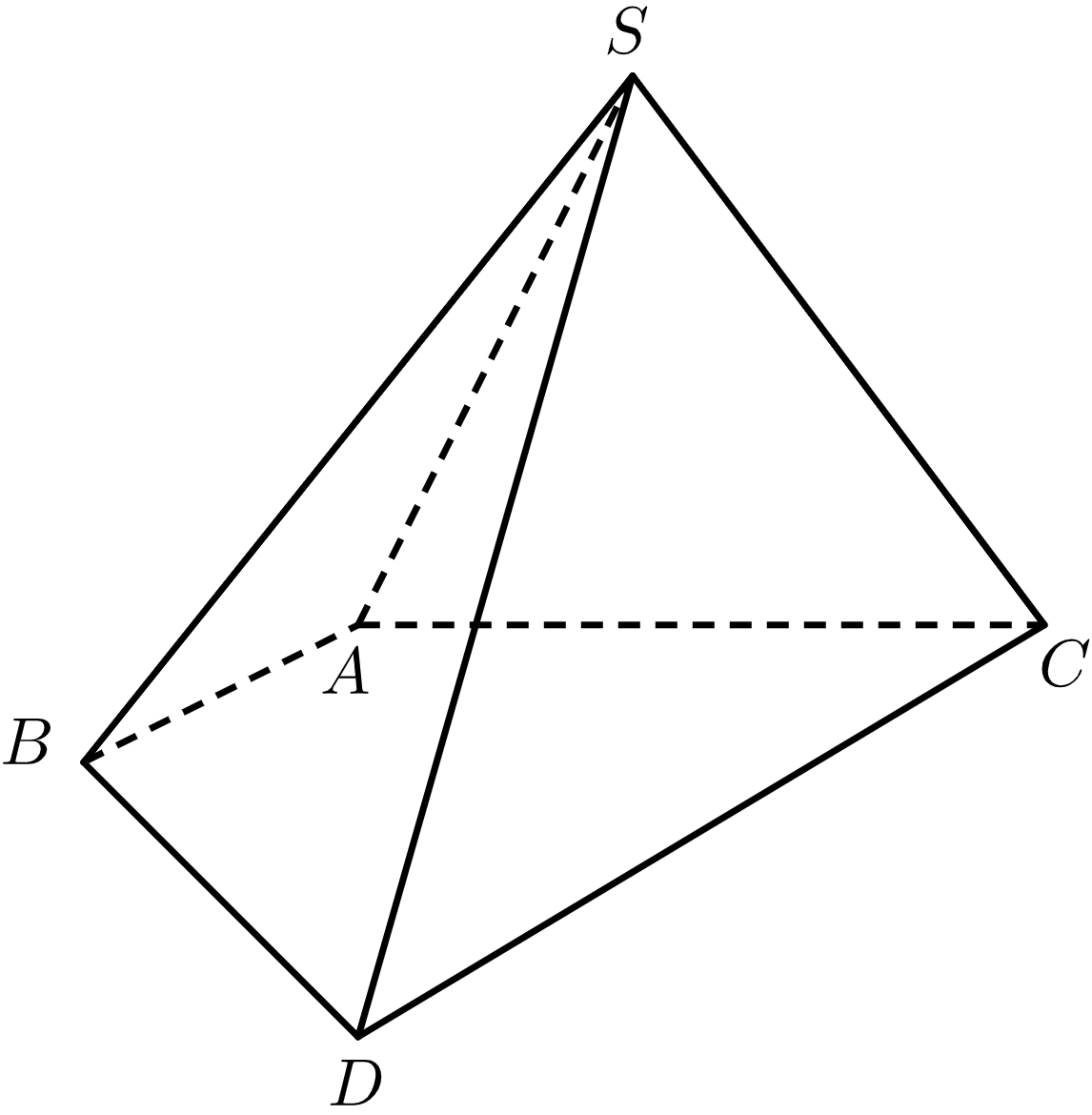
1. Montrer que les points $ A $, $ B $ et $ C $ ne sont pas alignés.
2. 1. Montrer que les points $ A $, $ B $, $ C $ et $ D $ sont coplanaires.
   2. Montrer que le quadrilatère $ ABDC $ est un trapèze de bases $ [AB] $ et $ [CD] $.
      On rappelle qu’un trapèze est un quadrilatère ayant deux côtés opposés parallèles appelés bases.
3. 1. Démontrer que le vecteur $ \overrightarrow{n} (2 ; 1 ; 2) $ est un vecteur normal au plan $(ABC)$.
   2. En déduire une équation cartésienne du plan $(ABC)$.
   3. Déterminer une représentation paramétrique de la droite $ \Delta $ passant par le point $ S $ et orthogonale au plan $(ABC)$.
   4. On note $ I $ le point d’intersection de la droite $ \Delta $ et du plan $(ABC)$.
      Montrer que le point $ I $ a pour coordonnées $ \Big( \dfrac{2}{3} ;~\dfrac{1}{3} ;~\dfrac{8}{3} \Big) $, puis montrer que $ SI = 2 $ cm.
4. 1. Vérifier que le projeté orthogonal $ H $ du point $ B $ sur la droite $(CD)$ a pour coordonnées $ H(3 ; 3 ; -1) $ et montrer que $ HB = 3 \sqrt{2} $ cm.
   2. Calculer la valeur exacte de l’aire du trapèze $ ABDC $.
      On rappelle que l’aire d’un trapèze est donnée par la formule$ $$\mathcal{A} = \dfrac{b + B}{2} \times h $$ où $ b $ et $ B $ sont les longueurs des bases du trapèze et $ h $ sa hauteur.
5. Déterminer le volume de la pyramide $ SABDC $.
   On rappelle que le volume $ V $ d’une pyramide est donné par la formule $$ V = \frac{1}{3} \times \text{aire de la base} \times \text{hauteur} $$.

1. Dans un repère orthonormé $ ( \left( O ; \overrightarrow{i} , \overrightarrow{j} , \overrightarrow{k} \right) ) $ de l'espace, on considère le plan $ (P) $ d'équation :

   $$ (P) : \quad 2x + 2y - 3z + 1 = 0. $$

   On considère les trois points A, B et C de coordonnées :

   • $ A(1 ; 0 ; 1) $
   • $ B(2 ; -1 ; 1) $
   • et $ C(-4 ; -6 ; 5) $

   Le but de cet exercice est d’étudier le rapport des aires entre un triangle et son projeté orthogonal dans un plan.

2. 

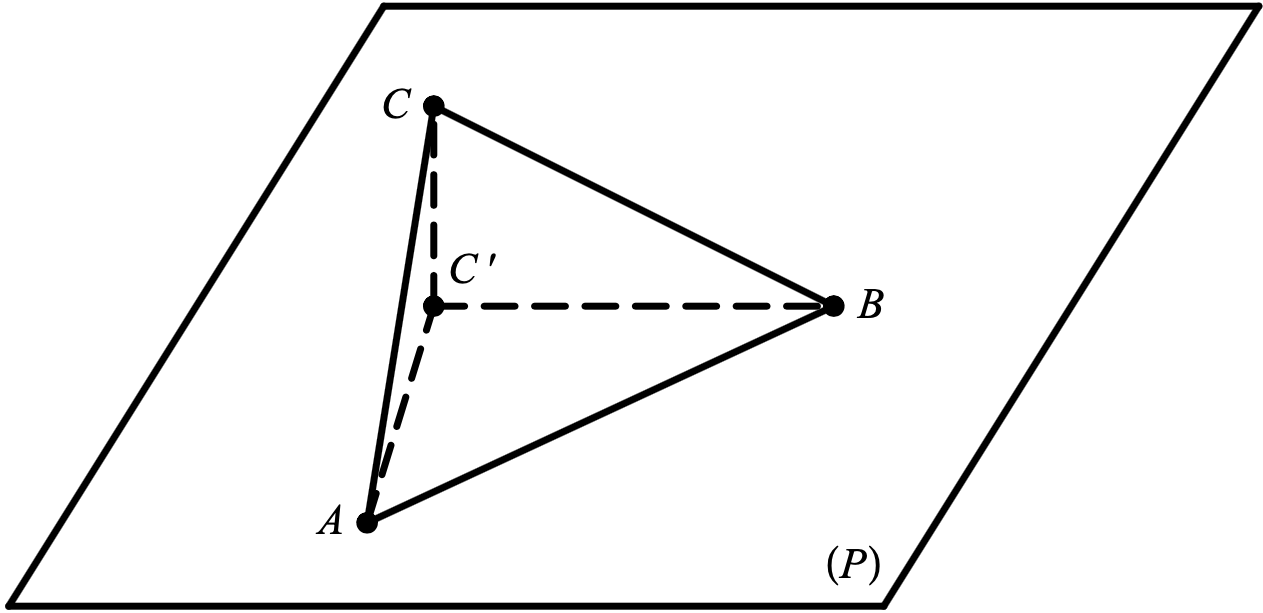
Partie A

1. Pour chacun des points A, B et C, vérifier s’il appartient au plan $ (P) $.
2. Montrer que le point $ C'(0 ; -2 ; -1) $ est le projeté orthogonal du point C sur le plan $ (P) $.
3. Déterminer une représentation paramétrique de la droite $ (AB) $.
4. On admet l’existence d’un unique point H vérifiant les deux conditions $$ \begin{cases} H \in (AB) \\ (AB) \text{ et } (HC) \text{ sont orthogonales.} \end{cases} $$

   Déterminer les coordonnées du point H.

Partie B

On admet que les coordonnées du vecteur $ \overrightarrow{HC} $ sont :

$$ \overrightarrow{HC} \begin{pmatrix} -\dfrac{11}{2} \\ -\dfrac{11}{2} \\ 4 \end{pmatrix} $$

1. Calculer la valeur exacte de $ \| \overrightarrow{HC} \| $.
2. Soit S l’aire du triangle ABC. Déterminer la valeur exacte de S.

Partie C

On admet que $ HC' = \dfrac{\sqrt{17}}{2} $.

1. Soit $ \alpha = \widehat{CHC'} $. Déterminer la valeur de $ \cos(\alpha) $.
2. 1. Montrer que les droites $ (C'H) $ et $ (AB) $ sont perpendiculaires.
   2. Calculer S’ l’aire du triangle ABC’, on donnera la valeur exacte.
   3. Donner une relation entre S, S’ et $ \cos(\alpha) $.

L’espace est muni d’un repère orthonormé $ ( O ; \overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k} ) $.
On considère :

• les points $ A(-2 ; 0 ; 2) $, $ B(-1 ; 3 ; 0) $, $ C(1 ; -1 ; 2) $ et $ D(0 ; 0 ; 3) $.
• la droite $ \mathcal{D}_1 $ dont une représentation paramétrique est : $$ \left\{ \begin{array}{l} x = t \\ y = 3t \\ z = 3 + 5t \end{array} \right. \quad \text{avec } t \in \mathbb{R}. $$
• la droite $ \mathcal{D}_2 $ dont une représentation paramétrique est : $$ \left\{ \begin{array}{l} x = 1 + 3s \\ y = -1 - 5s \\ z = 2 - 6s \end{array} \right. \quad \text{avec } s \in \mathbb{R}. $$

1. Démontrer que les points $ A $, $ B $ et $ C $ ne sont pas alignés.
2. 1. Démontrer que le vecteur $ \overrightarrow{n} \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix} $ est orthogonal au plan (ABC).
   2. Justifier qu’une équation cartésienne du plan (ABC) est : $$ x + 3y + 5z - 8 = 0. $$
   3. En déduire que les points $ A $, $ B $, $ C $ et $ D $ ne sont pas coplanaires.
3. 1. Justifier que la droite $ \mathcal{D}_1 $ est la hauteur du tétraèdre $ ABCD $ issue de $ D $.
      On admet que la droite $ \mathcal{D}_2 $ est la hauteur du tétraèdre $ ABCD $ issue de $ C $.
   2. Démontrer que les droites $ \mathcal{D}_1 $ et $ \mathcal{D}_2 $ sont sécantes et déterminer les coordonnées de leur point d’intersection.
4. 1. Déterminer les coordonnées du projeté orthogonal $ H $ du point $ D $ sur le plan (ABC).
   2. Calculer la distance du point $ D $ au plan (ABC).
      Arrondir le résultat au centième.

Le cube $ ABCDEFGH $ a pour arête 1 cm.
Le point $ I $ est le milieu du segment $ [AB] $ et le point $ J $ est le milieu du segment $ [CG] $.

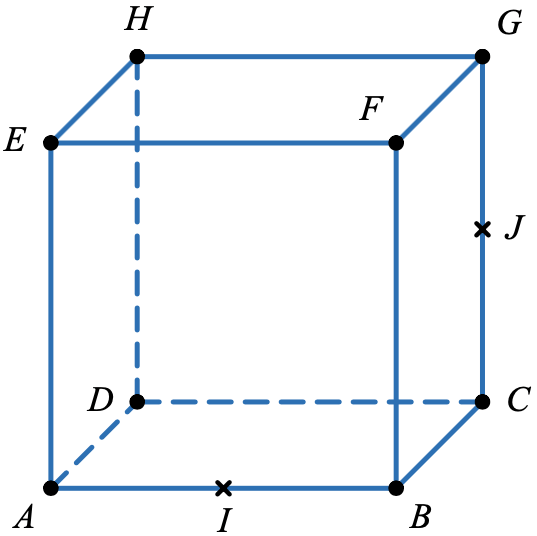
On se place dans le repère orthonormé $ ( A ; \overrightarrow{AB}, \overrightarrow{AD}, \overrightarrow{AE} ) $.

1. Donner les coordonnées des points $ I $ et $ J $.
2. Montrer que le vecteur $ \overrightarrow{EJ} $ est normal au plan $(FHI)$.
3. Montrer qu’une équation cartésienne du plan $(FHI)$ est : $$ -2x - 2y + z + 1 = 0. $$
4. Déterminer une représentation paramétrique de la droite $(EJ)$.
5. 1. On note $ K $ le projeté orthogonal du point $ E $ sur le plan $(FHI)$. Calculer ses coordonnées.
   2. Montrer que le volume de la pyramide $ EFHI $ est $ \frac{1}{6} $ cm$ ^3 $.

      On pourra utiliser le point $ L $, milieu du segment $ [EF] $. On admet que ce point est le projeté orthogonal du point $ I $ sur le plan $(EFH)$.

   3. Déduire des deux questions précédentes l’aire du triangle $FHI$.