Sujets de Bac
2024
Fonctions logarithmes
Filtrer par chapitre
Amerique Du Nord 21 Mai 2024 Jour 1
1 exercice
Le but de cet exercice est d’étudier la fonction $ f $ définie sur l’intervalle $ ]0 ; +\infty[ $ par: $$f(x) = x\ln(x^2) - \frac{1}{x}$$
Partie A : lectures graphiques
On a tracé ci-dessous la courbe représentative $(\mathcal{C}_f)$ de la fonction $ f $, ainsi que la droite $(T)$, tangente à la courbe $(\mathcal{C}_f)$ au point $A(1;~-1)$.
Cette tangente passe également par le point $B(0;~-4)$.
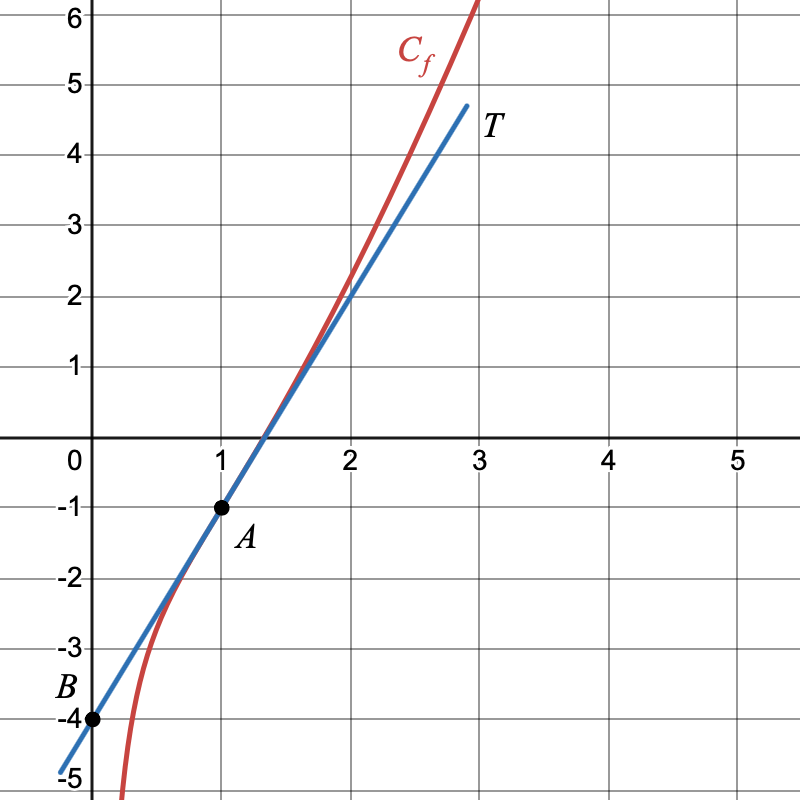
- Lire graphiquement $f'(1)$ et donner l’équation réduite de la tangente $(T)$.
- Donner les intervalles sur lesquels la fonction $ f $ semble convexe ou concave. Que semble représenter le point A pour la courbe $(\mathcal{C}_f)$ ?
Partie B : étude analytique
- Déterminer, en justifiant, la limite de $ f $ en $+\infty$, puis sa limite en 0.
- On admet que la fonction $ f $ est deux fois dérivable sur l’intervalle $ ]0 ; +\infty[ $.
- Déterminer $ f'(x) $ pour $ x $ appartenant à l’intervalle $ ]0 ; +\infty[ $.
- Montrer que pour tout $ x $ appartenant à l’intervalle $ ]0 ; +\infty[ $, $$f''(x) = \frac{2(x+1)(x-1)}{x^3}$$
-
- Étudier la convexité de la fonction $ f $ sur l’intervalle $ ]0 ; +\infty[ $.
- Étudier les variations de la fonction $ f' $, puis le signe de $ f'(x) $ pour $ x $ appartenant à l’intervalle $ ]0 ; +\infty[ $.
En déduire le sens de variation de la fonction $ f $ sur l’intervalle $ ]0 ; +\infty[ $.
-
- Montrer que l’équation $ f(x) = 0 $ admet une unique solution $ \alpha $ sur l’intervalle $ ]0 ; +\infty[ $.
- Donner la valeur arrondie au centième de $ \alpha $ et montrer que $ \alpha $ vérifie : $$\alpha^2 = \exp\left( \frac{1}{\alpha^2} \right)$$
Amerique Du Nord 22 Mai 2024 Jour 2
2 exercices
On considère la fonction $ g $ définie sur l’intervalle $ [0 ; 1] $ par : $$ g(x) = 2x - x^2. $$
- Montrer que la fonction $ g $ est strictement croissante sur l’intervalle $ [0 ; 1] $ et préciser les valeurs de $ g(0) $ et de $ g(1) $.
- On considère la suite $ (u_n) $ définie par
$$
\begin{cases}
u_0 = \frac{1}{2} \\
u_{n+1} = g(u_n)
\end{cases}
$$ pour tout entier naturel $ n $.
- Calculer $ u_1 $ et $ u_2 $.
- Démontrer par récurrence que, pour tout entier naturel $ n $, on a : $ 0 < u_n < u_{n+1} < 1 $.
- En déduire que la suite $ (u_n) $ est convergente.
- Déterminer la limite $ \ell $ de la suite $ (u_n) $.
- On considère la suite $ (v_n) $ définie pour tout entier naturel $ n $ par $ v_n = \ln(1 - u_n) $.
- Démontrer que la suite $ (v_n) $ est une suite géométrique de raison 2 et préciser son premier terme.
- En déduire une expression de $ v_n $ en fonction de $ n $.
- En déduire une expression de $ u_n $ en fonction de $ n $ et retrouver la limite déterminée à la question 5.
- Recopier et compléter le script Python ci-dessous afin que celui-ci renvoie le rang $ n $ à partir duquel la suite dépasse 0,95.
Soit $ a $ un réel strictement positif.
On considère la fonction $ f $ définie sur l’intervalle $ ]0 ; +\infty[ $ par :
$$f(x) = a\ln(x).$$
On note $C_f$ sa courbe représentative dans un repère orthonormé.
Soit $ x_0 $ un réel strictement supérieur à 1.
- Déterminer l’abscisse du point d’intersection de la courbe $C_f$ et de l’axe des abscisses.
- Vérifier que la fonction $ F $ définie par $ F(x) = a[x\ln(x) - x] $ est une primitive de la fonction $ f $ sur l’intervalle $ ]0 ; +\infty[ $.
- En déduire l’aire du domaine bleuté en fonction de $ a $ et de $ x_0 $.
- Démontrer que la longueur $ AB $ est égale à une constante (c’est-à-dire à un nombre qui ne dépend pas de $ x_0 $) que l’on déterminera.
Le candidat prendra soin d’expliciter sa démarche.
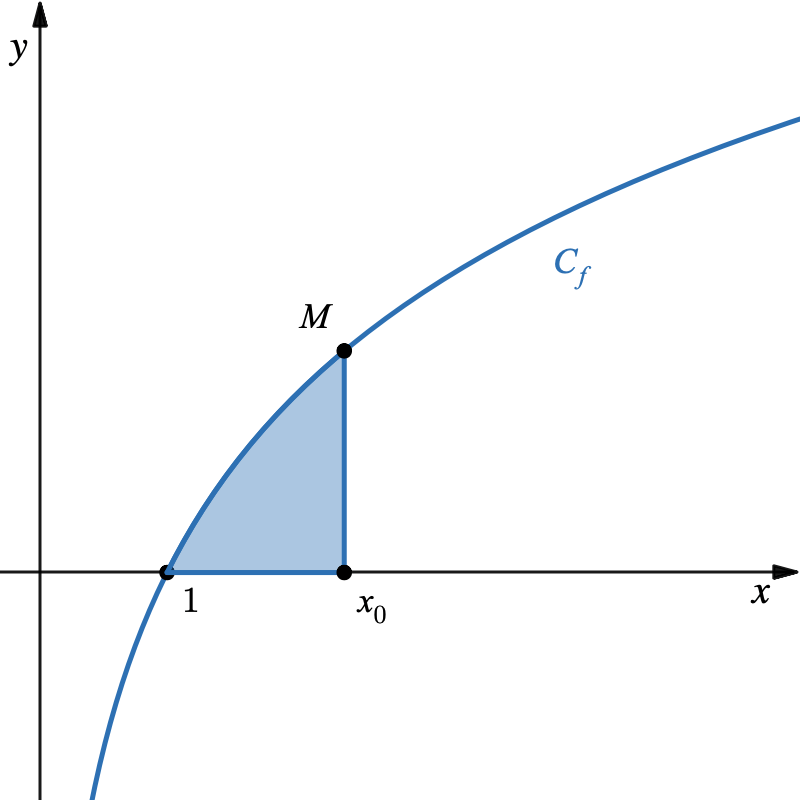
On note $ T $ la tangente à la courbe $C_f$ au point $ M $ d’abscisse $ x_0 $.
On appelle $ A $ le point d’intersection de la tangente $ T $ avec l’axe des ordonnées et $ B $ le projeté orthogonal de $ M $ sur l’axe des ordonnées.
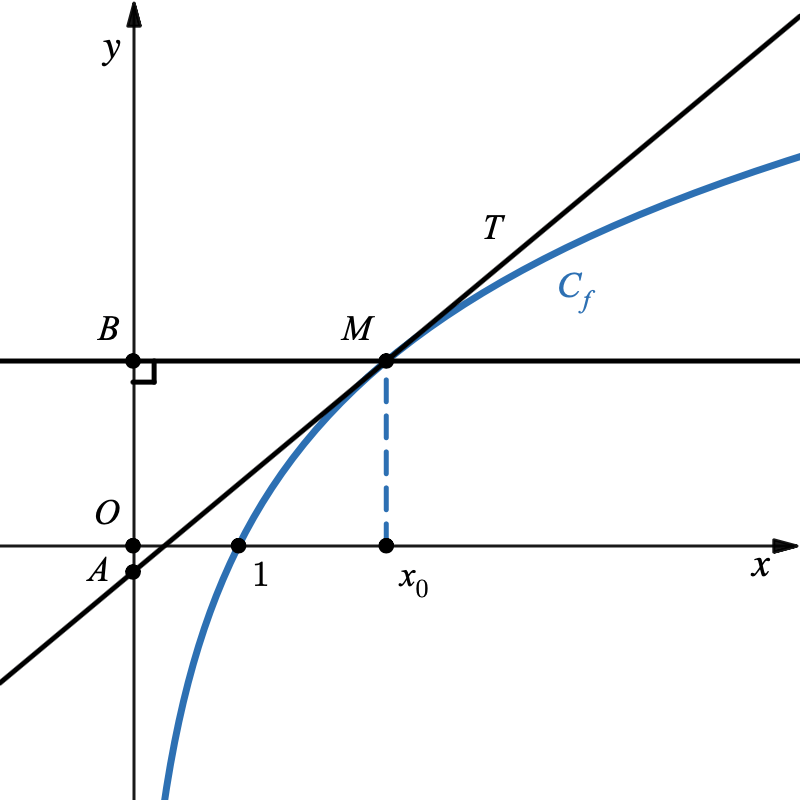
Asie 11 Juin 2024 Jour 2
1 exercice
On considère la fonction $ f $ définie sur $ ]0 ; +\infty[ $ par :
$$
f(x) = x^2 - x\ln(x).
$$
On admet que $ f $ est deux fois dérivable sur $ ]0 ; +\infty[ $.
On note $ f' $ la fonction dérivée de la fonction $ f $ et $ f'' $ la fonction dérivée de la fonction $ f' $.
Partie A : Étude de la fonction $ f $
- Déterminer les limites de la fonction $ f $ en 0 et en $ +\infty $.
- Pour tout réel $ x $ strictement positif, calculer $ f'(x) $.
- Montrer que pour tout réel $ x $ strictement positif : $$ f''(x) = \frac{2x - 1}{x}. $$
- Étudier les variations de la fonction $ f' $ sur $ ]0 ; +\infty[ $, puis dresser le tableau des variations de la fonction $ f' $ sur $ ]0 ; +\infty[ $.
On veillera à faire apparaître la valeur exacte de l’extrémum de la fonction $ f' $ sur $ ]0 ; +\infty[ $.
Les limites de la fonction $ f' $ aux bornes de l’intervalle de définition ne sont pas attendues. - Montrer que la fonction $ f $ est strictement croissante sur $ ]0 ; +\infty[ $.
Partie B : Étude d’une fonction auxiliaire pour la résolution de l’équation $ f(x) = x $
On considère dans cette partie la fonction $ g $ définie sur $ ]0 ; +\infty[ $ par :
$$
g(x) = x - \ln(x).
$$
On admet que la fonction $ g $ est dérivable sur $ ]0 ; +\infty[ $, on note $ g' $ sa dérivée.
- Pour tout réel strictement positif, calculer $ g'(x) $, puis dresser le tableau des variations de la fonction $ g $.
Les limites de la fonction $ g $ aux bornes de l’intervalle de définition ne sont pas attendues. - On admet que 1 est l’unique solution de l’équation $ g(x) = 1 $.
Résoudre, sur l’intervalle $ ]0 ; +\infty[ $, l’équation $ f(x) = x $.
Partie C : Étude d’une suite récurrente
On considère la suite $ (u_n) $ définie par $ u_0 = \frac{1}{2} $ et pour tout entier naturel $ n $, $$ u_{n+1} = f(u_n) = u_n^2 - u_n\ln(u_n). $$
- Montrer par récurrence que pour tout entier naturel $ n $ : $$ \frac{1}{2} \leq u_n \leq u_{n+1} \leq 1. $$
- Justifier que la suite $ (u_n) $ converge.
On appelle $ \ell $ la limite de la suite $ (u_n) $ et on admet que $ \ell $ vérifie l’égalité $ f(\ell) = \ell $. - Déterminer la valeur de $ \ell $.
Metropole 19 Juin 2024 Jour 1
1 exercice
Partie A : étude de la fonction $f$
La fonction $f$ est définie sur l'intervalle $]0 ~;~+\infty[$ par :
$f(x) = x - 2 + \dfrac{1}{2} \ln x,$
où $\ln$ désigne la fonction logarithme népérien. On admet que la fonction $f$ est deux fois dérivable sur $]0 ~;~ +\infty[$. On note $f'$ sa dérivée et $f''$ sa dérivée seconde.
-
- Déterminer, en justifiant, les limites de $f$ en 0 et en $+\infty$.
- Montrer que pour tout $x$ appartenant à $]0 ~;~+\infty[$, on a : $f'(x) = \dfrac{2x + 1}{2x}$.
- Étudier le sens de variation de $f$ sur $]0 ~;~+\infty[$.
- Étudier la convexité de $f$ sur $]0 ~;~+\infty[$.
-
- Montrer que l'équation $f(x) = 0$ admet dans $]0 ~;~+\infty[$ une solution unique qu'on notera $\alpha$ et justifier que $\alpha$ appartient à l'intervalle $[1~;~2]$.
- Déterminer le signe de $f(x)$ pour $x \in ]0 ~;~+\infty[$.
- Montrer que $\ln(\alpha) = 2(2-\alpha)$.
Partie B : étude de la fonction $g$
La fonction $g$ est définie sur $]0~;~1]$ par :
$g(x) = -\dfrac{7}{8}x^{2} + x - \dfrac{1}{4}x^{2}\ln x.$
On admet que la fonction $g$ est dérivable sur $]0~;~1]$ et on note $g'$ sa fonction dérivée.
- Calculer $g'(x)$ pour $x \in ]0~;~1]$ puis vérifier que $g'(x) = x f\left(\dfrac{1}{x}\right)$.
-
- Justifier que pour $x$ appartenant à l'intervalle $\left]0~;~\dfrac{1}{\alpha}\right[$, on a $f\left(\dfrac{1}{x}\right) > 0$.
- On admet le tableau de signes suivant :
En déduire le tableau de variations de $g$ sur l'intervalle $]0~;~1]$. Les images et les limites ne sont pas demandées.
Partie C : un calcul d'aire
On a représenté sur le graphique ci-dessous :
- La courbe $\mathcal{C}_{g}$ de la fonction $g$ ;
- La parabole $\mathcal{P}$ d'équation $y = -\dfrac{7}{8}x^{2} + x$ sur l'intervalle $]0~;~1]$.
On souhaite calculer l'aire $\mathcal{A}$ du domaine hachuré compris entre les courbes $\mathcal{C}_{g}$ et $\mathcal{P}$, et les droites d'équations $x = \dfrac{1}{\alpha}$ et $x = 1$.
On rappelle que $\ln(\alpha) = 2(2-\alpha)$.
-
- Justifier la position relative des courbes $\mathcal{C}_{g}$ et $\mathcal{P}$ sur l'intervalle $\left]0~;~1\right]$.
- Démontrer l'égalité :
$$ \int_{\frac{1}{\alpha}}^{1} x^{2} \ln x \,\mathrm{d}x = \dfrac{-\alpha^{3} - 6\alpha + 13}{9\alpha^{3}}. $$
- En déduire l'expression en fonction de $\alpha$ de l'aire $\mathcal{A}$.
Metropole 20 Juin 2024 Jour 2
1 exercice
On considère une fonction $f$ définie et deux fois dérivable sur $]-2 ~;~+\infty[$. On note $ \mathcal{C}_{f} $ sa courbe représentative dans un repère orthogonal du plan, $f'$ sa dérivée et $f''$ sa dérivée seconde.
On a tracé ci-dessous la courbe $ \mathcal{C}_{f} $ et sa tangente $T$ au point $B$ d'abscisse $-1$.
On précise que la droite $T$ passe par le point $A(0 ~;~ -1)$.
Partie A : exploitation du graphique.
À l'aide du graphique, répondre aux questions ci-dessous.
- Préciser $f(-1)$ et $f'(-1)$.
- La fonction $f$ est-elle convexe sur son ensemble de définition ? Justifier.
- Conjecturer le nombre de solutions de l'équation $f(x) = 0$ et donner une valeur arrondie à $10^{-1}$ près d'une solution.
Partie B : étude de la fonction $f$
On considère que la fonction $f$ est définie sur $]-2 ~;~+\infty[$ par :
$$ f(x) = x^{2}+ 2x - 1 + \ln (x + 2), $$
où $\ln$ désigne la fonction logarithme népérien.
- Déterminer par le calcul la limite de la fonction $f$ en $-2$. Interpréter graphiquement ce résultat.
On admet que $\lim\limits_{x \to +\infty} f(x)=+\infty$. - Montrer que pour tout $x>-2, \quad f'(x)=\dfrac{2 x^{2}+6 x+5}{x+2}$.
- Étudier les variations de la fonction $f$ sur $]-2 ~;~+\infty[$ puis dresser son tableau de variations complet.
- Montrer que l'équation $f(x)=0$ admet une unique solution $\alpha$ sur $]-2 ~;~+\infty[$ et donner une valeur arrondie de $\alpha$ à $10^{-2}$ près.
- En déduire le signe de $f(x)$ sur $]-2~;~ +\infty[$.
- Montrer que $\mathcal{C}_{f}$ admet un unique point d'inflexion et déterminer son abscisse.
Partie C : une distance minimale.
Soit $g$ la fonction définie sur $]-2 ~;~ +\infty[$ par $~g(x)=\ln (x+2)$.
On note $\mathcal{C}_{g}$ sa courbe représentative dans un repère orthonormé $(\mathrm{0} ~;~ \mathrm{I}~,~ \mathrm{J})$.
Soit $M$ un point de $\mathcal{C}_{g}$ d'abscisse $x$.
Le but de cette partie est de déterminer pour quelle valeur de $x$ la distance $\mathrm{J}M$ est minimale.
On considère la fonction $h$ définie sur $]-2 ~;~ +\infty[$ par $~h(x)=\mathrm{J}M^{2}$.
- Justifier que pour tout $x>-2$, on a :$~~h(x)=x^{2}+[\ln (x+2)-1]^{2}.$
-
- On admet que la fonction $h$ est dérivable sur $]-2 ~;~ +\infty[$ et on note $h'$ sa fonction dérivée.
- On admet également que pour tout réel $x>-2$, $$ h'(x)=\dfrac{2 f(x)}{x+2} $$ où $f$ est la fonction étudiée en partie B.
- Dresser le tableau de variations de $h$ sur $]-2 ~;~ +\infty[$.
Les limites ne sont pas demandées. - En déduire que la valeur de $x$ pour laquelle la distance $\mathrm{J}M$ est minimale est $\alpha$ où $\alpha$ est le nombre réel défini à la question 4. de la partie B.
-
- On notera $M_{\alpha}$ le point de $\mathcal{C}_{g}$ d'abscisse $\alpha$.
- Montrer que $~\ln (\alpha+2)=1-2 \alpha-\alpha^{2}.$
- En déduire que la tangente à $\mathcal{C}_{g}$ au point $M_{\alpha}$ et la droite $(\mathrm{J}M_{\alpha})$ sont perpendiculaires.
- On pourra utiliser le fait que, dans un repère orthonormé, deux droites sont perpendiculaires lorsque le produit de leurs coefficients directeurs est égal à $-1$.
Polynesie 20 Juin 2024 Jour 2
1 exercice
On considère la suite $\left(u_n\right) $ définie par :
$ u_0 = 8 $ et pour tout entier naturel $ n $, $$ u_{n+1} = u_n -\ln\left(\frac{u_n}{4}\right). $$
-
- Donner les valeurs arrondies au centième de $ u_1 $ et $ u_2 $.
- On considère la fonction
mysteredéfinie ci-dessous en Python. On admet que, pour tout réel strictement positifa,log(a)renvoie la valeur du logarithme népérien dea.
def mystere(k) :
u = 8
S = 0
for i in range(k) :
S = S + u
u = u - log( u / 4 )
return S
L'exécution de mystere(10) renvoie 58.44045206721732. Que représente ce résultat ?
Modifier la fonction précédente afin qu'elle renvoie la moyenne des $ k $ premiers termes de la suite $ \left(u_n\right) $.
- On considère la fonction $ f $ définie et dérivable sur $ ]0~;~+\infty[ $ par : $$ f(x) = x - \ln\left(\frac{x}{4}\right). $$ Étudier les variations de $ f $ sur $ ]0~;~+\infty[ $ et dresser son tableau de variations.
On précisera la valeur exacte du minimum de $ f $ sur $ ]0~;~+\infty[ $. Les limites ne sont pas demandées.
Dans la suite de l'exercice, on remarquera que pour tout entier naturel $ n $, $$ u_{n+1} = f\left(u_n\right). $$
-
- Démontrer, par récurrence, que pour tout entier naturel $ n $, on a : $$ 1 \leqslant u_{n+1} \leqslant u_n. $$
- En déduire que la suite $ \left(u_n\right) $ converge vers une limite réelle.
- On note $ \ell $ la valeur de cette limite.
- Résoudre l’équation $ f(x) = x $.
- En déduire la valeur de $ \ell $.
Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire