Terminale Spécialité

Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. Chaque réponse doit être justifiée. Une réponse non justifiée ne rapporte aucun point.

1. Soit $ (u_n) $ une suite définie pour tout entier naturel $ n $ et vérifiant la relation suivante :

   $$ \dfrac{1}{2} < u_n \leq \dfrac{3n^2 + 4n + 7}{6n^2 + 1} \text{ pour tout entier naturel } n $$.

   Affirmation 1 : $ \lim\limits_{n \to +\infty} u_n = \dfrac{1}{2} $.

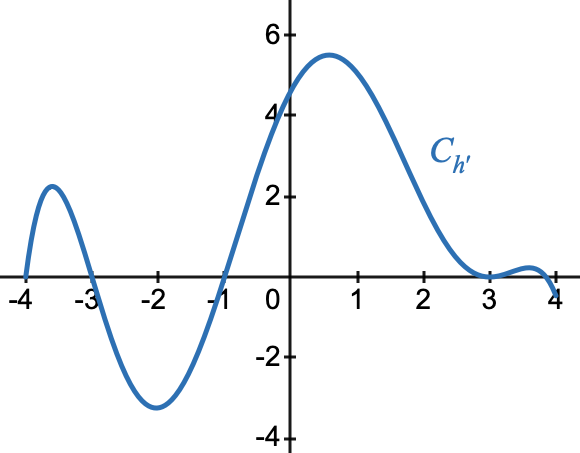
2. Soit $ h $ une fonction définie et dérivable sur l’intervalle $[-4 ; 4]$. La représentation graphique $ \mathcal{C}_{h'} $ de sa fonction dérivée $ h' $ est donnée ci-dessous.

   Affirmation 2 : La fonction $ h $ est convexe sur $[-1 ; 3]$.



3. Le code d’un immeuble est composé de 4 chiffres (qui peuvent être identiques) suivis de deux lettres distinctes parmi A, B et C (exemple : 1232BA).

   Affirmation 3 : Il existe 20 634 codes qui contiennent au moins un 0.

4. On considère la fonction $ f $ définie sur $ \left] 0 ; +\infty \right[ $ par $ f(x) = x \ln x $.

   Affirmation 4 : La fonction $ f $ est une solution sur $ \left] 0 ; +\infty \right[ $ de l’équation différentielle

   $$ x y' - y = x $$.

Un sac opaque contient huit jetons numérotés de 1 à 8, indiscernables au toucher.
À trois reprises, un joueur pioche un jeton dans ce sac, note son numéro, puis le remet dans le sac.
Dans ce contexte, on appelle « tirage » la liste ordonnée des trois numéros obtenus.
Par exemple, si le joueur pioche le jeton numéro 4, puis le jeton numéro 5, puis le jeton numéro 1, alors le tirage correspondant est $(4;~5;~1)$.

1. Déterminer le nombre de tirages possibles.
2. 1. Déterminer le nombre de tirages sans répétition de numéro.
   2. En déduire le nombre de tirages contenant au moins une répétition de numéro.

On note $ X_1 $ la variable aléatoire égale au numéro du premier jeton pioché, $ X_2 $ celle égale au numéro du deuxième jeton pioché et $ X_3 $ celle égale au numéro du troisième jeton pioché.
Puisqu’il s’agit d’un tirage avec remise, les variables aléatoires $ X_1 $, $ X_2 $, et $ X_3 $ sont indépendantes et suivent la même loi de probabilité.

3. Établir la loi de probabilité de la variable aléatoire $ X_1 $.
4. Déterminer l’espérance de la variable aléatoire $ X_1 $.

On note $ S = X_1 + X_2 + X_3 $ la variable aléatoire égale à la somme des numéros des trois jetons piochés.

5. Déterminer l’espérance de la variable aléatoire $ S $.
6. Déterminer $ P(S = 24) $.
7. Si un joueur obtient une somme supérieure ou égale à 22, alors il gagne un lot.
   1. Justifier qu’il existe exactement 10 tirages permettant de gagner un lot.
   2. En déduire la probabilité de gagner un lot.