
Les exercices
Deux classes du collège ont répondu à la question suivante :
« Combien de livres avez-vous empruntés durant les 12 derniers mois ? »
Les deux classes ont communiqué les réponses de deux façons différentes :
| Classe n˚1 | 1; 2; 2; 2; 2; 3; 3; 3; 3; 3; 3; 3; 3; 6; 6; 6; 6; 6; 7; 7; 7 |
| Classe n˚2 |
Effectif total: 25 Moyenne: 4 Étendue: 8 Médiane: 5 |
- Comparer les nombres moyens de livres empruntés dans chaque classe.
- Un « grand lecteur » est un élève qui a emprunté 5 livres ou plus.
Quelle classe a le plus de « grands lecteurs » ? - Dans quelle classe se trouve l’élève ayant emprunté le plus de livres?
Une entreprise de transport teste une nouvelle ligne de bus quotidienne entre Lyon et Marseille pendant deux semaines.
Ce bus peut accueillir jusqu'à 50 passagers. L'entreprise vise une moyenne de passagers supérieure à 75 % de la capacité maximale du bus.
Voici le nombre de passagers par jour au cours des deux semaines :
| L | Ma | Me | J | V | S | D | |
| Semaine 1 | 34 | 41 | 37 | 40 | 48 | 50 | 43 |
| Semaine 2 | 30 | 38 | 36 | 39 | 44 | 47 | 41 |
- L’objectif a-t-il été atteint?
- Après avoir calculer la moyenne et la médiane de chaque semaine, peut-on conclure quelle semaine à été la plus performante?
Un professeur de SVT demande aux 29 élèves d’une classe de sixième de faire germer des graines de blé chez eux.
Le professeur donne un protocole expérimental à suivre :
- mettre en culture sur du coton dans une boîte placée dans une pièce éclairée, de température entre 20˚ et 25˚C ;
- arroser une fois par jour ;
- il est possible de couvrir les graines avec un film transparent pour éviter l'évaporation de l'eau.
Le tableau ci-dessous donne les tailles des plantules (petites plantes) des 29 élèves à 10 jours après la mise en germination.
| Taille en cm | 0 | 8 | 12 | 14 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| Effectif | 1 | 2 | 2 | 4 | 2 | 2 | 3 | 3 | 4 | 4 | 2 |
- Combien de plantules ont une taille qui mesure au plus 12 cm?
- Donner l'étendue de cette série.
- Calculer la moyenne de cette série. Arrondir au dixième près.
- Déterminer la médiane de cette série et interpréter le résultat.
- On considère qu'un élève a bien respecté le protocole si la taille de la plantule à 10 jours est supérieure ou égale à 14 cm.
Quel pourcentage des élèves de la classe a bien respecté le protocole ? - Le professeur a fait lui-même la même expérience en suivant le même protocole. Il a relevé la taille obtenue à 10 jours de germination.
Prouver que, si on ajoute la donnée du professeur à cette série, la médiane ne changera pas.
Le diagramme en bâtons ci-dessous nous renseigne sur le nombre de buts marqués lors de la seconde édition de la coupe de l’Outre-Mer de football en 2010. Nombre de buts marqués par ligue
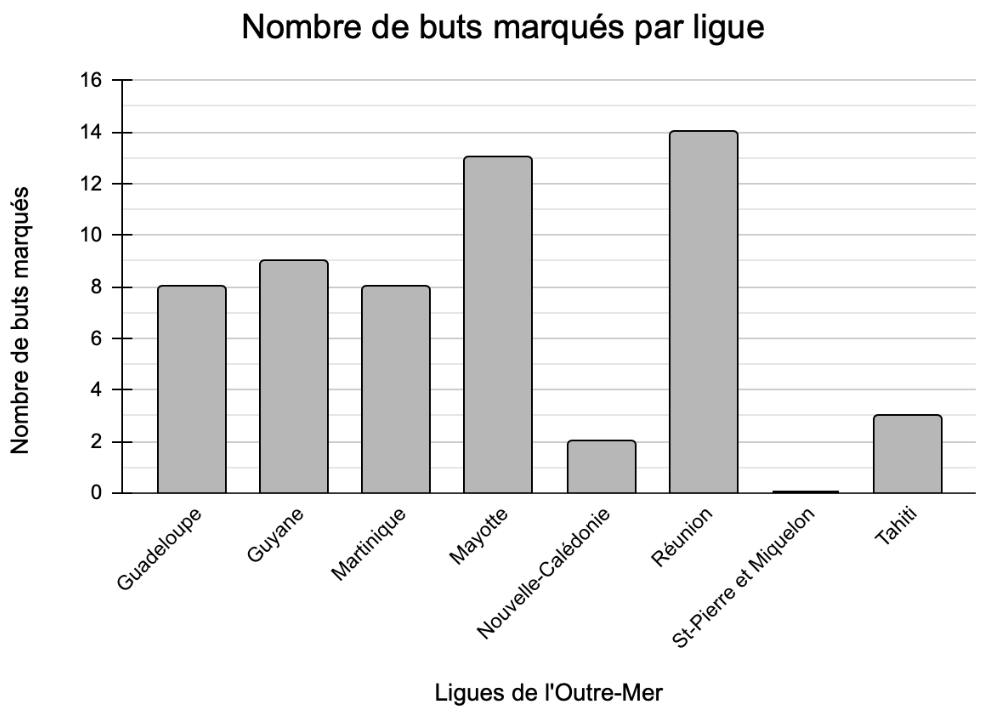
- Combien de buts a marqué l’équipe de Mayotte?
- Quelle est l’équipe qui a marqué le plus de buts?
- Quelle(s) équipe(s) ont marqué strictement moins de 8 buts?
- Quelle(s) équipe(s) ont marqué au moins 10 buts?/li>
- Quel est le nombre total de buts marqués lors de cette coupe de l’Outre-Mer 2010?
- Calculer la moyenne de buts marqués lors de cette coupe de l’Outre-Mer 2010.
- Compléter les cellules B2 à B10 dans le tableau ci-dessous.
- Parmi les propositions suivantes, entourer la formule que l’on doit écrire dans la cellule B10 du tableau pour retrouver le résultat du nombre total de buts marqués.
- Écrire dans la cellule B11 du tableau précédent une formule donnant la moyenne des buts marqués.
| A | B | |
| 1 | Ligues de l’Outre Mer | Nombre de buts marqués |
| 2 | Guadeloupe | |
| 3 | Guyane | |
| 4 | Martinique | |
| 5 | Mayotte | |
| 6 | Nouvelle-Calédonie | |
| 7 | Réunion | |
| 8 | Saint Pierre et Miquelon | |
| 9 | Tahiti | |
| 10 | TOTAL | |
| 11 | Moyenne |
| $8+9+8+13+2+14+0+3$ | $=\text{TOTAL(B2 :B9)}$ | $=\text{SOMME(B2 :B9)}$ |
Voici le classement des médailles d’or reçues par les pays participant aux jeux olympiques pour le cyclisme masculin (Source : Wikipédia).
Bilan des médailles d’or de 1896 à 2008
| Nation | Or |
| France | 40 |
| Italie | 32 |
| Royaume-Uni | 18 |
| Pays-Bas | 15 |
| États-Unis | 14 |
| Australie | 13 |
| Allemagne | 13 |
| Union soviétique | 11 |
| Belgique | 6 |
| Danemark | 6 |
| Allemagne de l’Ouest | 6 |
| Espagne | 5 |
| Allemagne de l’Est | 4 |
| Nation | Or |
| Russie | 4 |
| Suisse | 3 |
| Suède | 3 |
| Tchécoslovaquie | 2 |
| Norvège | 2 |
| Canada | 1 |
| Afrique du Sud | 1 |
| Grèce | 1 |
| Nouvelle-Zélande | 1 |
| Autriche | 1 |
| Estonie | 1 |
| Lettonie | 1 |
| Argentine | 1 |
- Voici un extrait du tableur:
Quelle formule a-t-on saisie dans la cellule O2 pour obtenir le nombre total de pays ayant eu une médaille d’or ?
A B C D E F G H I J K L M N O 1 Nombre de
médailles d'or1 2 3 4 5 6 11 13 14 15 18 32 40 2 Effectif 8 2 2 2 1 3 1 2 1 1 1 1 1 26 -
- Calculer la moyenne de cette série (arrondir à l’unité).
- Déterminer la médiane de cette série.
- En observant les valeurs prises par la série, donner un argument qui explique pourquoi les valeurs de la moyenne et de la médiane sont différentes.
- Pour le cyclisme masculin, 70 % des pays médaillés ont obtenu au moins une médaille d’or. Quel est le nombre de pays qui n’ont obtenu que des médailles d’argent ou de bronze (arrondir le résultat à l’unité) ?



